다음으로 Chapter 4를 정리해 봅니다.

Chapter 4.1 지역 변수, 범위, 지속시간
이번 챕터는 변수의 범위에 대한 내용들입니다.
namespace work1
{
int a = 1;
void doSomething()
{
a += 3;
}
}
namespace work2
{
int a = 1;
// 이름은 같은데 하는 일이 다른 경우(파라미터까지 다 같음)
// 이름이 같은데 파라미터가 다른 경우는 다른 함수로 인식해서 다른 함수로 인식.
void doSomething(int b)
{
a += 5;
}
}
int main()
{
using namespace std;
int apple = 5;
cout << apple << endl;
// apple을 선언한 이후로는 apple을 볼 수 있다. scope를 알 수 있음.
// main문 밖에서는 사용할 수 없다.
// 중괄호가 끝나면 메모리가 이미 반납되어서 apple이라는 변수는 없다.
// apple = 1;
// nested block
// 밖에서 정의된 변수는 block 안쪽에서 볼 수도 있고 사용할 수도 있다.
{
// 만약 int apple = 1;로 정의하면 밖에 있는 apple하고 다름.
// 이름이 같더라도 더 적은 영역에 있으면 기존 apple이 사라짐 (name hiding), 이름은 같지만 완전히 다름.
// 따라서 가급적 변수 이름은 범위가 다르더라도 다르게 짓는 것이 좋음.
apple = 1;
cout << apple << endl;
}
// 현대적 프로그래밍에서는 변수가 살아남는 범위를 줄이려고 함.
// 따라서 변수가 사용되는 곳 근처에서만 살아남도록 최소한의 범위를 갖도록 블럭으로 만들어줌.
// 범위를 쪼개고 쪼개는게 객체지향 프로그래밍의 기본적인 철학.
cout << apple << endl;
// :: 연산자는 영역/범위 결정 연산자. Scope resolution operator
// 이름이 충돌할 때 이를 해결하기 위해서 이름 공간을 쪼갠다.
// C++17 에서는 nested namespace 지원함.
work1::a;
work1::doSomething();
work2::a;
work2::doSomething(3);
}
주석으로 내용을 정리해 두었는데, 글로 한 번만 더 정리해 보자면,
- 중괄호가 끝나면 메모리가 반납되며 변수는 제거됨. (변수의 범위와 지속시간)
- block 밖에서 정의된 변수는 block 안쪽에서 볼 수도 있고 사용도 가능.
- 만약 block 안에서 같은 자료형과 같은 변수명으로 다시 한번 선언하는 경우, block 밖에 있던 변수와는 별개.
- 범위가 다르더라도 혼동을 줄이기 위해 변수명은 다르게 지어야 한다.
- 변수 이름으로 충돌하는 경우를 해결하기 위해 namespace 기능을 사용함.
Chapter 4.2 전역 변수, 정적 변수, 내부 연결, 외부 연결
- 지역 변수(Local variable): Linkage가 없으며, Linking 시 고려하지 않음.
- 내부 연결(Internal linkage): 한 파일 안에서는 어디서든 사용할 수 있음.
- 외부 연결(External linkage): cpp 파일이 여러 개 있을 때, 한 cpp 파일에서 선언한 변수를 다른 cpp에서도 사용할 수 있음.
예시 코드 1
int value = 123;
int main()
{
std::cout << value << std::endl;
int value = 1;
std::cout << value << std::endl;
// Global scope operator
std::cout << ::value << std::endl; // 영역 연산자, 다른 영역에 정의된 변수를 사용하는 것.
}

main문 안에서 value가 선언되기 전에 cout으로 호출하게 되면 밖에서 이미 선언된 변수의 값을 가져온다.
main문 안에서 value가 선언된 후에는 cout으로 호출했을 때 내부에 선언된 변수 값을 가져온다.
만약 밖에서 선언된 변수의 값을 출력하고 싶다면, ::를 활용한다.
예시 코드 2
void doSomething()
{
// static? c를 만든 사람 입장에서 봐야한다...
// 변수 a가 os로부터 받은 메모리가 static이다.
// 이 영역 안에 변수가 선언될 때 같은 메모리를 사용한다. 두번, 세번 실행되더라도 같은 메모리 사용. 초기화를 한번만 함.
// static 변수는 반드시 한 번은 초기화를 해줘야함. (메모리에 얹어줘야하기 때문에)
// 함수를 몇 번 호출되는지 확인해볼 때 사용. 디버깅에서 쓴다.
static int static_a = 1;
int a = 1; // 계속 메모리를 새로 할당받음.
a++;
static_a++;
std::cout << "a: " << a << std::endl;
std::cout << "static_a: " << static_a << std::endl;
}
int main()
{
doSomething();
doSomething();
doSomething();
doSomething();
}
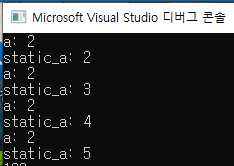
다음은 static 변수에 대한 설명이다.
static이라는 것은 os로부터 받은 메모리가 static이라는 얘기이다. 즉, 이 영역 안에서 변수가 선언될 때 같은 메모리를 사용한다. 2번, 3번 실행되더라도 같은 메모리를 사용하게 되며, 초기화는 한 번만 한다.
따라서 static 변수는 반드시 한 번은 초기화를 해줘야한다는 특징이 있다.
반면 static int가 아닌, 일반 int를 사용하면 계속 초기화를 해주기 때문에 값이 같은 것을 확인할 수 있다.
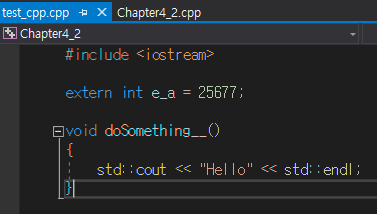
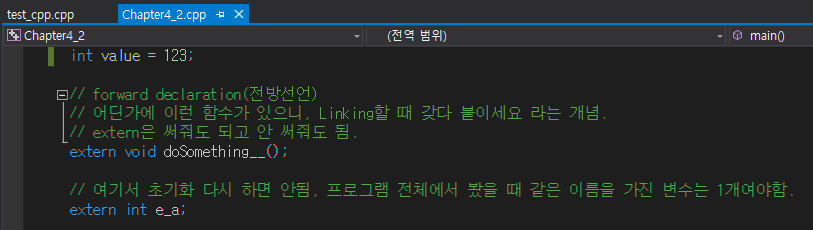
여러 cpp 파일에서 사용할 수 있는 방법은 바로 extern을 붙이는 것이다.
test_cpp.cpp라는 파일에서 선언된 int e_a는 Chapter 4_2.cpp라는 파일에서도 사용할 수 있는데, 이는 extern int e_a로 선언했기 때문이다.
함수 또한 다른 cpp 파일에서 정의된 것을 사용할 수 있는데, 이는 전방선언을 활용하면 된다. 단 함수의 경우 extern이 필수는 아니다.
만약 내가 여러 cpp 파일에서 사용할 상수가 있다고 가정하자.
그럼 어떻게 해야 효율적으로 상수를 정의해서 사용할 수 있을까?
// my_constant.h
namespace Constants
{
extern const double pi = 3.14;
extern const double gravity = 9.8;
}
// test_1.cpp
#include "my_constant.h"
int main() {
std::cout << &Constants::pi << std::endl;
return 0;
}
// test_2.cpp
#include "my_constant.h"
int main() {
std::cout << &Constants::pi << std::endl;
return 0;
}
위 코드처럼, 만약 헤더파일에 extern const 변수를 선언하게 되면, 각각의 cpp에서 해당 변수를 사용할 때 메모리가 각각 사용된다.
안타깝게도 강의에서는 자세히 언급을 해주시지 않아서, 제미나이를 활용해 보았더니 다음과 같은 대답을 얻을 수 있었다.

헤더 파일에 extern const로 변수를 선언하는 경우, 컴파일러에 의해서 번역될 때 각 cpp 파일에 별도의 변수 인스턴스를 만들도록 지시한다고 한다.
따라서 이를 방지하려면, 헤더 파일에서는 변수 선언만 하고, 값을 선언하는건 별도의 cpp 파일을 만들어서 해줘야 한다.
// Constants.h
namespace Constants
{
extern const double pi;
extern const double gravity;
}
// Constants.cpp
#include "Constants.h"
namespace Constants
{
const double pi = 3.14;
const double gravity = 9.8;
}
// test_1.cpp
#include "Constants.h"
#include <iostream>
int main() {
std::cout << &Constants::pi << std::endl;
return 0;
}
// test_2.cpp
#include "Constants.h"
#include <iostream>
int main() {
std::cout << &Constants::pi << std::endl;
return 0;
}
다음과 같이, 별도의 cpp 파일에서 값을 제공해주는 방식으로 하면 다른 cpp 파일에서 해당 변수 사용 시 주소가 같다.

Chatper 4.3 Using문과 모호성
예시 코드 1
namespace a
{
int my_var(10);
}
namespace b
{
int my_var(20);
}
int main()
{
using namespace a;
using namespace b;
std::cout << my_var << std::endl; // 모호하다는 에러 발생
std::cout << a::my_var << std::endl;
std::cout << b::my_var << std::endl;
}
namespace a와 namespace b 모두에 my_var라는 int 변수가 있는 경우, using namespace a, b 모두를 사용하면 my_var이 a에 있는 걸 써야 할지, b에 있는 걸 써야 할지 몰라서 모호하다는 에러가 발생한다.
가장 명확하게 해결하는 방법은, :: 연산자를 활용해 어떤 namespace에 있는 변수인지를 명시적으로 알려주는 것이다.
예시 코드 2
namespace a
{
int my_var(10);
}
namespace b
{
int my_var(20);
}
int main()
{
using namespace b;
{
using namespace a;
std::cout << my_var << std::endl; // a와 b 영향을 다 받는다, 모호함 해결 X
}
std::cout << my_var << std::endl; // namespace b로 사용됨.
}
블록으로 따로 영역을 잡아주고, using namespace a를 적용해주는 경우, 블록 안에 있는 my_var는 여전히 using이 두 개 적용 되는 상황이므로 모호성이 해결되지 않는다.
단, 블록 바깥쪽에 있는 my_var는 b의 my_var로 적용된다.
예시 코드 3
namespace a
{
int my_var(10);
}
namespace b
{
int my_var(20);
}
int main()
{
{
using namespace a;
std::cout << my_var << std::endl;
}
{
using namespace b;
std::cout << my_var << std::endl;
}
}
블록으로 영역을 따로 따로 잡아주면, 모호성이 없어진다.
using namespace를 특정 헤더에서 전역 범위에 넣어버리면, 헤더를 include 하는 모든 cpp 파일에 영향을 주게 된다.
따라서 가급적이면 cpp 파일에 넣는 방향이 좋다.
using namespace std처럼 큰 범위에 적용하는 using을 사용하는 경우, 다른 namespace에서 std에 들어간 함수명과 겹치는 이름의 변수를 사용하려고 할 때 선택을 해야 한다. using namespace std를 포기할지, 혹은 using namespace a를 포기할지. 강의에서는 count라는 변수를 통해서 예시를 보여주셨는데, std::count라는 함수가 있어서 namespace에 count라는 이름으로 변수를 사용하게 되면 겹치게 되어 문제가 발생하는 것을 확인할 수 있었다.
Chapter 4.4 auto 키워드와 자료형 추론
예시 코드 1
// Parameter에는 auto 사용 불가.
auto add(int x, int y) -> int
{
return x + y;
}
int main()
{
using namespace std;
// 자료형을 상황에 따라서 결정하게 만드는 것을 형 추론이라고 한다. auto 키워드 사용.
// 값을 주지 않으면 사용할 수 없음.
// 계산 결과가 어떻게 나오는지 인지하고 있어야 함.
auto a(123); // int
auto d(123.0); // double
auto c(1 + 2.0); // double
// 함수의 return 값에도 auto 사용 가능.
auto result = add(1, 2);
}
자료형을 상황에 따라 결정하게 만드는 것을 형 추론이라고 하는데, 이는 auto 키워드를 사용한다.
예를 들어서, auto a(123); 라고 하면 값이 int 이므로 a는 int로 결정이 된다.
auto d(123.0); 라고 하면 값이 소수점이므로 d는 double로 결정이 된다.
함수의 return type에도 auto를 사용할 수 있고, 함수의 return을 받는 변수도 auto를 사용할 수 있다.
함수의 return type을 auto로 하더라도, 명시적으로 자료형을 표기하고 싶다면 ->를 사용해서 표현할 수 있다.
auto func() -> int 로 만드나, int func()로 만드나 같지만, 여러 함수가 있을 때 각 함수의 return type을 한눈에 보기에는 전자를 사용하는 것이 더 좋다.
Chapter 4.5 형변환 (Type conversion)
예시 코드 1
#include <iostream>
#include <typeinfo>
cout << typeid(4).name() << endl;
cout << typeid(a).name() << endl;
typeinfo를 include하면, typeid라는 함수를 사용할 수 있는데, 이는 자료형을 알려주는 함수이다.
auto를 사용하는 경우라던가, 변수의 자료형을 알 수 없는 경우 유용하게 사용할 수 있다.
예시 코드 2
// 메모리를 작게 사용하는 데이터 타입을 메모리를 크게 사용하는 데이터 타입으로,
// numeric promotion, 암시적 형변환 사용
float a = 1.0f;
double d = a;
다음으로는 numeric promotion에 대한 설명이다.
2
메모리를 작게 사용하는 데이터 타입(float)를 메모리를 크게 사용하는 데이터 타입(double)으로 변경하는 경우를 말한다. 이런 경우는 명시적인 형변환이 아닌, 암시적인 형변환을 사용한다는 특징이 있다.
적은 메모리에서 큰 메모리로 형변환이 되기 때문에, 값의 변경 없이 type만 변경된다.
예시 코드 3
// numeric conversion
double dd = 3; // int를 double로, 타입이 바뀌는 경우
short s = 2; // int를 short로, 큰 자료형을 작은 자료형으로 보내는 경우
// numeric conversion issue
int i = 30000;
char c = i;
// issue 2
double d_ = 0.123456789;
float f_ = d_;
// unsigned라서 제대로 저장될 수 없는 경우
// 자료형의 우선순위가 int가 가장 낮고, unsigned int,
// long, unsigned long, long long, unsigned long long, float, double, long double 순이다.
// unsigned가 우선순위가 더 높으니 int로 바꾸지 않는 경우임. (주의!)
cout << 5u - 10u;
다음은 numeric conversion에 대한 설명이다.
int를 double로 바꾸는 것 처럼, data type 자체가 변하는 경우가 있으며
int를 short로, 즉 큰 자료형을 작은 자료형으로 보내는 경우가 있다.
이런 경우에 문제가 발생할 수 있는데, 예를 들어 int i = 30000;로 정의했는데 char 타입으로 받게 되면 char 타입의 자료형 크기를 초과하므로 c의 값은 정상적으로 i 값을 받아올 수 없다.
마찬가지로 double 자료형의 변수를 float로 받는 경우, 정밀도의 차이가 있어 double 변수의 값을 온전히 float 변수가 받을 수 없다.
그리고 자료형의 우선순위 문제로, 5u(숫자 5이나, unsigned int를 의미함) - 10u는 실제로 -5 값으로 나와야 하나, 우선순위 상 unsigned int가 더 높기 때문에 이를 signed int 형태인 -5로 표현하지 않고 이상한 값으로 표현하게 된다. 이런 경우 우리가 기대하는 값과 전혀 다른 값이 들어갈 수 있기 때문에 주의해야 한다.
Chatper 4.6 문자열 std string 소개
해당 강의에서는 문자열을 표현하는 자료형인 std::string에 대해서 소개한다.
예시 코드 1
#include <string>
int main()
{
// char하고 string하고 색이 다르다.
// C++에서 기본적으로 제공해주는건 한 글자다.
// 한 글자를 여러개 나열하는 방식으로 문자열을 사용한다.
// char가 기본적으로 사용하는 방식
const char my_strs [] = "Hello, World";
// 프로그래머들이 편하라고 제공하는 방식.
// 프로그래머들이 문자를 다룰 때 많이 사용하는 것들을 string 안에 미리 구현해뒀음.
// 일종의 사용자 정의 데이터 타입이라고 보면 됨. 기본 자료형처럼 쓸 수 있는데 추가적인 기능이 들어가있는 것.
const string my_hello = "Hello, World";
string my_ID = "123";
cout << my_strs << endl;
C++에서 제공하는 기본적인 자료형은 char이나, 문자를 조금 더 편하게 다룰 수 있도록 만들어진 것이 std::string 자료형이라고 이해하면 된다고 한다.
그렇다 보니, const char는 글자색이 같은데, string은 색이 다르다. string은 기본 자료형이 아니며, 일종의 사용자 정의 데이터 타입이라고 볼 수 있다.
예시 코드 2
cout << "Your name ? : ";
string name;
//cin >> name;
std::getline(std::cin, name);
cout << "Your age ? : ";
string age;
std::getline(std::cin, age);
cout << "My name is: " << name << " My age is : " << age << endl;
일반적으로 데이터를 입력받는다고 하면 cin을 사용하면 된다.
그러나, cin을 사용할 때 한 칸을 띄어버리게 되면 두 개의 cin으로 나눠서 들어가게 된다.
예를 들어서,

cin을 사용할 때는 한 칸을 띄우게 되면 happy는 앞 cin에, cat은 그다음 cin으로 들어가게 되어서 두 번째 cin에는 입력을 할 수 없으며 자동적으로 할당을 하게 된다.
따라서 이를 방지하려면 std::getline을 사용하여 cin을 받아야한다.
예시 코드 3
cout << "Your age ? : ";
int age;
cin >> age;
// \n이 만날 때 까지 글자를 무시하라
//std::cin.ignore(std::numeric_limits<std::streamsize>::max() , '\n');
cout << "Your name ? : ";
string name;
std::getline(std::cin, name);
cout << "My name is: " << name << " My age is : " << age << endl;
이번에는 이전과 달리, int를 입력받고 string을 입력 받으려고 하는 경우이다.
int를 입력 받으려면 cin을 사용해야 하므로, cin으로 age를 받고 다음은 문자열을 받기 위해 getline을 사용하려고 하였다.
하지만 cin을 사용해서 입력한 후 엔터 키를 누르면 입력 버퍼에 \n가 남아있어서 이를 getline에서 읽고 빈 문자열을 name에 할당한 후 종료하게 되는 문제가 있다.
따라서 이를 해결하려면 cin.ignore를 적용하여 글자를 무시하도록 적용해줘야 한다.
예시 코드 4
string a = "Hello, "; // 마우스를 대보면 [8]로 나오는데, 이는 문자열이 8개라는 의미. 하지만 실제로는 7개, 맨 마지막에 널 캐릭터가 숨어 있음.
string b = "World";
string hw = a + b;
hw += " Good";
//cout << hw << endl;
cout << hw.length() << endl; // string 길이 확인.
다음은 string을 + 연산자를 활용해서 붙이는 경우를 보여준다.
string a 하고 string b를 + 연산자로 붙이면, 그대로 문자열이 붙게 된다.
그리고 문자열의 길이를 확인할 때는 .length()를 활용하면 된다.
조금 특이한 점은, string a의 경우 "Hello, "이니까 실제로는 7글자인데, 마우스 커서를 대보면 const char [8]로 나온다. 이는 맨 마지막에 널 캐릭터가 숨어져 있기 때문이며, C 스타일 문자열은 항상 널 캐릭터로 끝나야 하는 규칙이 있다. 이를 통해 문자열의 끝을 확인할 수 있는 것이다.
Chatper 4.7 열거형 (enumerated types)
이번 강의에서는 enum 이라고 하는 자료형인 열거형에 대해서 다룬다.
// 사용자 정의 자료형 (user-defined data types)
enum Color
{
COLOR_BLACK, // -3으로 지정나면 나머지들은 +1씩 값으로 지정됨.
COLOR_RED,
COLOR_BLUE,
COLOR_GREEN,
}; // ; 없으면 빌드 에러남.
enum Feeling
{
HAPPY,
JOY,
TIRED,
BLUE
};
Color my_color = COLOR_RED;
int color_id = COLOR_RED;
일단 enum의 특징은, 처음 값을 0으로 시작해서 1씩 증가하도록 설계되어 있다. COLOR_BLACK이 0이고, COLOR_RED가 1이고 이런 식이다.
기본적으로는 그렇지만, 만약 수동으로 값을 지정해 주면, 값이 달라지나 규칙은 유지된다.
예를 들어 맨 처음 값을 -3으로 주면 그다음 값은 -2, -1, 0이 되는 것이다.
enum 사용 시 맨 마지막에 괄호 닫고 ;를 꼭 써줘야만 빌드에 문제가 없다.
그리고 다른 enum이더라도 만약 안에 사용하는 요소의 이름이 같으면 문제가 생긴다. 따라서 이름은 항상 다르게 지어주어야 한다.
COLOR_RED는 Color라는 이름의 자료형인 my_color에 사용할 수도 있고, int형 변수에도 사용할 수 있다. cout으로 출력하면 정상적으로 1로 출력이 된다.
그리고 여러 cpp 파일에서 enum을 공동으로 사용하는 경우가 많기 때문에, 헤더파일에 enum을 정의해 두고 각. cpp에서 #include 형식으로 헤더 파일을 읽어오게 만들어주면 유용하게 사용할 수 있다고 한다.
Chapter 4.8 영역 제한 열거형 (열거형 클래스)
해당 강의에서는 이전 강의에서 배웠던 열거형 자료형에서 변화한 형태인 열거형 클래스에 대해서 다루게 된다.
예시 코드 1
enum Color
{
RED,
BLUE
};
enum Fruit
{
BANANA,
APPLE
};
Color color = RED;
Fruit fruit = BANANA;
if (color == fruit)
{
cout << "Color == fruit";
}
우선 저번 강의 때 배웠던 열거형 type을 그대로 사용해 보자.
열거형의 특성상 안에 있는 값들을 int로 사용한다.
따라서 Color 자료형의 RED와 Fruit 자료형의 BANANA는 동일하게 int로는 0이다.
그래서 if 문에서도 같다고 판단을 하게 된다.
이런 경우 int 값으로는 같으나 실제 데이터는 다른 상황이니, 실수할 가능성을 만들 수 있다.
이를 방지하고자 사용하는 것이 enum class이다.
예시 코드 2
using namespace std;
enum class Color
{
RED,
BLUE
};
enum class Fruit
{
BANANA,
APPLE
};
Color c_1 = Color::RED;
Color c_2 = Color::BLUE;
if (c_1 == c_2)
{
cout << "same color! " << endl;
}
enum과 다른 점은, enum class에서 사용된 멤버는 enum 때처럼 그냥 사용할 수 없고, 마치 namepsace처럼 ::를 사용해야 한다.
그래서 기존하고 다르게 Color::RED 이런 식으로 사용해야 한다.
그리고 enum 때와 다르게 만약 Fruit 자료형 변수를 사용할 경우 == 연산자 자체를 사용할 수가 없다.
강의를 듣고 나서 약간 헷갈리는 부분들이 있어서, Gemini를 활용해 정리를 요청했더니 조금 더 깔끔하게 정리된 것 같다.
해당 내용을 첨부하니, 정리용으로 보면 좋을 듯하다.
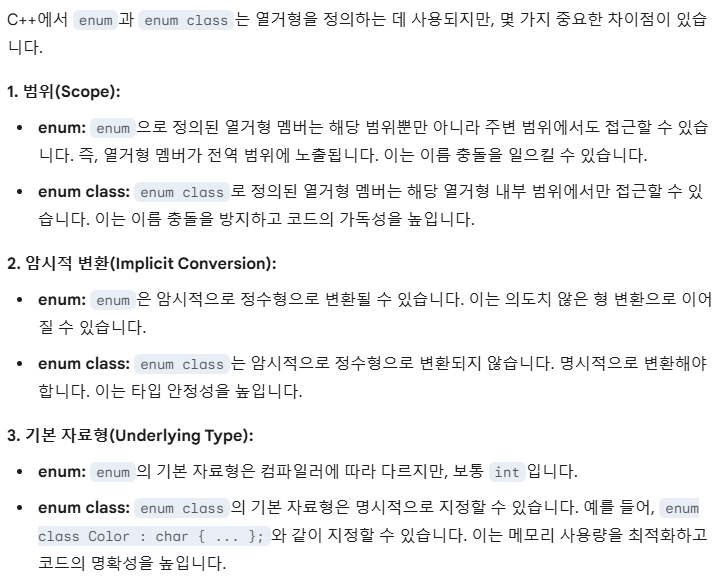

enum을 수업할 때 언급된 내용도 있고 아닌 내용도 있는데 한번 정리해 보자면...
우선 Scope가 다른데, 이전 enum 수업에서도 언급이 나왔다시피 enum 안에 멤버로 선언된 변수는 다른 범위에서도 접근이 가능하다. 그래서 서로 다른 enum 끼리 같은 멤버를 쓰면 안 된다는 내용이 수업시간에 나왔었다. 마치 전역 변수처럼 사용되기 때문이다.
그런데 enum class의 경우 namespace처럼 범위가 한정되기 때문에 이런 문제가 발생하지 않는다.
다음으로는 암시적 변환에 대한 부분인데... enum에 사용된 멤버는 암시적으로 형 변환이 된다. 특히 enum의 멤버는 int 값으로 저장이 되고 있기 때문에... 이를 int로 형변환 할 수 있다.
하지만 enum class의 경우 static_cast <int>를 통해서 명시적 형변환을 해줘야만 int로 변환이 가능하다. 이런 관점에서는 enum class가 훨씬 안전하다고 볼 수 있겠다.
그리고 자료형에 대해서는, enum의 경우 보통 int로 사용되나 enum class는 자료형을 명시적으로 지정할 수 있다고 한다. 이 내용은 수업시간에 나오진 않았던 내용인데 이런 기능을 보니 확실히 enum보다는 enum class가 더 많이 쓰이는 이유를 알 수 있을 듯하다.
namespace의 경우 이미 잘 아는 내용이고... 비교에 대해서도 앞의 예제에서 언급했듯이 다른 enum class 끼리는 비교 연산자가 작동하지 않는다. (에러가 발생함)
Chapter 4.9 자료형에게 가명 붙여주기
해당 강의에서는 자료형에 새로운 이름을 붙여서 사용하는 방식인 typedef에 대해서 다룬다.
#include <iostream>
#include <cstdint>
#include <vector>
int main()
{
typedef double distance_t; // 코드상에서 둘 다 사용 가능함. 보통 뒤에는 _t는 타입 이름이다 라는 의미.
double my_distance;
distance_t home2work;
distance_t home2school;
// aliases를 사용하는 이유에 가까움.
//typedef std::vector<std::pair<std::string, int>> pairlist_t;
using pairlist_t = std::vector<std::pair<std::string, int>>;
pairlist_t pairlist1;
pairlist_t pairlist2;
}
typedef의 경우 typedef 사용하고자 하는 자료형 별명 순서로 사용하게 된다
위 코드에서 distance_t라는 자료형은 실제로 double과 같은 자료형이나 이름만 붙여준 것이라고 보면 된다.
그리고 여러 자료형을 혼합해서 사용해 자료형의 이름이 길어질 때, 이를 축약해서 사용할 때도 유용하게 사용할 수 있다.
Chapter 4.10 구조체 struct
이번 강의에서는 클래스로 넘어가는 다리이자, 다양한 자료형을 하나의 바구니에 담을 수 있는 방법인 구조체에 대해서 다룬다.
예시 코드 1
#include <string>
struct Person
{
double height = 3.0;
float weight = 200.0;
int age = 100;
string name = "Hello";
// 여러 변수들을 가지고 기능을 하려고 하는 함수다.
// 데이터와 기능을 묶은 것.
void print()
{
cout << height << " " << weight << " " << age << " " << name << " ";
cout << endl;
}
};
int main()
{
Person me;
cout << me.name << endl;
Person me{ 2.0, 100.0, 20, "Jack Jack"};
me.print();
}
구조체는 여러 자료형을 한 번에 담을 수 있는 특징을 가지고 있다.
따라서 struct 안에 double float int string 등 다양한 자료형이 존재할 수 있으며, 위 코드와 같이 초기값을 주기도 한다.
그리고 신기하게 struct 안에 함수를 쓸 수도 있다.
구조체의 멤버 변수에 접근할 때는 . 을 사용하면 된다.
uniform initialization을 활용하면 조금 더 손쉽게 구조체에 값을 줄 수 있다.
예시 코드 2
struct Employee // 14 bytes
{
short id; // 2 bytes
int age; // 4 bytes
double wage; // 8 bytes
};
// 자료를 배치할 때 컴퓨터 잘 처리할 수 있는 형태로 하다보면 추가로 더 들어감. (패딩 이라고 부름)
Employee emp1;
cout << sizeof(emp1) << endl; // 16
구조체 type에도 sizeof를 사용할 수 있다.
다만, 자료를 배치할 때 컴퓨터가 잘 처리할 수 있는 형태로 하다 보면 실제 값하고는 차이가 있을 수 있다고 하니 주의해야 한다고 한다. 이를 패딩이라고 한다고 한다.
Gemini에게 물어보니, 조금 더 구체적인 답변을 들을 수 있었다.
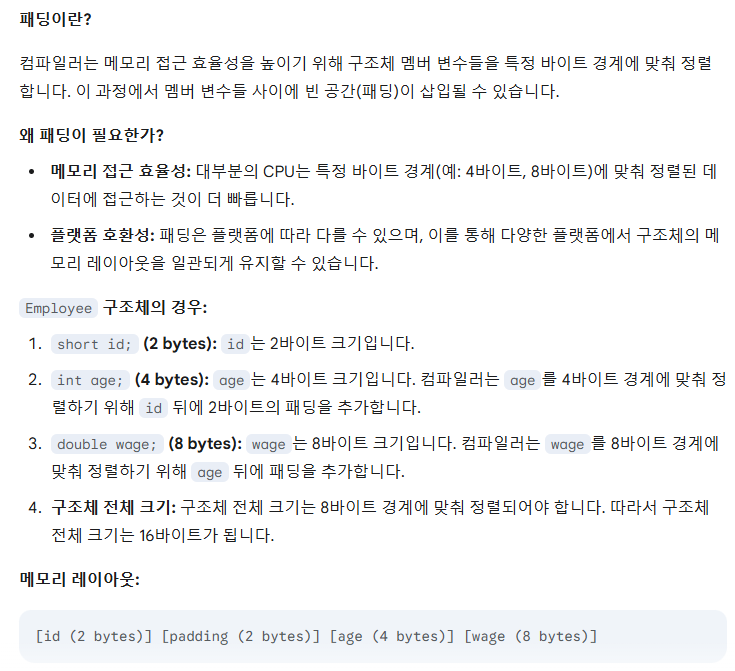
수업 시간에도 2바이트를 처리하기가 좀 어렵다? 이런 얘기를 하셨는데, Gemini의 답변을 듣고 나니 CPU가 메모리에 접근할 때 4 byte나 8 byte와 같은 경계 기준이 있는 것으로 보인다.
여기까지 Chatper 4를 모두 정리해보았다.
중간에 회사 일이 너무 바빠 퇴근을 할 수 없어, 작성이 계속 지연되었다.
다시 열심히..! 해보려고 한다
'C++ > 따라하며 배우는 C++' 카테고리의 다른 글
| 홍정모의 따라하며 배우는 C++ - Chapter 3 (0) | 2025.02.09 |
|---|---|
| C++ 공부 관련 정리글을 업로드 해보려고 합니다. (0) | 2025.02.02 |