헤헤

안녕하세요.

오늘은 Anomaly Detection 분야의 논문 중, 최근에 나온 논문으로 제가 관심 있게 본 논문이라서 논문 review를 남기고자 합니다.

대학원에 있을 때는 새로운 논문이 나오면 바로 바로바로바로 follow-up 하곤 했는데, 회사에 다니고 나니 논문을 읽는 것 외에도 워낙 할게 많으니 바로바로 따라가기는 쉽지가 않네요.

그래도 제가 가장 관심 있는 분야라 시간이 되면 틈틈히 새로운 논문들 review 해보도록 하려고 합니다.

Official 코드가 나와있지 않은 관계로, 사람들이 unofficial로 implementation 코드를 만드시는 것 같은데 어느 정도 시간이 흐르고 결과가 유사하게 나오는 시점쯤이 되면 code review도 함께 진행해 보도록 하겠습니다.

https://arxiv.org/abs/2303.14535

1. Abstract

본 논문에서, 저자들은 computational efficiency에 집중하여 현대 GPU에서 1ms 이내로 이미지를 처리할 수 있는 lightweight feature extractor를 제안합니다. 그리고 anomalous feature를 검출하기 위해 stduent-teacher approach를 사용합니다.

저자들은 정상 이미지에서 추출된 feature를 예측하는 student network를 학습시킵니다.

Test time에서 anomaly의 검출은 student network가 추출된 feature를 예측하는데 실패하는 것을 통해 진행됩니다.

저자들은 정상이 아닌 이미지에 대해서 student network가 teacher network를 따라하지 못하도록 만드는 training loss를 제안합니다. 이는 student-teacher model의 computational cost를 대폭 감소시키면서 anomalous feature를 탐지하는 능력은 향상하게 됩니다.

저자들은 추가적으로 물건이 잘못 배치되는 것과 같은 logical anomaly를 잡아내는 문제 또한 다루고 있습니다. 저자들은 이러한 문제를 이미지를 전역적으로(globally) 분석하는 autoencoder를 효율적으로 활용해 검출하게 됩니다.

2. Introduction

최근 classification architecture들은 latency, throughput, memory consumption, 학습 가능한 파라미터의 수와 같은 특성들에 초점을 두고 있습니다. 이는 network들이 real-world application에 적용할 수 있다는 것을 보장하게 됩니다.

하지만, State-of-the-art anomaly detection 방법론들은, anomaly detection 성능을 증가시키기 위해서 computational efficiency를 희생하곤 합니다. 자주 사용되는 기법으로는 앙상블, large backbone의 사용, input image의 resolution을 768x768 사이즈로 올리는 방법들이 있습니다.

Real-world anomaly detection application에서는 방법론의 computational requirement에 제약이 있는 경우들이 많은데, 이는 anomaly를 너무 늦게 찾게 되면 상당한 경제적 피해를 가지고 오기 때문입니다. 예를 들어서, 금속 물질이 경작 기계의 내부에 들어간다거나, 혹은 기계를 작동하는 사람의 신체가 칼날에 접근하는 경우가 발생할 수 있습니다.

게다가 산업 현장에서의 환경은 높은 생산률을 유지하기 위해서 엄격한 runtime limit을 가지고 있는 경우가 많습니다. 따라서, 이러한 제약을 고려하지 않게 되면 생산성 감소를 만들 수 있고, 경제적 가능성을 감소시키게 됩니다. 

그러므로, anomaly detection 방법론이 real-world에서 사용되려면 computational cost에 대해서 필수적으로 고려해야 합니다.

본 논문에서, 저자들은 anomaly detection 성능을 내면서도 inference runtime까지 동시에 고려하는, 새로운 표준이 될 방법론인 EfficientAD를 제안합니다. 

첫 번째로, modern GPU에서 1ms 이내로 expressive feature를 계산하기 위한 efficient network architecture를 도입합니다. 

두 번째로, anomalous feature를 검출하기 위해, student-teacher approach를 사용합니다.

저자들은 정상 이미지에 대해서 pretrained teacher network를 가지고 계산된 feature를 예측하는 student network를 학습합니다. Anomalous image에 대해서는 student network가 학습되지 않았기 때문에, 이러한 이미지에 대해서는 teacher network를 따라 하는 것에 실패하게 됩니다. 따라서, test time때 student network와 teacher network의 output 사이의 큰 distance를 기반으로 anomalous image를 검출하게 됩니다. 

이러한 효과를 더 증가시키기 위해서, 'Asymmetric student-teacher networks for industrial anomaly detection' 논문에서는 teacher network와 student network간 architectural asymmetry를 사용하였는데요. 저자들은 대신에, 정상 이미지가 아닌 이미지에 대해서 student network가 teacher network를 따라 하지 못하게 만드는 training loss를 도입하여 loss-induced asymmetry를 도입하였습니다. 

이 loss는 test time에서 computational cost에도 영향을 주지 않고, architecture design에 제약을 주지 않으며, anomalous feature를 정확히 검출하면서도 student network와 teacher network 모두에 efficient network architecture를 사용할 수 있게 만듭니다.

Anomalous local feature를 확인하는 것은 생산된 제품에 오염이나 얼룩과 같이, 정상 이미지와 구조적으로 다른(structurally different) anomaly를 검출하게 합니다. 하지만, 어려운 문제는 정상 이미지의 position, size, arrangement와 관련된 logical constraint에 대한 이상 여부를 찾아내는 것입니다. 이러한 문제를 해결하고자, EfficientAD는 'Beyond Dents and Scratches: Logical Constraints in Unsupervised Anomaly Detection and Localization' 논문에서 제안된 autoencoder를 사용합니다. 이 autoencoder는 test time에서 학습 이미지의 logical constraint를 학습하고, violation을 탐지하게 됩니다.

저자들은 autoencoder의 구조와 학습 protocol을 단순화 하면서, 어떻게 이를 student-teacher model과 효율적으로 통합할 수 있는지를 논문에서 설명합니다. 또한, autoencoder와 student-teacher model의 detection result를 합치기 전에 보정해서 anomaly detection 성능을 향상할 수 있는 방법 또한 제안합니다.

저자들의 contribution은 다음과 같이 요약해볼 수 있습니다.

- 이미지 한 장당 2ms 이내의 latency를 보여주면서, industrial benchmark에 대해서 anomaly detection과 localization에서 SOTA 대비 상당히 성능을 향상했습니다.

- 최근 anomaly detection 방법론들과 비교했을 때 feature extraction의 속도를 몇 배 향상할 수 있는 efficient network architecture를 제안합니다.

- Inference runtime에 영향을 미치지 않으면서 student-teacher model의 이상 탐지 성능을 상당히 향상시킬 수 있는 training loss를 도입합니다.

- autoencoder 기반으로 효율적으로 logical anomaly를 검출하고, student-teacher model의 검출 결과와 통합한 후 보정할 수 있는 방법을 제안합니다.

3. Related Work

3.1 Anomaly Detection Tasks

간단한 내용이라서, 해당 글에서는 생략하겠습니다. 

3.2 Anomaly Detection Methods

전통적인 컴퓨터 비전 알고리즘은 수십 년간 산업용 이상 탐지 문제에 성공적으로 적용되어 왔습니다. 이러한 알고리즘들은 흔히 이미지 한 장당 몇 ms 이내에 이미지를 처리해야 하는 요구사항을 충족해 왔습니다. Bergmann는 이러한 방법론들을 평가해 보았고, 사물이 똑바로 위치해있지 않은 경우에는 실패한다는 것을 확인하였습니다.

딥러닝 기반의 방법론들은 이러한 케이스에서도 강건하게 작동한다는 것을 보여왔습니다. 최근에 성공적인 방법론들은 pretrained 되고 frozen 된 CNN의 feature space에서 밀도 추정을 하거나 outlier를 검출합니다. 만약 feature vector가 input pixel에 매핑될 수 있다면, 이들의 outlier score를 각각의 pixel에 할당해서 2D anomaly map을 만들 수 있게 됩니다.

최근 방법들은 다변량 정규 분포, Gaussian Mixture Models, Normalizing Flow, kNN 알고리즘을 사용하곤 합니다. kNN은 Nearest Neighbor를 찾는 것에 있어서 runtime을 많이 잡아먹게 되는데, PatchCore는 이를 해결하고자 군집된 feature vector들의 reduced database를 만들어서 여기서만 kNN을 진행하도록 합니다. 

Bergmann은 이상 탐지를 위한 student-teacher (S-T) framework를 제안하였습니다. 여기서 teacher network는 pretrained frozen CNN입니다. 해당 연구에서는 3가지 다른 receptive field 크기를 가진 teacher network를 사용합니다. 각 teacher network는 학습 이미지에서 teacher network의 output을 따라 하는 3개의 student network를 학습시킵니다. 

student network는 이상이 있는 이미지를 학습하는 동안에 본 적 없기 때문에, 이들에 대해서는 teacher network의 output을 예측하는 것에 실패하기 때문에 이를 기반으로 이상 탐지가 가능합니다. Bergmann은 student network의 output의 variance와 teacher network의 output 간의 distance를 가지고 anomaly score를 계산하였습니다. 

S-T framework의 다양한 변형 버전들이 제안되어 왔는데요. Rudolph는 teacher network의 구조를 invertible neural network로 제한시켜서 PatchCore에 버금가는 이상 탐지 성능에 도달하는 데 성공하기도 하였습니다. 본 논문에서는 Asymmetric Student Teacher (AST)  모델과 original S-T method, 그리고 EfficientAD를 비교합니다.

autoencoder나 GAN과 같은 생성 모델 또한 이상 탐지를 위해서 범용적으로 사용되어 왔습니다. 최근 autoencoder 기반의 방법들은 정상 이미지에 대해서는 정확한 복원을, 비정상 이미지에 대해서는 부정확한 복원을 한다는 것에 의존하고 있습니다. 이는 input image에 대한 복원 결과와 비교해서 이상 이미지를 찾아낼 수 있게 만들어줍니다.

이러한 접근법에서 발생하는 흔한 문제는 정상 이미지에 대한 부정확한 복원으로 인해 발생하는 false-positive detection 문제입니다. (정상인데 비정상으로 탐지되는 것이라고 이해하시면 됩니다.) 이를 피하고자, Bergmann은 autoencoder가 pretrained network의 feature space에서 이미지를 복원하도록 하였습니다. 게다가 해당 논문에서는 autoencoder의 output을 예측하는 neural network를 학습시켰는데, 이 network는 normal image에 대한 systematic reconstruction error도 학습하게 됩니다. (논문에서 이 systematic reconstruction error에 대한 설명이 막 자세하진 않은데, 제가 이해하기로는 autoencoder의 output에서 나타나는 global한/거시적인 경향성을 의미하는 것 같습니다. autoencoder의 복원 결과가 전반적으로 흐릿하다면, 이것의 output을 예측하도록 학습된 모델 또한 전반적으로 흐릿한 결과를 뽑게 된다는 것입니다.)

4. Method

저자들은 다음 subsection들에서 EfficientAD의 각 요소들을 설명하고 있습니다. 4.1에서는 pretrained neural network로부터 나오는 feature를 어떻게 효율적으로 추출할 것인지를 다룹니다. 4.2에서는 test time에서 student-teacher model을 사용해서 어떻게 anomalous feature를 검출하는지에 대해서 다룹니다. 주된 난관은 전체적인 runtime을 낮게 가져가면서도 경쟁력 있는 이상 탐지 성능을 가지는 것이었는데요. 이를 위해 student-teacher network를 학습하기 위한 loss function을 도입하였습니다. 이는 inference 시 연산량에 영향을 주지 않으면서 이상 탐지의 성능을 향상하게 됩니다.

4.3에서는 autoencoder 기반의 접근법을 사용해서 어떻게 logical anomaly를 잡는지를 설명합니다. 4.4에서는 student-teacher model과 autoencoder의 탐지 결과를 어떻게 결합하고 보정하는지에 대해서 설명하게 됩니다.

4.1 Efficient Patch Descriptors

최근 이상 탐지 방법들은 보통 WideResNet-101와 같은 pretrained network를 사용하는데요. 저자들은 깊이가 극단적으로 줄여진 네트워크를 feature extractor로 사용합니다. 이는 단 4개의 conv layer로 구성됩니다. 구조는 아래 Figure 2를 참고하시면 됩니다.

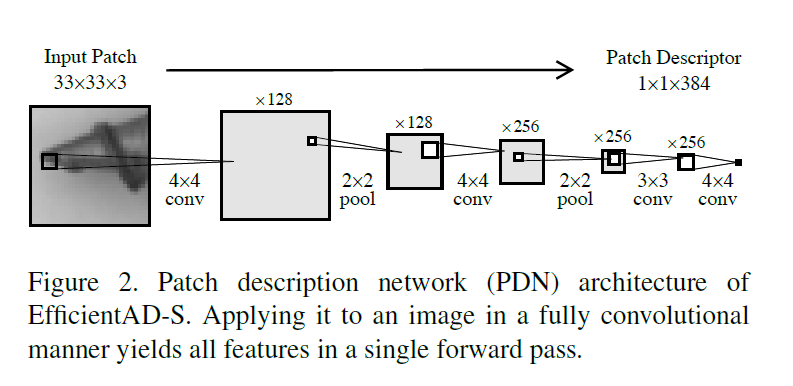
각 output 뉴런은 33x33 pixel의 receptive field를 가지고 있기 때문에, output feature vector의 각 요소들은 33x33 patch를 설명하게 됩니다. 이렇게 명확하게 대응되기 때문에, 저자들은 이 네트워크를 patch description network (PDN)이라고 명명했습니다. PDN는 한 번의 forward pass에 가변적인 사이즈의 이미지에서도 feature vector를 뽑아낼 수 있습니다.

'Uninformed Students: Student-Teacher Anomaly Detection With Discriminative Latent Embeddings' 논문에서도 유사하게 몇 개의 conv layer로만 이루어진 네트워크를 사용해서 feature를 뽑았는데요. 이러한 네트워크는 downsampling과 pooling이 없다 보니 꽤 높은 연산량을 요구했습니다. 

해당 논문에서 사용된 네트워크의 파라미터 수가 1.6 million에서 2.7 million 정도로 비교적 낮았지만, GCAD에서 사용했던 31 million 파라미터를 가진 U-Net보다도 시간도 오래 걸리고 메모리도 더 요구하는 것을 실험적으로 확인했습니다. 이는 파라미터의 수가 특정 방법론의 latency, throughput, memory footprint에 대한 적절치 못한 metric이라는 것을 의미한다고 합니다. 

최근 classification architecture들은 대부분 downsampling을 초기에 적용해서 feature map 사이즈를 줄이고, 시간 및 공간 복잡도를 감소시키는 편입니다. 저자들도 유사한 방식을 PDN에 적용, NVIDIA RTX A6000 GPU 기준 256x256 사이즈 이미지에서 feature를 얻는데 800μs가 소요된다고 합니다. (800μs = 0.8ms라고 보시면 됩니다.)

PDN이 expressive feature를 만들게 하기 위해서, 저자들은 deep pretrained classification network를 활용해 knowledge distillation를 적용합니다. ImageNet에 있는 이미지에 대해서 pretrained network에서 뽑은 feature와 PDN의 output 간의 MSE가 최소화되도록 학습이 진행됩니다. 

PDN은 매우 효율적인 것 외에도, 일반 deep network를 사용하는 것과 비교했을 때 또 다른 이점이 있는데요. PDN에서 만들어진 feature vector는 각 픽셀에 대응되는 33x33 patch에만 의존한다는 것입니다. 반면에, pretrained classifier에서 나온 feature는 이미지의 다른 부분에도 long-range dependency를 가지게 되죠. 이는 Figure 3을 보면 확인할 수 있습니다.

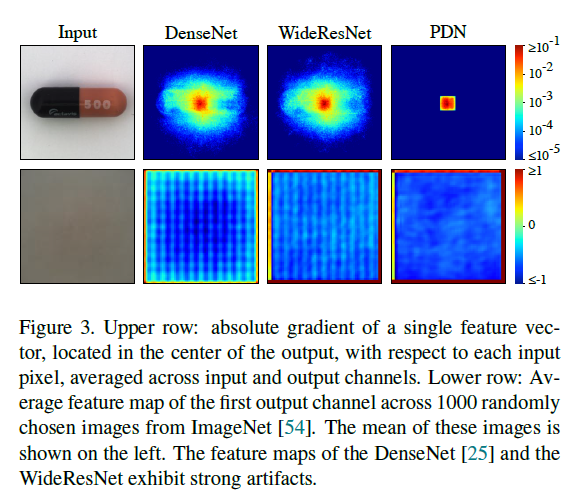
Figure 3의 위쪽 행은 output의 중심부에 위치한 1개의 feature vector에 대해서 각 input pixel에 대한 gradient를 나타낸 것입니다. 예를 들어서 모델의 output이 28x28이라고 하면, 아마 (14, 14)에 위치한 feature vector를 얘기하는 것 같은데요. 해당 vector 값에 대한 각 input pixel의 gradient 값을 시각화한 것으로 보입니다. 

DenseNet이나 WideResNet을 보시면, 해당 feature vector에 대한 gradient가 input image의 정중앙 pixel 외에도 꽤나 넓은 범위에 걸쳐서 분포해 있는 것을 알 수 있습니다. 위에서 언급된 대로, 이미지의 다른 부분에도 dependency가 있다는 게 바로 이런 의미입니다. 반면에, PDN은 매우 국소 부위만 영향을 미치는 것을 알 수 있으며, 이미지의 나머지 부위들은 gradient가 아주 작은 값인 것으로 보입니다.

이렇게 PDN은 well-defined receptive field를 가지고 있기 때문에, 이미지의 다른 부분들로 인해서 anomaly localization에 악영향을 주는 경우가 없을 것이라고 밝히고 있습니다.

4.2 Reduced Student-Teacher

anomalous feature vector를 탐지하기 위해서 teacher network로는 distilled PDN을 사용하고, 동일한 architecture를 student에도 그대로 적용합니다. 이를 통해서 1ms 이내로 feature를 뽑을 수 있게 됩니다.

그런데, 최근 모델들이 anomaly detection performance를 증가시키고자 사용한 방법들, 예를 들어 여러 개의 teacher network와 student network를 앙상블 한다던가, student와 teacher 간의 architectural asymmetry를 활용한다거나 하는 테크닉이 적용되지 않았습니다. 따라서, 저자들은 연산량에 영향을 주지 않으면서도 성능을 높이는 training loss를 도입했습니다.

저자들은 일반적인 S-T framework에서 학습 이미지의 수를 증가시키면 이상 이미지에 대해서 teacher network를 모방하는 능력이 향상되는 것을 확인했다고 합니다. 이는 이상 탐지 성능을 악화시키죠. 그렇다고 해서 학습 이미지 수를 너무 많이 줄이면 정상 이미지에 대한 중요한 정보를 얻지 못하게 될 수 있죠. 그래서 저자들은 student network에 충분한 이미지를 제공해서 정상 이미지에 대해서는 teacher network를 잘 모방하도록 만들면서, 동시에 anomalous image에 대해서 generalization 하지 못하도록 만들어보고자 했다고 합니다.

Online Hard Example Mining과 유사하게, 저자들은 student network가 teacher network를 가장 잘 못 따라 하는 부분만 loss에 영향을 주도록 했습니다. 즉, 가장 높은 loss값을 가진 output element만을 loss에 활용한다는 것입니다.

이를 수식으로 표현하자면, teacher network $T$와 student network $S$가 있고 training image $I$가 있으면, 각각은 $T(I) \in R^{C \times W \times H}$, $S(I) \in R^{C \times W \times H}$를 만들어 내게 됩니다. 각 $(c, w, h)$에 대해서 squared difference는 $D_{c, w, h} = (T(I)_{c, w, h} - S(I)_{c, w, h})^2$로 계산됩니다. 

mining factor $p_{hard} \in [0, 1]$을 기반으로, $D$에서 $p_{hard}$ quantile을 계산합니다. 이를 $d_{hard}$로 표현하고요. 위에서 구한 $D_{c, w, h}$에서 $d_{hard}$보다 크거나 같은 요소들의 평균을 training loss인 $L_{hard}$로 사용하게 됩니다. 

$p_{hard}$의 의미를 생각해 보면, 이를 0으로 했을 땐 일반적인 S-T loss라고 이해할 수 있죠. 실제로 저자들의 실험에서는, 이 값을 0.999로 지정했다고 합니다. 99.9 분위수라고 하니, 매우 높은 값 일부만 사용한 것을 알 수 있습니다. 이 $p_{hard}$의 효과는 Figure 4에서 볼 수 있습니다. 

hard feature loss를 사용하는 효과를 위 사진에서 볼 수 있는데요. 밝기는 backprop을 위해 사용된 feature vector의 차원이 얼마나 사용되었는지를 나타내고 있습니다. 못과 관련이 없는 background에는 하얀 요소들이 없는 것을 확인할 수 있으며, 이는 backprop에 사용되는 요소들이 없다는 것을 의미하고, stduent network의 output과 teacher network의 output 간의 difference가 적다는 것을 확인할 수 있습니다. 그래서 우리가 학습해야 할 사물 쪽 요소만 학습을 진행하게 됩니다.

Inference를 진행할 때 2D anomaly map $M \in R^{W \times H}$은 $M_{w, h} = C^{-1}\Sigma_{c}D_{c, w, h}$로 계산되며, 이는 채널 기반으로 평균을 낸 것이라고 이해하시면 되겠습니다. (표기상 $C^{-1}$로 표기 되어 마치 matrix처럼 보일 수 있지만, 실제로 $C$는 차원의 수 이기 때문에 512와 같은 int입니다. 그래서 실제로는 1/512와 같이 int 값의 역수라고 이해하시면 됩니다.) 

추가적으로, hard feature loss를 적용하면 normal image에 대해서 false-positive detection이 발생하는 경우를 피할 수 있는 장점도 있습니다. (정상이 anomaly로 탐지되는 것을 의미합니다.)

hard feature loss 외에도, 저자들은 loss penalty라는 것을 추가로 적용했는데요. 이는 학습 중에 student가 normal training image에 없는 이미지에 대해서 teacher를 따라 하는 것을 방해하기 위해 적용한다고 합니다. 제가 생각하기에는 조금 독특하다고 느꼈는데, student network의 학습 도중에 teacher network의 pretraining때 사용된 이미지를 학습에 사용합니다. 즉 ImageNet에 있는 이미지 중에 랜덤 하게 뽑아서 이를 학습에 활용한다는 것이지요.

이를 반영한 loss를 계산하면, $L_{ST} = L_{hard} + (CWH)^{-1}\Sigma_{c} \parallel S(P)_{c}\parallel^{2}_{F}$로 계산이 됩니다. 이 penalty는 out-of-distribution image에 대해서 student network가 teacher network를 모방하지 못하게 막는 역할을 합니다. 수식이 조금 어려워 보일 순 있지만, ImageNet에서 뽑은 임의의 이미지가 $P$이고, student network가 $S$이니, $S(P)$는 이미지를 넣어서 나온 output이라고 보시면 됩니다. 이를 제곱을 해주고 channel 기준으로 sum한 다음, $CWH$로 나눠줍니다. 앞에서도 언급드렸지만, $CWH$는 matrix가 아니고 int입니다.

4.3 Logical Anomaly Detection

anomaly 중에서 logical anomaly가 발생할 가능성을 배제할 수는 없는데요. logical anomaly는 물체가 잘못 위치해 있다거나 하는 경우를 얘기합니다. 그래서 이런 경우들까지 탐지할 수 있어야 합니다. 'Beyond Dents and Scratches: Logical Constraintsin Unsupervised Anomaly Detection and Localization.' 논문에서 제안된 것처럼, 저자들은 이를 잡아내기 위한 용도로 autoencoder를 사용합니다. Figure 5에 EfficientAD의 전체 방법론을 나타내주고 있습니다.

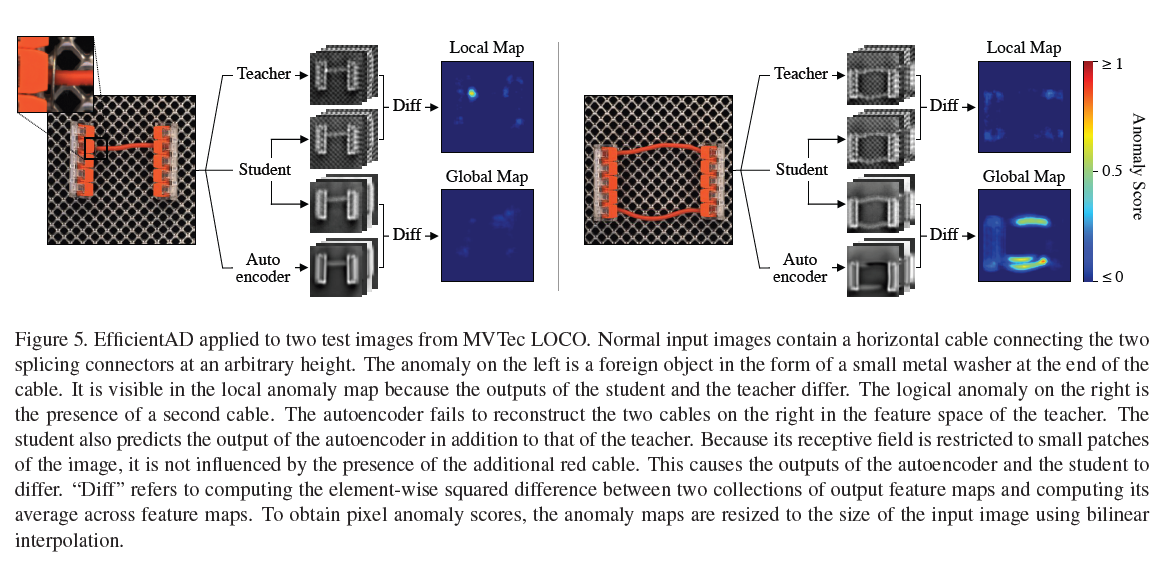
Figure 5를 확인해 보면, 앞에서 언급했던 student-teacher pair가 있고, 방금 전에 얘기한 autoencoder를 활용하는 것을 볼 수 있죠. autoencoder는 teacher network의 output을 예측하도록 학습된다고 합니다. 이를 수식으로 표현하자면, 이렇게 표현할 수 있습니다. Autoencoder는 $A$, training image $I$, 이를 활용하면 $A(I) \in R^{C \times W \times H}$를 output으로 뽑게 되죠. 그리고 autoencoder를 학습하는 데 사용할 loss는 $L_{AE} = (CWH)^{-1}\Sigma_{c}\parallel T(I)_{c} - A(I)_{c} \parallel^2_{F}$로 계산할 수 있습니다. $T$는 teacher network라고 하였으니, teacher network의 output과 autoencoder의 output 간 차이를 제곱해서 이를 평균 낸 값이라고 볼 수 있죠. 일반적인 autoencoder 학습에 사용하는 loss와 동일합니다.

student는 PDN이라는 것을 앞에서 언급했었는데요. student는 patch 기반의 network지만, autoencoder는 이미지 전체를 encode 하고 decode 하고 있습니다. 그래서 logical anomaly가 발생한 이미지에 대해서는 autoencoder가 복원을 제대로 못합니다. 하지만, 이러한 문제가 정상 이미지에도 발생하는데요. 이는 autoencoder가 fine-grained pattern 복원을 어려워하기 때문입니다. 이는 Figure 5에서도 확인할 수 있죠.

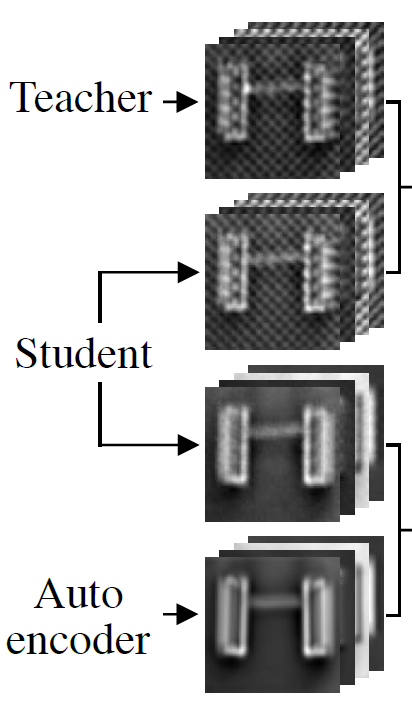
앞에서 언급했듯이, autoencoder는 teacher network의 output을 유사하게 따라가도록 학습되어 있는데요. 보시면 autoencoder에서 나온 output은 background에 있는 패턴들은 복원이 안된 걸 볼 수 있습니다. 이 부분을 얘기한다고 이해하시면 됩니다.

이런 문제 때문에 teacher network의 output과 autoencoder의 output 간 차이를 그대로 anomaly map으로 활용하기에는 false-positive가 발생할 수 있다고 합니다. 따라서, 저자들은 student network의 output channel의 수를 두배로 늘리고, 이를 autoencoder의 output과 teacher network의 output를 예측하도록 학습하도록 한다고 합니다.

이를 수식으로 표현하자면, $S'(I) \in R^{C \times W \times H}$가 student의 추가적인 output channel이라고 했을 때, student의 추가적인 loss는 다음과 같이 정의됩니다. $L_{STAE} = (CWH)^{-1}\Sigma_{c}\parallel A(I)_{c}-S'(I)_{c}\parallel^{2}_{F}$. 결론적으로 전체 training loss는 $L_{AE}$, $L_{ST}$, $L_{STAE}$의 합이라고 합니다.

이렇게 학습하면 student network는 autoencoder의 정상 이미지에 대한 systematic reconstruction error(예를 들면, 전체적으로 blurry 하게 복원되는 것)은 학습하면서, 동시에 anomaly에 대해서 발생하는 reconstruction error는 학습을 못하게 됩니다. 따라서, autoencoder의 output과 student network의 output 간 차이는 anomaly map으로 활용할 수 있게 됩니다. 이는 global anomaly map으로 부르게 되고요.

student network의 output과 teacher network의 output간 square difference를 계산하고, 이를 channel 기준으로 평균을 내서 이를 local anomaly map으로 활용합니다. 이 두 anomaly map을 결합해서 활용하고, maximum value를 image-level anomaly score로 활용합니다.

4.4 Anomaly Map Normalization

local과 global anomaly map이 있기 때문에, 이 둘을 통합해서 사용하기 전에 유사한 scale로 변경이 필요합니다. 이는 Figure 5에 나타난 것처럼, 양쪽 anomaly map 중에서 한쪽에서만 anomaly가 검출되었을 경우 중요하게 된다고 합니다. 그 외에도, 한 map에서의 noise가 결합된 map에서 정확하게 탐지하는 것이 어렵게 만들 수 있습니다.

정상 이미지에서의 noise의 scale을 추정하기 위해서 validation image를 별도로 사용한다고 합니다. 이들은 학습 셋에는 없는 이미지고요. 두 가지 anomaly map 각각에 대해서, validation image 전체에 대해서 모든 pixel anomaly score를 계산합니다. 그러고 나서 각각 계산된 pixel anomaly score(local, global)에 대해서 두 개의 $p$ qunatiles를 계산하는데, $q_{a}$는 anomaly score 0에 맵핑되고, $q_{b}$는 0.1에 맵핑되는 값입니다. test time에는, 계산된 각각의 맵핑에 맞춰서 normalized 된다고 보시면 됩니다. 뒤에 experiment 부분에서 보면, $q_{a}$는 0.9 quantile, $q_{b}$는 0.995 quantile을 선택해서 사용하는 것을 알 수 있습니다.

5. Experiments

실험 부분은 아주 간단하게만 정리하고 넘어가려고 합니다. 크게 EfficientAD-S와 EfficientAD-M이 있다는 점만 알아두시면 되고, EfficientAD-M은 conv layer의 커널 수를 두배로 늘린 것입니다. 뒤에 보시면 S와 M 각각 레이어 구성에 대해서도 다 자세히 나와 있습니다. 실험은 MVTec AD, VisA, MVTec LOCO 데이터셋에서 진행하였고요.

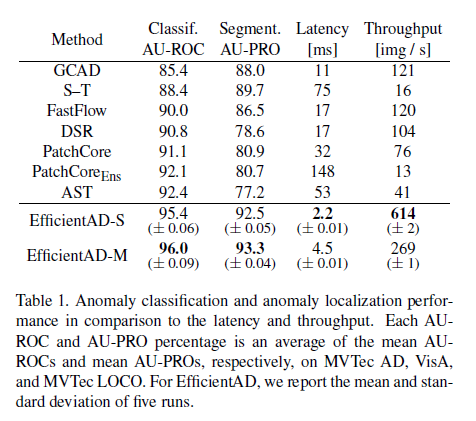
Table 1은 3개의 데이터 셋 전체에 대해서 평균 성능을 보여주고 있고, 나머지 방법론에 비해서 EfficientAD가 좋은 성능을 낸다는 점을 확인할 수 있습니다. 

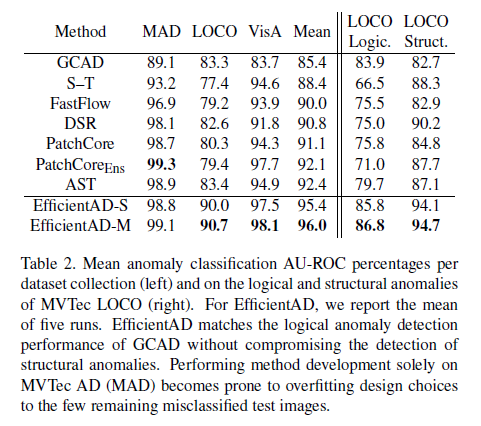
Table 1에 대한 세부적인 내용이 Table 2에 적혀있네요. MVTec AD에 대해서는 PatchCore, PatchCore ensemble, AST 모두 98 후반대가 나오고 있어서 이미 성능 기준으로는 saturation 된 상황인데, MVTec AD LOCO 데이터셋에 대해서 성능 차이가 심합니다. 아마 LOCO는 logical anomaly가 많아서, 기존 방법론으로는 탐지가 어려운 것이 아닐까 생각됩니다. 그래서 3개 데이터 셋에 대한 평균을 내니까 EfficientAD가 SOTA로 찍히는 모습입니다.

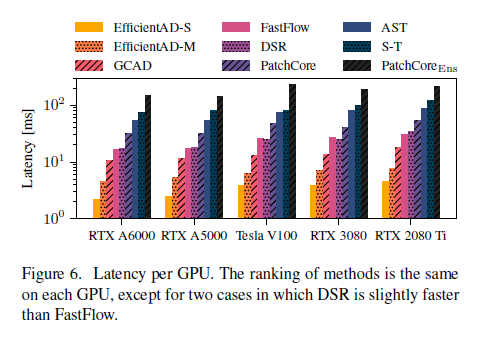
여러 가지 GPU에 대해서 Latency를 비교한 표입니다. EfficientAD가 가장 낮은 수준을 나타내고 있습니다. 

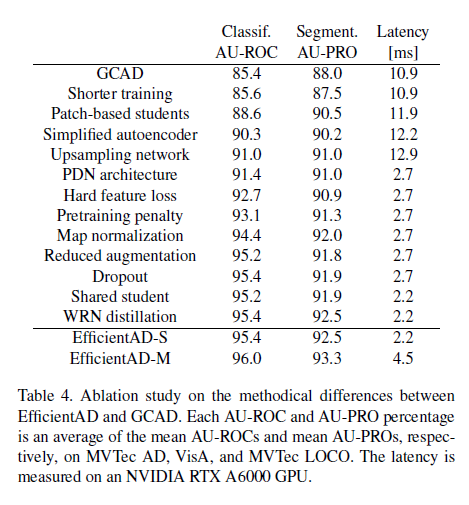
Table 4는 GCAD라는 모델에서 Ablation study를 진행한 모습입니다. 각각의 요소를 반영할 때마다 성능의 변화와, Latency의 변화를 보여주고 있습니다. 이 부분을 제대로 이해하려면 GCAD라는 모델에 대해서도 자세히 알면 더욱 이해하기가 쉽겠네요. 저는 아직 읽어본 논문이 아니라서 대략 감만 잡는 정도로 읽고 넘어갔습니다.

6. Conclusion

강력한 이상 탐지 성능과 매우 높은 연산 효율성으로 무장한 EfficientAD를 소개하는 논문이었습니다. 이는 logical anomaly와 structural anomaly를 모두 탐지하는 새로운 표준이 될 것으로 보이고요. 

강력한 이상 탐지 성능과 높은 연산 효율성을 기반으로 하면 이를 실제 application 환경에서 적용하기에 좋을 것으로 보이네요. 추가로 논문에서 제안한 PDN를 활용하면, 다른 이상 탐지 방법론에서도 latency를 줄이는데 도움이 될 것이라고 합니다.

7. Limitations

Student-teacher model과 autoencoder는 각각 다른 유형의 anomaly를 탐지하도록 설계가 되어 있는데요. Autoencoder는 logical anomaly를, student-teacher network는 fine-grained structural anomaly를 탐지하는 역할입니다. 하지만, fine-grained logical anomaly는 여전히 도전적인 문제로 남아 있는데요. 예를 들면 2mm만큼 더 긴 나사 같은 게 있겠죠. 이런 것들을 잡아내려면, 전통적인 측량 방법론들을 사용해야 한다고 합니다.

최근 이상 탐지 방법론들과 비교했을 때 한계점으로는, kNN 기반 방법론들과는 대조적으로 autoencoder를 별도로 학습해야 합니다. 

여기까지 해서 EfficientAD 논문을 정리해 보았습니다.

기존 방법론들이 단순히 pretrained CNN model에서 feature extraction을 하던 것에서 knowledge distillation을 통해 더 단순한 모델을 활용해서 feature extraction이 가능하도록 만들었다는 점이 굉장히 인상적이었고요.

또 일반적인 결함 외에도 logical anomaly까지 잡아내기 위해서 autoencoder까지 end-to-end로 연결한 process를 만들었다는 점도 흥미로웠던 것 같습니다.

논문 내용을 어느 정도 이해하셨다면, 논문 뒤에 있는 Appendix A을 확인해 보시면 전체 프로세스를 pseudo-code 형식으로 정리한 내용이 있습니다. 논문에서 언급된 요소들이 실제 어떤 흐름으로 진행되는지를 확인하실 수 있습니다.

추후 또 흥미로운 이상 탐지 논문을 발견하게 되면 리뷰를 진행해 보겠습니다.

감사합니다.

안녕하세요. 오랜만에 블로그 포스팅 올려보네요.

일하다가 torch.cdist라는 함수와 마주치게 되었는데, 마침 구글링을 해보니 한국어 자료가 0개여서 누군가에게 도움이 되고자 이렇게 포스팅을 만들게 되었습니다.

그럼 시작해보도록 하겠습니다.

torch.cdist의 공식 document의 주소는 다음과 같습니다.

https://pytorch.org/docs/stable/generated/torch.cdist.html

해당 함수에 대해서 설명하는 내용을 읽어보면, 'Computes batched the p-norm distance between each pair of the two collections of row vectors'라고 적혀 있습니다.

쉽게 말씀드리자면, 두 개의 벡터에서 각 행의 pair끼리의 p-norm distance를 구한 것이라는 설명입니다.

물론 이렇게 말씀드리면 이해하기가 어려우실 수 있으니, 이번에도 예시를 통해서 설명드리도록 하겠습니다.

p-norm에 대한 설명은 다른 블로그들이나 자료들을 참고해서 이해해주시고 본 포스팅에서는 별도로 설명드리지 않습니다.

import torch
import numpy as np

먼저 예시를 만들기 위한 library 두개를 import 해줍니다. pytorch와 numpy가 필요합니다.

a = torch.tensor(np.arange(1, 7).reshape(1, 3, 2), dtype=torch.float64)
print(a)

b = torch.tensor(np.arange(0.1, 0.9, 0.1).reshape(1, 4, 2))
print(b)

예시를 위해서 1부터 6까지 구성되는 numpy array를 만들고, (1, 3, 2)로 reshape 한 뒤에 torch tensor로 변환합니다.

또, 0.1부터 0.8까지 구성되는 numpy array를 만들고, (1, 4, 2)로 reshape 한 뒤에 torch tensor로 변환합니다.

참고로 torch.cdist는 column의 size가 동일한 vector끼리만 연산이 가능합니다. 따라서, 두 vector는 2차원으로 만들어두었습니다.

위 코드를 실행하면 다음과 같은 결과를 얻을 수 있습니다.

print(torch.cdist(a, b))

앞에서 선언한 a와 b를 torch.cdist를 이용해서 연산해줍니다.

이를 이용하면 다음과 같은 결과를 볼 수 있습니다.

값들이 꽤나 복잡하죠? 이에 대한 설명을 드리도록 하겠습니다.

앞에서 정의했던 a와 b는 다음과 같은 vector입니다. shape는 각각 Bx3x2와 Bx4x2로 정의하였습니다. B는 Batch size이며, 현재 예시에서는 1로 적용하였습니다. 

torch.cdist에서는 a 벡터의 row와 b 벡터의 row를 각각 pair로 만들고, 이에 대한 distance를 계산하게 됩니다.

a 벡터의 첫 번째 row와 b 벡터의 첫 번째 row, a 벡터의 첫 번째 row와 b 벡터의 두 번째 row.... 이런식으로 해서 a 벡터의 세 번째 row와 b 벡터의 네 번째 row까지 모두 pair를 만들면 총 몇 개의 pair가 만들어질까요?

3x4=12개의 pair가 만들어집니다.

그래서 위에서 보여드린 document에서는 다음과 같은 내용을 담고 있습니다.

만약 x1이 P 개의 row를 가지고 있고, x2가 R 개의 row를 가지고 있으면, 총 P x R 개의 pair가 만들어지므로, 결과값의 shape가 P x R 이라는 얘기입니다.

다시 위 예시로 돌아가서, 직접 한 개씩 연산을 진행해보겠습니다.

먼저 a 벡터의 첫 번째 row와 b 벡터의 첫 번째 row를 pair로 만들고, 이 둘 간의 distance를 계산해줍니다.

이를 output 벡터의 (1, 1) 위치에 적어줍니다.

다음으로는 a 벡터의 첫 번째 row와 b 벡터의 두 번째 row를 pair로 만들고, 이 둘 간의 distance를 계산해줍니다.

이를 output 벡터의 (1, 2) 위치에 적어줍니다.

이러한 방식으로 진행하기 때문에, output 벡터의 column 개수는 b 벡터의 row와 같아지게 됩니다. 

왜냐하면 b 벡터의 row 개수 만큼 계산을 진행해서, 이를 가로로 펴는 방식이기 때문이지요.

다음으로 a 벡터의 두 번째 row와 pair를 지어볼까요?

아무래도 수식이 커지다보니 그림이 작아졌네요.

a 벡터의 두 번째 row와 b 벡터의 첫 번째 row가 pair가 되어, 계산 결과가 output의 (2, 1) 위치에 오게 됩니다.

즉, 이러한 방식으로 진행되므로 output 벡터의 row 개수는 a 벡터의 row 개수가 같아지게 됩니다.

앞에서 설명한 방식을 전부 실행하면 다음과 같은 결과를 볼 수 있습니다.

이번 포스팅에서는 간단하게 torch.cdist 함수가 어떻게 작동하는지 예시를 통해서 준비해보았습니다.

감사합니다.

cv2.error:OpenCV(3.4.2) /tmp/build/80754af9/opencv-suite_1535558553474/work/modules/core/src/arithm.cpp:223:error:(-209:sizes of input arguments do not match) The operation is neither 'array op array' (where arrays have the same size and type), nor 'array op scalar' nor 'scalar op array' in function 'binary_op'

Python의 OpenCV(cv2)에서 cv2.bitwise_and()를 사용할 때 발생했던 에러입니다.

해당 오류가 발생하는 이유는 굉장히 다양해서, 해당 에러에 대한 해결방안을 적은 블로그 글에서 조차 다양한 해결방안을 제시하고 있습니다.

해당 에러에서의 핵심은 'where arrays have the same size and type'이라고 보여지며, 말 그대로 opencv 연산을 하고자 하는 array의 size와 type이 같아야 한다는 점입니다.

제 케이스에서는 size가 같았으나 에러가 나서, 변수의 .dtype을 찍어보니 하나는 float32였고, 다른 하나는 float64이였습니다.

이에 대응하고자 float64인 이미지를 .astype(np.float32)로 처리하여 float32로 맞춰주었더니 해결되었습니다.

안녕하세요.

오늘은 scipy.ndimage.label과 skimage.measure.regionprops를 이용해서 이미지 내에서 threshold 이상의 값을 가지는 위치를 찾는 작업을 해보려고 합니다.

구글링 해보니 한국어로 된 자료가 검색이 잘 안되어서, 작성해두면 많은 분들께 도움이 되지 않을까 싶어 작성하게 되었습니다.

예시 코드들을 첨부해보면서, 하나하나 같이 익혀보겠습니다.

그럼 시작해보겠습니다.

이미지 내에서 특정 값 이상을 가지는 위치를 어떻게 하면 찾을 수 있을까?

먼저, 필요한 library를 import 해줍니다.

import numpy as np
import scipy
from scipy.ndimage import label
from skimage.measure import regionprops

저는 이해를 돕기 위해, 임의로 numpy array를 생성하여 설명을 드리겠습니다.

원리만 이해한다면, 일반적으로는 제가 설명드리는 예시보다 훨씬 더 큰 이미지 내에서도 동일한 작업을 수행하실 수 있을 겁니다.

(혹시나 pytorch나 tensor flow 등 deep learning framework를 사용하신다면, 대부분 .numpy()를 통해 tensor 형태의 데이터를 numpy array로 전환하실 수 있습니다.)

이해를 돕기 위해, 간단하게 (6, 6) 짜리 numpy array를 생성해줍니다.

image = np.array([[1, 2, 3, 4, 4, 4],
               [1, 2, 6, 10, 9, 7],
                [2, 3, 11, 15, 16, 7],
               [1, 2, 7, 8, 9, 7],
               [6, 7, 8, 9, 10, 7],
               [4, 4, 4, 4, 4, 4]])

아까 import 했던 scipy.ndimage.label을 사용할 시간입니다.

제가 하고 싶은 작업은, 해당 image에서 6보다 큰 부위를 찾아내고 싶습니다.

따라서, 다음과 같은 코드를 작성해줍니다.

labeled, nr_objects = label(image > 6)
print(labeled)

여기서 labeled는 입력으로 준 image 중에서 6보다 큰 지점들에 label을 주게 됩니다.

print를 해보면 다음과 같이 나오게 됩니다.

이렇게 하게 되면, labeled 된 지점들만 추출해 위치를 잡을 수 있게 됩니다.

그리고 nr_objects의 경우는 1이 됩니다.

이걸 보시고 이런 생각을 하실 수 있을 것 같습니다.

만약 특정값보다 큰 지점들이 저렇게 다 연결되어 있는 것이 아니라, 조금씩 조금씩 모여있는 경우는 어떻게 될까?

그런 경우도 보여드리겠습니다.

먼저, 기존에 사용했던 image의 값을 다음과 같이 변경해줍니다.

image = np.array([[1, 2, 3, 7, 7, 7],
               [1, 2, 6, 10, 9, 7],
                [2, 3, 4, 4, 4, 4],
               [1, 2, 7, 8, 9, 7],
               [6, 7, 8, 9, 10, 7],
               [4, 4, 4, 4, 4, 4]])

이렇게 설정하고 나서, 다시 label을 찍어보면 다음과 같이 되는 것을 보실 수 있습니다.

이번에는 오른쪽 상단에 한 구역과 오른쪽 하단에 한 구역으로, 총 두 구역이 잡히게 됩니다.

이처럼, 특정 값보다 높은 지역이 모두 연결되는 것이 아니라 분리되어 있을 경우, label이 1, 2,... 등으로 매겨지면서 지점을 찾아주게 됩니다.

그리고 이렇게 두 구역이 잡히는 경우, nr_objects는 2가 됩니다. 

즉, nr_objects는 구역의 개수를 뜻한다는 것이죠.

자 그럼, 여기까지 진행하면 내가 가지고 있는 이미지에 대해서 특정 값보다 높은 값을 가지는 구역에 대해 labeling 작업이 된 것이죠?

다음으로는 그 구간의 좌표와 면적을 구해보겠습니다.

아까 구해둔 labeled라는 변수를 이용해서 skimage.measure.regionprops를 이용합니다.

# regionprops : Measure properties of labeled image regions.
props = regionprops(labeled)

props라는 변수로 regionprops 객체를 저장하였는데요. 

이는 다음과 같은 것을 포함합니다.

RegionProperties의 list이죠. 따라서 이는 type을 찍어보면 list가 됩니다.

다음으로는 이 RegionProperties의 property를 사용해서 여러 가지 정보를 얻어보겠습니다.

먼저, 구역이 1개인 기존 케이스에 대해서 적용해보겠습니다.

props가 list이므로, list 내부에 있는 값들에 대해서 적용하기 위해 for문을 적용해줍니다.

b.area는 labeled 된 구역의 pixel 개수를 구해줍니다. 

이전 사진에서 확인하실 수 있겠지만, 1로 labeled 된 pixel은 총 16개입니다.

b.bbox_area는 bounding box의 pixel 개수를 구해줍니다.

bounding box는 labeled 된 구역을 감싸는 box를 생성하게 되는 것으로, b.area보다는 크거나 같은 값이 나오게 됩니다.

b.image는 bounding box와 같은 사이즈를 가지고 있는 binary region image를 보여줍니다.

따라서, False와 True로 표시된 저 값이 실제 bounding box의 크기와 동일하고, bounding box 내에서 labeled 된 데이터와 unlabeled 데이터가 어떻게 구성되어 있는지 확인할 수 있습니다.

b.bbox의 경우는 Bounding box의 정보를 출력해주게 되며, (min_row, min_col, max_row, max_col)의 형태로 출력을 내줍니다. 

주의해야 할 사항은, bounding box에 속하는 pixel은 half-open interval [min_row; max_row)와 [min_col; max_col)에 속하게 됩니다.

그렇다면, 이 b.bbox를 어떻게 해석해볼 수 있을지 알아봐야겠죠?

기본적으로 col은 가로, row는 세로를 뜻하는 것을 기억해주셔야 하고,

index는 0부터 시작합니다.

이전에 labeled 된 데이터를 보여드렸었는데, 이걸 가지고 설명을 드리겠습니다.

빨간색이 row, 파란색이 col입니다.

방금 bounding box는 half-open interval에 속한다는 말씀을 드렸었는데, 먼저 row부터 보겠습니다.

row는 [min_row; max_row) 범위에 속하게 되는데, 해당 image 데이터 기준으로 보자면 bounding box를 그린다고 했을 때 세로 기준으로 1부터 4까지 그려지는 게 맞겠죠? 

근데, max_row는 open입니다. 아마 고등학교 수학에서 open(열린 구간)과 close(닫힌 구간)의 개념을 배우셨겠지만, 쉽게 얘기하면 max_row에는 등호가 없습니다.

따라서, bounding box 기준에서 봤을 때는 min_row는 1이고, max_row는 5입니다.

쉽게 부등호로 표현하자면 1 <=row <5라는 것입니다.

col도 보겠습니다.

마찬가지로 col도 [min_col; max_col) 범위에 속하게 됩니다.

해당 image 데이터 기준으로 bounding box는 1부터 5까지 그려지는 게 맞겠죠?

그렇다면 bounding box 기준에서 봤을 때 min_col은 1이고, max_col은 6이게 됩니다. 

그래서, 아까 보여드렸던 이 그림에서 b.bbox의 값들이 이렇게 나온 것입니다.

(1, 1, 5, 6)인 것을 확인하실 수 있죠.

다음으로는 이 값들을 이용해서 bounding box의 xy starting point와 width, height를 계산해보겠습니다.

bounding box를 그리려면 starting point와 width, height가 필요한데, 먼저 b.bbox [1]이 x 좌표의 시작점이 됩니다.

그리고 b.bbox [0]이 y 좌표의 시작점이 되지요.

width는 가로를 의미하므로, max_col과 min_col을 뺀 b.bbox [3] - b.bbox [1]이 되고, 

height는 세로를 의미하므로, max_row와 min_row를 뺀 b.bbox [2] - b.bbox [0]이 됩니다.

이 정보를 이용해서 원하시는 곳에 bounding box를 그리시면 됩니다...!

아까 label 쪽을 설명하면서 특정값 이상인 구역이 여러 개인 경우에 대해서도 말씀을 드렸는데, for b in props: 코드를 진행하시게 되면 이렇게 여러 개인 경우 bounding box가 여러 개 나오게 됩니다.

이를 이용해서 여러 개의 bounding box를 그리시면 되겠습니다.

원리는 당연히 동일하므로, 이 부분에 대해서는 별도로 제가 예시를 들어 설명을 해드리지 않아도 될 것 같습니다.

여기까지 해서 scipy.ndimage.label과 skimage.measure.regionprops를 활용해 특정값보다 큰 값을 가지는 이미지의 위치를 잡아내는 방법을 소개해보았습니다.

분명 다양한 이미지 task에 사용할 수 있는 방법이라고 생각이 되고, 유용한 자료가 되었으면 좋겠습니다.

감사합니다.

안녕하세요. 오늘은 torch.nn.ConvTranspose2d 라고 하는 모듈에 대해서 알아보도록 하겠습니다.

용어로는 Deconvolution이나 fractionally-strided convolution이라고 불리는 작업을 수행합니다.

해당 작업이 무엇인지를 자세하게 다룬 자료들은 이미 너무 많이 있어 생략하고, 실제로 연산되는 결과를 위주로 살펴보겠습니다.

이 모듈은 Deep Convolutional GAN을 구현할 때 주로 사용됩니다.

그럼 시작해보겠습니다.

분석 코드

import torch
import torch.nn as nn

# sample values.
test_input = torch.Tensor([[[[1, 2, 3], [4, 5, 6]]]])
print("input size: ", test_input.shape)
print("test input: ", test_input)

먼저, pytorch를 이용해서 실험해 볼 것이기 때문에 모듈을 불러오고요.

input으로 들어갈 tensor를 만들어줍니다.

사이즈가 작으면서도 직관으로 이해해보기 쉽도록 다음과 같이 만들었습니다.

굳이 4차원으로 만드는 이유는, pytorch에서는 기본적으로 4차원 input만을 지원하기 때문입니다.

따라서, 실제로 값이 있는 것은 1부터 6까지로 해서 2 x 3 형태이지만, shape를 맞추기 위해 4차원으로 구성되었다고 보시면 될 것 같습니다.

# sample model. It has nn.ConvTranspose2d(1, 3, 4, 1, 0, bias = False)
# First parameter = Channels of input (=1)
# Second parameter = Channels of output (=3)
# Third parameter = Kernel size (=4)
# Fourth parameter = stride (=1)
# fifth parameter = padding (=0)
class sample(nn.Module):
  def __init__(self):
    super(sample, self).__init__()
    self.main = nn.ConvTranspose2d(1, 3, 4, 1, 0, bias = False)

  def forward(self, input):
    return self.main(input)

다음으로는 우리가 오늘 살펴보려고 하는 메인인 nn.ConvTranspose2d를 가지고 있는 모델을 하나 만들어줍니다.

위에 주석에 달려있듯이, 첫 번째 파라미터는 input의 채널수이고 두 번째 파라미터는 output의 채널 수이며

세 번째 파라미터는 kernel size, 네 번째 파라미터는 stride, 다섯 번째 파라미터는 padding입니다.

계산을 조금 더 간단하게 하기 위해 bias= False로 놓고 실험해보겠습니다.

별도의 신경망 연산이 필요 없으므로, 매우 간단하게 layer 딱 1개만 있는 모델을 만들었습니다.

Model = sample()

# Print model's original parameters.
for name, param in Model.state_dict().items():
  print("name: ", name)
  print("Param: ", param)
  print("Param shape: ", param.shape)

만들어진 모델의 기본 weight를 살펴보겠습니다.

pytorch가 기본적으로 지원하는 초기화 방법에 따라, weight 값이 결정된 것을 확인할 수 있습니다.

그리고 shape는 [1, 3, 4, 4]를 가지게 됩니다. 

이는 kernel size를 4로 지정했기 때문에, filter의 사이즈가 4x4 형태가 되어서 그렇고 output의 channel을 3으로 지정하였으므로 결괏값이 3개의 채널로 나와야 해서 3이 생겼다고 보시면 되겠습니다.

쉽게 해당 convolution 필터를 가로가 4, 세로가 3, 높이가 4인 직육면체로 생각하시면 편합니다.

그림으로 표현해보자면 다음과 같은 것이죠.

다음으로는 결과를 조금 더 쉽게 보기 위해서, model의 파라미터를 manually 하게 바꿔보겠습니다.

지금은 weight가 소수점으로 되어 있고 매우 복잡하기 때문에, 결과를 직관적으로 이해해볼 수 있기 위한 작업입니다.

# I makes 48 values from 0.1 to 4.8 and make (1, 3, 4, 4) shape
np_sam = np.linspace(0.1, 4.8, num = 48)
np_sam_torch = torch.Tensor(np_sam)
sam_tor = np_sam_torch.view(1, 3, 4, 4)


# Modify model's parameters using 4 for loops.
with torch.no_grad():
    batch, channel, width, height = Model.main.weight.shape
    
    for b in range(batch):
        for c in range(channel):
            for w in range(width):
                for h in range(height):
                    Model.main.weight[b][c][w][h] = sam_tor[b][c][w][h]

# Check parameter modification.
print("Model weight: ", Model.main.weight)

먼저, np_sam이라는 변수로 np.linspace를 이용해 0.1부터 4.8까지 48개의 값을 만들어줍니다. 이렇게 하면 0.1, 0.2, 0.3 .... 4.8까지 0.1을 간격으로 하는 숫자 48개를 만들 수 있습니다.

그리고 이를 torch.Tensor로 바꿔주고, shape를 맞추기 위해 (1, 3, 4, 4)의 형태로 맞춰줍니다.

다음으로는 model의 파라미터를 수동으로 바꿔주는 코드입니다.

먼저 batch, channel, width, height라는 변수로 model의 weight의 shape를 받습니다.

그리고 이를 4중 for문을 이용해서 바꿔줍니다.

Model.main.weight[b][c][w][h]의 값을 해당하는 인덱스와 동일한 sam_tor의 위치의 값으로 바꾸는 것이죠.

물론 일반적으로 computational cost 때문에 4중 for문을 사용하는 것은 비효율적이긴 하지만, 어쨌든 이번 상황에서는 각 차원별로 값이 작기 때문에 연산 자체가 오래 걸리진 않아 이렇게 코드를 짜보았습니다.

그리고 마지막으로는 model의 weight들을 print 해봅니다. 실제로 우리가 원하는 대로 잘 바뀌었는지 봐야겠죠.

역시나 원하는 대로 잘 바뀌었네요. 

이렇게 값들이 simple해야 우리가 결과를 찍었을 때 해석도 쉬울 것입니다.

이것도 아까와 마찬가지로 shape가 (1, 3, 4, 4)가 될 텐데요, 이 또한 직육면체 형태로 이해해 볼 수 있습니다.

모든 원소의 값이 다 보이시도록 최대한 길게 그렸는데요. 이처럼 가로가 4, 세로가 3, 높이가 4를 만족하는 직육면체를 생각하시면 됩니다.

result = Model(test_input)

print("Result shape: ", result.shape)
print("Result: ", result)

다음으로는, 아까 만들어뒀던 (1, 1, 2, 3) 짜리 input을 위에서 보여드린 weight을 이용해서 nn.ConvTranspose2d를 사용해 연산한 결과를 출력합니다.

결과가 어떻게 나오는지 보겠습니다.

뭔가 어떤 결과가 나왔는데, 이것만 봐서는 아직 어떤 식으로 연산이 이루어지는지 알 수 없겠죠?

그래서 제가 하나하나 한번 뜯어서 분석해보았습니다.

실제 구동 방법 분석

이해를 조금 쉽게 하기 위해서, 파라미터와 결과 모두 channel을 1차원으로 가정하고 살펴보겠습니다.

먼저, 우리의 input은 다음과 같은 2 x 3 형태의 tensor가 됩니다.

이를 우리가 설정한 parameter를 이용해서 단순히 곱해줍니다.

따라서 다음과 같은 결과를 볼 수 있습니다.

다음으로는 다른 input 요소들도 어떻게 계산되는지 보겠습니다.

자 그러면 input 1부터 6까지 연산을 완료했다면, 결과가 총 6개가 나오게 되겠죠?

나온 6개의 결과를 element-wise addition을 통해서 최종 결과를 뽑아냅니다.

이것이 아까 프로그램을 돌려서 나온 결과와 일치함을 확인할 수 있습니다.

따라서, nn.ConvTranspose2d의 연산 과정을 다음과 같이 정리해볼 수 있습니다.

1. nn.ConvTranspose2d를 만들 때 input값의 channel 수와 설정한 output channel 수, kernel size를 고려하여 weight를 만들어낸다.

우리의 경우에는 output channel을 3으로 지정하였고, kernel size를 4로 지정하였으므로 

weight의 크기가 (1, 3, 4, 4)가 됩니다. 

만약에 input의 channel 수가 3이고, output channel 수가 7이며 kernel size가 4였다면

weight의 크기가 (3, 7, 4, 4)가 될 것입니다.

즉, weight의 크기는 (input channel, output channel, kernel size, kernel size)가 됩니다.

2. input의 각 element 별로 weight와 곱해줍니다. 만약 stride가 1보다 크다면, 그 값만큼 이동하면서 만들어줍니다.

위에서의 예시는 stride 1인 경우를 봤었죠. input의 각 element 별로 weight와 곱해준 결과를 stride 1로 이동하면서 만들어냈습니다.

3. 나온 모든 결괏값을 element-wise 하게 더해서 최종 결과를 냅니다.

stride가 kernel size보다 작게 되면 서로 겹치는 부분들이 존재합니다. 그럴 때는 단순히 element-wise하게 더해서 결과를 내주면 됩니다.

마지막으로, batch size가 1보다 클 때의 결과도 한번 정리해보면서 마무리 짓겠습니다.

만약 input이 (4, 3, 4, 4)의 사이즈를 가지고 있고, 모델이 nn.ConvTranspose2d(3, 7, 4, 1, 0, biase = False)인 layer를 가지고 있다고 가정한다면 어떻게 될까요?

먼저 parameter의 값들부터 확인해보겠습니다.

input channel이 3이고, output channel이 7이며, kernel size는 4이고, stride는 1이며 padding은 0인 경우입니다.

그렇다면 weight는 shape가 어떻게 될까요?

위에서 얘기한 내용을 적용해보면, (3, 7, 4, 4)가 됨을 알 수 있습니다.

마지막으로 output의 결과는 어떻게 될까요?

batch size는 그대로 4가 될 것이고, output channel을 7로 정했으니 channel 수는 7이 되겠죠?

그리고 stride = 1인 상황이고 padding = 0이니까, input 각각에 대해서 kernel size 4 만큼 확장이 되므로

이것이 1칸씩 이동하는데 input 사이즈가 4개니까, 총 7이 됩니다. (input이 1개면 4, 2개면 5, 3개면 6, 4개면 7이 되는 것이죠. stride = 1이므로 하나씩 이동한다고 보시면 될 것 같아요.)

따라서 output의 결과는 (4, 7, 7, 7)이 됩니다.

지금까지 nn.ConvTranspose2d가 어떻게 작동하는지에 대해서 세세하게 알아봤습니다.

예시에서는 조금 더 와닿게 만들기 위해서 batch size가 1일 때를 가정하고 설명하였으나,

사실상 batch size는 input와 output에서 변동되는 요소가 아니므로 크게 신경 쓰지 않아도 되는 부분이라고 생각합니다.

혹시라도 보시면서 더 궁금하신 점이나 이해가 안 되시는 점이 있다면 댓글로 추가적으로 설명을 드릴 수 있을 것 같습니다.

이번 포스팅은 여기서 마치겠습니다.

앞에서 다룬 다항식 곡선 피팅 예시에서 가장 좋은 일반화 능력을 가지는 최적의 다항식 차수가 있다는 것을 확인할 수 있었습니다.

다항식의 차수에 따라서 모델의 자유 매개변수의 수가 결정되며, 이에 의해서 모델의 복잡도가 결정되게 됩니다.

또한, 정규화된 최소 제곱법의 경우에는 정규화 계수 $\lambda$도 모델의 실제적인 복잡도에 영향을 미쳤습니다.

혼합 분포나 신경망 등의 더 복잡한 모델의 경우 복잡도를 통제하는 매개변수가 더 많을 수도 있습니다.

실제 응용 사례에서는 이러한 매개변수들의 값을 결정해야하며, 이때의 목표는 새로운 데이터에 대한 예측 성능을 최적화하는 것입니다. 

주어진 한 모델의 매개변수의 값을 결정하는 것뿐만이 아니라 다양한 여러 모델들을 고려하여 해당 응용 사례에 가장 적합한 모델을 선택해야 할 경우도 있습니다.

최대 가능도 접근법에서 이미 확인한 것과 같이, 훈련 집합에서의 좋은 성능이 반드시 좋은 예측 성능을 보장해 주지는 못합니다. 이는 과적합 문제 때문입니다. 이를 해결할 한 가지 방법은 데이터가 충분할 경우 일부의 데이터만 사용하여 다양한 모델과 모델의 매개변수들을 훈련시키고 독립적인 데이터 집합인 검증 집합(Validation set)에서 이 모델들과 매개변수들을 비교 / 선택하는 것입니다.

만약 한정된 크기의 데이터 집합을 바탕으로 반복적으로 모델 디자인을 시행한다면, 검증 집합에 대해서도 과적합 문제가 발생할 수 있습니다. 이런 상황을 방지하기 위해 시험 집합(Test set)을 따로 분리해 두고 이 집합을 통해서 선택된 모델의 최종 성능을 판단하는 것이 좋을 수도 있습니다.

하지만 대부분의 실제 경우에는 데이터의 공급이 제한적이므로, 시험 집합을 별도로 분리해서 사용하는 것이 부담스러울 수 있습니다.

그리고 검증 집합의 크기가 작을 경우는 예측 성능에 대한 추정값이 정확하지 않을 수도 있습니다.

이러한 딜레마를 해결할 수 있는 한 가지 방법은 바로 교차 검증법(Cross validation)입니다.

그림 1.18은 교차 검증법을 설명하는 그림입니다. 

교차 검증법은 전체 데이터(S) 중 데이터의 (S-1) / S비율만큼 훈련에 사용하고, 모든 데이터를 다 활용하여 성능을 추정할 수 있습니다.

특히 데이터가 부족할 경우에는 S = N의 교차 검증법을 고려할 수도 있습니다. 여기서 N은 전체 데이터 포인트의 숫자입니다.

따라서, S = N 교차 검증법은 데이터 포인트 하나만 남겨두고(leave-one-out) 모델을 훈련시키는 테크닉입니다.

그림에서 빨간색 블록으로 표시되어 있는 것이 남겨 두는 집합이 되며, 이를 이용해서 검증을 진행합니다.

그리고 최종 성능 점수를 도출할 때는 S번의 실행에서의 성능 점수를 평균 내어서 도출하게 됩니다.

교차 검증법의 주요 단점 중 하나는 S의 수가 늘어남에 따라서 모델 훈련의 시행 횟수가 함께 늘어난다는 점입니다. 이는 훈련 자체가 계산적으로 복잡할 경우에 문제가 될 수 있습니다. 

분리된 데이터를 활용하여 성능을 측정하는 교차 검증법의 또 다른 문제점은, 한 가지 모델에 여러 가지 복잡도 매개변수가 있을 경우(예를 들면 여러 종류의 정규화 매개변수)에 발생합니다. 여러 매개변수들의 조합들을 확인해 보기 위해서는 최악의 경우 매개변수 숫자에 대해 기하급수적인 수의 훈련 실행이 필요할 수 있습니다.

따라서 이를 통해, 이보다 더 나은 방식이 필요하다는 것을 알 수 있습니다. 이상적인 방식에서는 훈련 집합만을 활용하여 여러 종류의 hyperparameter와 각 모델 종류에 대한 비교를 한 번의 훈련 과정동안 시행할 수 있어야 합니다.

이를 위해서는 오직 훈련 집합만을 활용하는 성능 척도가 필요합니다. 또한, 이 척도는 과적합으로 인한 편향으로부터 자유로워야 합니다.

역사적으로 다양한 '정보 기준(information criteria)'들이 최대 가능도 방법의 편향 문제에 대한 대안으로 제시되어 왔으며, 이는 더 복잡한 모델에서 과적합이 일어나지 않도록 하는 페널티항을 추가하는 방식이였습니다.

예를 들어, 아카이케 정보량 기준(akaike information criterion, AIC)는 다음의 식 1.73의 값이 가장 큰 모델을 선택하는 방식입니다.

여기서 $p(D|\bf{w_{ML}}$$)$은 가장 잘 피팅된 로그 가능도이며, $M$은 모델의 수정 가능한 매개변수의 수 입니다.

베이지안 정보 기준(Bayeseian information criterion, BIC)은 AIC의 약간 변형된 버전인데 이에 대해서는 4.4.1절에서 논의할 예정입니다. 

이러한 기준들은 모델 매개변수들의 불확실성을 고려하지 않으며, 또한 실제 적용에서 간단한 모델을 선택하는 경향이 있습니다.

해당 글에서는 Chapter 1. (2)인 확률론에서 1.2.4인 가우시안 분포부터를 다루고 있습니다.

1.2.4 가우시안 분포

이번 장에서는 정규 분포(normal distribution)라고도 불리는 가우시안 분포(Gaussian distribution)에 대해 살펴봅니다.

단일 실수 변수 $x$에 대해서 가우시안 분포는 다음과 같이 정의됩니다.

식 1.46은 두 개의 매개변수 $\mu$와 $\sigma^2$에 의해 통제됩니다. $\mu$는 평균(mean), $\sigma^2$는 분산(variance)입니다.

분산의 제곱근 값인 $\sigma$는 표준 편차(standard deviation)이라고 불립니다. 또한, 분산의 역수에 해당하는 $\beta$ = $1/\sigma^2$는 정밀도(precision)이라고도 합니다. 매개변수들이 왜 이런 이름을 가지는지에 대해서 곧 살펴봅니다. 가우시안 분포를 그리면 그림 1.13처럼 나타납니다.

종 모양의 그림이 되고, 중심이 $\mu$이며 폭이 $2\sigma$인 그래프가 됩니다.

식 1.46으로부터, 가우시안 분포가 다음의 성질을 만족함을 확인할 수 있습니다.

또한, 다음의 성질도 만족합니다.

따라서, 식 1.46은 확률 밀도의 두 가지 조건을 만족시킵니다.

가우시안 분포를 따르는 임의의 $x$에 대한 함수의 기댓값을 구할 수 있습니다. 특히 $x$의 평균값은 다음과 같습니다.

이를 통해 평균값 매개변수 $\mu$가 $x$의 기댓값과 동일함을 확인할 수 있습니다. 이와 비슷하게 $x$에 대한 이차 모멘트는 다음과 같습니다.

식 1.49와 식 1.50으로부터 $x$의 분산을 다음과 같이 계산할 수 있습니다.

$\sigma^2$가 분산임을 확인할 수 있습니다. 분포의 최댓값을 최빈값(mode)이라 하는데, 가우시안 분포의 경우에는 최빈값과 평균값이 동일합니다.

관측된 데이터 $\bf{x}$ = ($x_1$, ... $x_N$)$^T$를 살펴봅니다. 이는 관측된 $N$개의 스칼라 변수 $x$를 지칭합니다. 평균값 $\mu$와 분산 $\sigma^2$를 가지는 가우시안 분포에서 관측값들을 독립적으로 추출한다고 가정합니다.

데이터 집합으로부터 이 매개변수들을 결정하는 것이 우리의 현재 목표입니다.

같은 분포에서 독립적으로 추출된 데이터 포인트들을 독립적이고 동일하게 분포(independent and identically distributed, i.i.d)되었다고 한다. 앞에서 두 독립 사건의 결합 확률은 각 사건의 주변 확률의 곱이라고 하였으므로, i.i.d인 우리의 데이터 집합 $\bf{x}$은 $\mu$와 $\sigma^2$가 주어졌을 때의 조건부 확률을 다음과 같이 적을 수 있습니다.

$\mu$와 $\sigma^2$의 함수로 보면 이 식은 가우시안 분포의 가능도 함수에 해당합니다.  이전에 우리가 가능도 함수를 $p(D|\bf{w}$$)$로 표현했던 것을 생각해보면, 여기서 $\bf{w}$는 매개변수들의 집합이었으며 가우시안 분포에서는 이것이 바로 $\mu$와 $\sigma^2$가 됩니다. 

식 1.53를 그림으로 표현한 것이 바로 그림 1.14 입니다.

그림 1.14에서 빨간색 곡선이 바로 가능도 함수입니다. 여기서 $x$축에 있는 검은색 포인트는 ${x_n}$을 값으로 가지는 데이터 집합을 지칭하며, 식 1.53으로 주어진 가능도 함수는 파란색 포인트의 값들의 곱에 해당합니다. 평균값과 분산을 조정하여 해당 곱을 최대화함으로써 가능도를 최대화할 수 있습니다.

관측된 데이터 집합을 바탕으로 확률 분포의 매개변수를 결정하는 표준적인 방법 중 하나는 가능도 함수를 최대화하는 매개변수를 찾는 것입니다. 가능도 함수를 그냥 사용하지 않고 여기에 로그를 취해서 사용하게 되는데, 로그 함수는 변수에 대해 단조 증가하는 함수이므로 로그를 취한 후 최댓값을 찾는 것이 결국 원래 함수의 최댓값을 찾는 것과 동일하기 때문입니다. 로그를 취함으로써 추후 수학적 분석이 간단해지고, 컴퓨터 계산의 수치적인 측면에서도 도움이 된다고 합니다.

식 1.46과 식 1.53에 따라 로그 가능도 함수를 다음과 같이 적을 수 있습니다.

이에 대해서 $\mu$로 미분했을 때 0이 나오는 최댓값을 찾게 되면 다음의 최대 가능도 해 $\mu_{ML}$를 찾을 수 있습니다.

이는 관찰된 값 {$x_n$}들의 평균인 표본 평균(sample mean)입니다. 이와 비슷한 방식으로 식 1.54의 최댓값을 $\sigma^2$에 대해서 찾으면 분산에 대한 최대 가능도 해를 다음과 같이 찾을 수 있습니다.

이는 표본 평균에 대해 계산된 표본 분산(sample variance)입니다. 가우시안 분포의 경우는 $\mu$에 대한 해가 $\sigma^2$에 대한 해와 연관되어 있지 않습니다. 따라서 식 1.55를 먼저 계산하고 이 결과를 사용해서 식 1.56를 계산할 수 있습니다.

이 장의 뒷부분과 책의 나머지 부분에서 최대 가능도 방법의 한계점에 관해 더 자세히 이야기할 것이지만, 여기서는 우리가 현재 다루고 있는 단변량 가우시안 분포를 기준으로 최대 가능도 방법을 통해 계산한 매개변수값이 어떤 문제를 가지고 있는지 살펴보겠습니다.

최대 가능도 방법은 구조적으로 분포의 분산을 과소평가하게 되는데, 이는 편향(bias)이라고 불리는 현상의 예시로써 다항식 곡선 피팅에서 살펴본 과적합 문제와 연관되어 있습니다. 

통계에서 편향이란, 추정량과 모수의 차이를 의미합니다. 예를 들어서, 실제로 평균이 1이고 분산이 0인 가우시안 분포에서 샘플을 뽑는다고 가정합니다. 이때, 샘플을 여러 번 뽑는 과정을 통해서 평균이 1이고 분산이 1이라고 추정했습니다. 이렇게 된다면, 분산에 편향이 발생한 것이다 라고 생각하시면 됩니다.

최대 가능도 해인 $\mu_{ML}$과 $\sigma^2_{ML}$는 데이터 집합인 $x_1, ...x_N$의 함수입니다. $\mu$와 $\sigma^2$를 모수로 하는 가우시안 분포에서 추출된 각 데이터 집합의 값에 대해 이들의 기댓값을 고려해봅시다. 

책에는 너무 당연하다는 식으로 써있지만, 갑자기 왜 이들의 기댓값을 고려해보는지에 대해서 생각해보았습니다.

우리가 표본추출을 통해서 모집단의 평균을 구할 때, 표본평균의 평균을 구하게 됩니다.

또, 표본추출을 통해서 모집단의 분산을 구할 때, 표본분산의 평균을 구하게 됩니다.

따라서, 이와 같은 원리로 식 1.57은 표본평균($\mu_{ML}$)의 평균을 구해서 모집단의 평균을 추정한 것이고

식 1.58은 표본분산($\sigma^2_{ML}$)의 평균을 구해서 모집단의 분산을 추정한 것입니다.

따라서 평균적으로 최대 가능도 추정을 이용하면 평균은 올바르게 구할 수 있지만, 분산은 ($N$ - 1)/$N$만큼 과소평가하게 됩니다. 이 결과에 대한 직관적인 설명은 그림 1.15에서 확인할 수 있습니다.

그림 1.15를 보면, 최대 가능도 방법을 이용해서 가우시안 분포의 분산을 구하고자 할 때 어떻게 편향이 생기는지를 확인할 수 있습니다. 녹색 곡선은 데이터가 만들어진 실제 가우시안 분포를 나타내며, 세 개의 빨간색 곡선은 세 개의 데이터 집합에 대해 식 1.55와 식 1.56의 최대 가능도 방법을 이용해서 피팅한 가우시안 분포를 나타냅니다.

각각의 데이터 집합은 두 개의 데이터 포인트를 포함하고 있으며, 파란색 원으로 표시되어 있습니다. 세 개의 데이터 집합에 대해 평균을 내면 평균값은 올바르게 계산되지만, 분산 값은 실제 평균값이 아닌 표본 평균값을 기준으로 분산을 계산하기 때문에 구조적으로 과소평가될 수밖에 없습니다.

즉, 분산 값을 계산할 때 실제 평균값(해당 그림에서 가장 중앙에 뾰족 튀어나온 지점)을 기준으로 해서 분산을 계산하는 것이 아닌, 표본 평균값(해당 빨간색 그래프의 평균값)을 기준으로 분산을 계산하므로 실제 분산 값에 비해서 더 적은 값으로 계산된다는 것입니다.

직접 손으로 계산해보지 않더라도, 중앙에 뾰족 튀어나온 지점을 기준으로 분산을 계산하는 것과, 해당 빨간색 그래프의 평균값을 기준으로 분산을 계산하는 것에는 차이가 있다는 것이 느껴지실 것입니다.

식 1.58로부터 다음 식 1.59에서 보이는 분산 추정치는 비편향임을 알 수 있습니다.

데이터 포인트의 개수인 $N$이 커질수록 최대 가능도 해에서의 편향치는 점점 줄어들게 됩니다. 만약 $N$이 무한대로 갈 경우에는 최대 가능도 해의 분산과 데이터가 추출된 원 분포의 분산이 같아짐을 확인할 수 있습니다. 실제 적용 사례에서는 $N$이 아주 작은 경우가 아니면 이 편향은 그렇게까지 큰 문제는 되지 않습니다. 

하지만 이 책 전반에 걸쳐 많은 매개변수를 포함한 복잡한 모델에 대해 살펴볼 것인데, 이 경우 최대 가능도 방법과 연관된 편향 문제는 더욱 심각해집니다. 최대 가능도 방법의 편향 문제는 우리가 앞에서 살펴본 다항식 곡선 피팅에서의 과적합 문제의 근본적인 원인에 해당합니다.

1.2.5 곡선 피팅

앞에서는 다항식 곡선 피팅 문제를 오차 최소화의 측면에서 살펴보았습니다. 여기서는 같은 곡선 피팅 문제를 확률적 측면에서 살펴봄으로써 오차 함수와 정규화에 대한 통찰을 얻어봅니다. 또한, 완전한 베이지안 해결법을 도출하는 데 도움이 될 것입니다.

곡선 피팅 문제의 목표는 $N$개의 입력값 $\bf{x}$ = ($x_1, ... x_N$)$^T$과 해당 표적 값 $\bf{t}$ = ($t_1, ... t_N$)$^T$가 주어진 상황에서 새로운 입력 변수 $x$가 주어졌을 때 그에 대한 타깃 변수 $t$를 예측해 내는 것입니다.

확률 분포를 이용해서 타깃 변수의 값에 대한 불확실성을 표현할 수 있습니다. 이를 위해서 주어진 $x$값에 대한 $t$값이 $y(x, \bf{w}$$)$를 평균으로 가지는 가우시안 분포를 가진다고 가정합니다. 여기서 $y(x, \bf{w}$$)$는 앞의 식 1.1에서 주어졌던 다항식 곡선입니다. 이를 바탕으로 다음의 조건부 분포를 적을 수 있습니다. 

여기서 사용한 $\beta$는 정밀도 매개변수로 분포의 분산의 역수에 해당합니다. 이 식을 도식화해 놓은 것이 바로 그림 1.16입니다.

해당 그림에서 파란색 점과 빨간색 점은 설명을 위해 제가 그린 점입니다.

일단 빨간색 곡선으로 그려진 것은 우리가 데이터를 통해서 학습시킨 다항식 곡선이라고 보시면 됩니다. 그림에서는 $y(x, \bf{w}$$)$라고 표현되어 있습니다.

그리고 그림에서 $y(x_0, w)$라고 표시된 것은, $x$의 값이 $x_0$일 때, 다항식 곡선을 이용해서 예측된 prediction 값이라고 보시면 되겠습니다.

우리는 현재 주어진 $x$ 값에 대한 $t$값이 이 예측된 값을 평균으로 가지는 가우시안 분포를 가진다고 가정하기 때문에, 그림이 현재 형광 녹색으로 표시된 지점을 기준으로 파란색으로 그려진 가우시안 분포가 그려진 것입니다.

그렇다면, 해당 그림에서 특정 지점(데이터 포인트)에 대해서 조건부 확률 값을 어떻게 구할까요?

예를 들어서, 데이터가 $x$ 값이 $x_0$일 때, 파란색 점이 타깃 변수(정답 값) $t$의 위치라고 하겠습니다. 

그렇다면 해당 타깃 변수의 값에 대한 조건부 확률 값은, 파란색 가우시안 곡선으로 그려진 $p(t|x_0, w, \beta)$로 계산되는 값이 될 것이며, 그림 상에서 빨간색 점이 됩니다.  

가우시안 분포의 특성상, 타깃 변수의 값이 가우시안 분포의 평균과 동일할 때, 조건부 확률 값이 가장 커질 것이며 타깃 변수의 값과 가우시안 분포의 평균이 멀어질수록 조건부 확률 값이 작아질 것입니다. 

이제 훈련 집합 {$\bf{x}, \bf{t}$}를 바탕으로 최대 가능도 방법을 이용해 알려지지 않은 매개변수 $\bf{w}$와 $\beta$를 구해보도록 합시다. 만약 데이터가 식 1.60의 분포에서 독립적으로 추출되었다고 가정하면, 가능도 함수는 다음과 같이 주어집니다.

앞에서와 마찬가지로 가능도 함수에 로그를 취해 그 최댓값을 구하는 것이 편리합니다. 식 1.46의 가우시안 분포를 대입해 넣으면 다음과 같은 형태의 로그 가능도 함수를 얻게 됩니다.

첫 번째로 다항식 계수 $\bf{w_{ML}}$의 최대 가능도 해를 구해봅니다.

$\bf{w}$에 대해 식 1.62를 최대로 만드는 값을 구하면 됩니다. 이 과정에서 식 1.62의 오른쪽 변의 마지막 두 항은 관련이 없으므로 제외합니다. 또한, 로그 가능도에 양의 상수를 곱해도 상관없으므로, 맨 앞의 계수를 1/2로 바꿔줍니다. 마지막으로 로그 가능도를 최대화하는 대신에 로그 가능도의 음의 값을 취한 후, 이를 최소화할 수 있습니다. 이를 식으로 표현하자면 $min \frac{1}{2} \sum_{n=1}^N\left\{y(x_n, w)-t_n\right\}^2$이 됩니다.

결과적으로 $\bf{w}$를 구하는 경우에 가능도 함수를 최대화하는 것은 식 1.2에서 나왔던 제곱합 오차 함수를 최소화하는 것과 같다는 것을 알 수 있습니다. 노이즈가 가우시안 분포를 가진다는 가정하에 가능도 함수를 최대화하는 시도의 결과로 제곱합 오차 함수를 유도할 수 있는 것입니다.

마찬가지로 가우시안 조건부 분포의 정밀도 매개변수 $\beta$를 결정하는 데도 최대 가능도 방법을 사용할 수 있으며, 식 1.62를 $\beta$에 대해 최대화하면 다음의 식이 도출됩니다.

단순 가우시안 분포의 경우와 마찬가지로 평균값에 해당하는 매개변수 벡터 $\bf{w_{ML}}$을 먼저 구한 후에 이를 사용하여 정밀도 $\beta_{ML}$를 구할 수 있습니다.

매개변수 $\bf{w}$와 $\beta$를 구했으니 이제 이를 바탕으로 새로운 변수 $x$에 대해 예측값을 구할 수 있습니다. 이제 우리는 확률 모델을 사용하고 있으므로 예측값은 전과 같은 하나의 점 추정값이 아닌 $t$에 대한 예측 분포(predictive distribution)으로 표현될 것입니다. 최대 가능도 매개변수들을 식 1.60에 대입하면 다음을 얻을 수 있습니다.

이를 설명해보자면 다음과 같이 설명할 수 있을 것 같습니다.

input value $x$에 대해서, 피팅된 곡선(곡선의 가중치 $\bf{w_{ML}}$)를 이용하면 예측값을 구할 수 있습니다.

이 예측값을 평균으로, $\beta^{-1}_{ML}$를 분산으로 하는 가우시안 분포를 t가 따른다는 것입니다. 그래서 예측 분포라는 용어를 사용하여 식 1.64를 설명한 것이라고 이해를 해볼 수 있을 것 같습니다.

베이지안 방식을 향해 한 걸음 더 나아가 보겠습니다. 이를 위해 다항 계수 $\bf{w}$에 대한 사전 분포를 도입할 것입니다. 문제의 단순화를 위해 다음 형태를 지닌 가우시안 분포를 사용해봅니다.

 여기서 $\alpha$는 분포의 정밀도이며, $M + 1$은 $M$차수 다항식 벡터 $\bf{w}$의 원소의 개수입니다. ($M$차수 이면 마지막 상수항 $w_0$가 존재하므로 $M +1$개가 되는 것으로 생각이 됩니다.) $\alpha$와 같이 모델 매개변수의 분포를 제어하는 변수들을 초매개변수(hyperparameter)라 합니다. 베이지안 정리에 따라서 $\bf{w}$의 사후 분포는 사전 분포와 가능도 함수의 곱에 비례합니다.

이제 주어진 데이터에 대해 가장 가능성이 높은 $\bf{w}$를 찾는 방식으로 $\bf{w}$를 결정할 수 있습니다. 바꿔 말하면 사후 분포를 최대화하는 방식으로 $\bf{w}$를 결정할 수 있다는 것입니다. 이 테크닉을 최대 사후 분포(maximum posterior, MAP)라고 합니다. 식 1.66에 대해 음의 로그를 취한 식 1.62, 식 1.65와 결합하면 사후 확률의 최댓값을 찾는 것이 다음 식 값의 최솟값을 찾는 것과 동일함을 알 수 있습니다.

식 1.66에 음의 로그를 취하면

식 1.62와 식 1.65의 합으로 구성됩니다. 여기서 우리는 적절한 $\bf{w}$를 구하는 것이 목표이므로, $\frac{N}{2}ln\beta$ 등의 상수항들을 제외해줍니다.

그러고 나서 -를 곱해줘서 최소화 문제로 바꿔주면, 식 1.67을 최소화하는 문제로 바뀌게 됩니다.

이처럼 사후 분포를 최대화하는 것이 정규화 매개변수가 $\lambda = \alpha/\beta$로 주어진 식 1.4의 정규화된 제곱합 오차 함수를 최소화하는 것과 동일함을 확인할 수 있습니다.

1.2.6 베이지안 곡선 피팅

비록 사전 분포 $p(\bf{w}$|$\alpha$)를 포함시키긴 했지만, 여전히 $\bf{w}$에 대해서 점 추정을 하고 있기 때문에 아직은 완벽한 베이지안 방법론을 구사한다고 말할 수 없습니다. 완전한 베이지안적 접근을 위해서는 확률의 합의 법칙과 곱의 법칙을 일관적으로 적용해야 합니다. 이를 위해서는 모든 $\bf{w}$ 값에 대해서 적분을 시행해야 합니다. 이러한 주변화(marginalization)가 패턴 인식에서의 베이지안 방법론의 핵심입니다. 

곡선 피팅 문제의 목표는 훈련 집합 데이터 $\bf{x}$와 $\bf{t}$가 주어진 상황에서 새로운 변수 $x$에 대한 타깃 값 $t$를 예측하는 것입니다. 이 목표를 위해서 예측 분포 $p(t|x, \bf{x}, \bf{t}$$)$를 구해봅시다. 여기서는 매개변수 $\alpha$와 $\beta$는 고정되어 있으며, 미리 알려졌다고 가정합니다.

단순히 말하자면 베이지안 방법은 단지 확률의 합과 곱의 법칙을 계속적으로 적용하는 것입니다. 이를 통해 예측 분포를 다음과 같은 형태로 적을 수 있습니다.

여기서 $p(t|x, \bf{w}$$)$는 식 1.60에서 주어진 것입니다. 간략한 표기를 위해 $\alpha$와 $\beta$에 대한 종속성은 생략했습니다.

$p(w|\bf{x}, \bf{t}$$)$는 매개변수들에 대한 사후 분포이며, 식 1.66의 오른쪽 변을 정규화함으로써 구할 수 있습니다.

3.3절에서는 곡선 피팅 예시와 같은 문제의 경우 사후 분포가 가우시안이며, 해석적으로 계산할 수 있다는 것에 대해서 살펴봅니다. 이와 비슷하게 식 1.68의 적분을 시행하면 예측 분포가 다음의 식 1.69와 같이 가우시안 분포로 주어진다는 것을 알 수 있습니다.

여기서 평균과 분산은 다음과 같습니다. 

행렬 $\bf{S}$는 다음처럼 주어집니다.

$\bf{I}$는 단위 행렬이며, $\phi(x)$는 각각의 원소가 $i = 0, ..., M$에 대해 $\phi_i(x) = x^i$인 벡터입니다. 

아마 이거 읽는 분들도 이게 왜 나왔을까... 궁금하시겠지만 따로 뭐 도출 과정이나 이런 게 책에 없어서 왜 이렇게 계산되었는지는 알 수가 없었네요 ㅠㅠ

식 1.69를 살펴보면, 예측 분포의 평균과 분산이 $x$에 종속되어 있음을 알 수 있습니다. 타깃 변수의 노이즈로 인한 예측값 $t$의 불확실성이 식 1.71의 첫 번째 항에 표현되어 있습니다. 이 불확실성은 식 1.64의 최대 가능도 예측 분포에서 $\beta^-1_{ML}$로 이미 표현되었습니다. 하지만 식 1.71의 두 번째 항은 $\bf{w}$의 불확실성으로부터 기인한 것이며, 베이지안 접근법을 통해 구해진 것입니다. 

그림 1.17은 베이지안적 방법을 통해 구한 $M= 9$ 다항식 곡선 피팅 문제의 예측 분포를 나타내는 그림입니다.

$\alpha = 5 \times 10^{-3}$, $\beta = 11.1$을 사용하였습니다. 빨간색 선은 예측 분포의 평균값을, 그리고 빨간색 영역은 평균값으로부터 $\pm1$ 표준 편찻값을 가지는 부분을 표현한 것입니다. 녹색선은 해당 데이터를 만들 때 사용되었던 $sin(2\pi x)$를 나타낸 그림입니다. 파란색 동그라미인 데이터 포인트는 녹색선을 기준으로 약간의 노이즈를 포함시켜서 만들어낸 데이터라고 보시면 되겠습니다.

최대한 이해해보려고 노력하면서 읽긴 하지만, 역시나 쉽진 않은 책이라는 게 느껴집니다.

특히 조금 간단한 예시를 들었으면 좋았을 텐데... 너무 자명하다는 식으로 쓴 내용들이 많아 이해가 쉽진 않군요 ㅠㅠ

다음 장 내용도 이어서 보도록 하겠습니다.

패턴 인식 분야에서 주요한 콘셉트 중 하나는 바로 불확실성입니다. 불확실성은 측정할 때의 노이즈를 통해서도 발생하고, 데이터 집합 수가 제한되어 있다는 한계점 때문에도 발생합니다. 확률론은 불확실성을 계량화하고 조작하기 위한 이론적인 토대를 마련해 주며, 패턴 인식 분야의 중요한 기반이기도 합니다. 1.5절에서 논의할 의사 결정 이론과 이번 절의 확률론을 함께 활용하면, 주어진 정보가 불확실하거나 완전하지 않은 제약 조건하에서도 최적의 예측을 시행할 수 있게 됩니다.

하나의 예시를 들어보겠습니다. 

한 개의 빨간색 상자와 한 개의 파란색 상자가 있고, 빨간색 상자에는 두 개의 사과와 여섯 개의 오렌지, 파란색 상자에는 한 개의 오렌지와 세 개의 사과가 있습니다. 랜덤 하게 상자 하나를 골라 임의로 과일 하나를 꺼내고, 어떤 과일인지 확인한 후 꺼냈던 상자에다 도로 집어넣는 상황을 생각해봅니다. 빨간색 상자를 고를 확률은 40%, 파란색 상자를 고를 확률은 60%라고 합니다. 상자 안에서 각각의 과일을 고를 확률은 동일하다고 가정합니다.

이 예시에서 상자는 확률 변수이며, 확률 변수 $B$라고 지칭합니다. 확률 변수 B는 $r$(빨간색 상자)와 $b$(파란색 상자) 두 개의 값을 가질 수 있습니다.

과일 또한 확률 변수이며, 여기서는 $F$로 지칭합니다. 확률 변수 F는 $a$(사과) 또는 $o$(오렌지)를 값으로 가질 수 있습니다.

어떤 사건의 '확률'을 무한 번 시도한다고 가정했을 때 어떤 특정 사건이 일어나는 횟수를 전체 시도의 횟수로 나눈 것으로 정의해본다면, $p(B=r)$ = 4/10이고, $p(B=b)$ = 6/10 입니다.

이러한 확률 말고, 조금 더 복잡한 확률에 대해서 알아보기 위해 먼저 확률의 두 가지 기본 법칙인 합의 법칙(sum rule)과 곱의 법칙(product rule)에 대해서 먼저 살펴봅니다.

확률의 법칙을 설명하기 위해, 그림 1.10의 예시를 고려해보겠습니다.

해당 예시에서는 $X$와 $Y$라는 두 가지 확률 변수를 생각합니다. $X$는 $x_i(i = 1, ..,M)$ 중 아무 값이나 취할 수 있고, $Y$는 $y_j(j = 1, ... L)$ 중 아무 값이나 취할 수 있다고 가정합니다. 여기서 $M$ = 5이고, $L$ = 3입니다.

또한, $X$와 $Y$ 각각에서 표본을 추출하는 시도를 $N$번 한다고 합니다. 그리고 $X = x_i, Y = y_j$인 시도의 개수를 $n_{ij}$로 표현합니다. 그리고 $Y$의 값과는 상관없이 $X = x_i$인 시도의 숫자를 $c_i$로, $X$의 값과는 상관없이 $Y = y_j$인 시도의 숫자를 $r_j$로 표현할 것입니다.

$X$가 $x_i$, $Y$가 $y_j$일 확률을 $p(X = x_i, Y = y_j)$로 적고, 이를 $X = x_i, Y = y_j$일 결합 확률(joint probability)이라고 칭합니다. 이는 $i, j$ 칸에 있는 포인트의 숫자를 전체 포인트들의 숫자로 나눠서 구할 수 있는데요, 따라서 다음 식 1.5와 같이 표현할 수 있습니다.

여기서는 $lim N -> \infty$를 가정합니다. 비슷하게 $Y$ 값과 무관하게 $X$가 $x_i$값을 가질 확률을 $p(X = x_i)$로 적을 수 있으며, 이는 $i$열에 있는 포인트들의 숫자를 전체 포인트들의 숫자로 나눔으로써 구할 수 있습니다. 이를 식으로 표현하면 식 1.6로 표현할 수 있습니다.

그림 1.10에서 $i$열에 있는 사례의 숫자는 해당 열의 각 칸에 있는 사례의 숫자 합입니다. 이는 $c_i = \sum_j n_{ij}$로 표현 가능합니다. 따라서, 식 1.5와 식 1.6을 바탕으로 식 1.7을 도출해 낼 수 있습니다.

이것이 바로 확률의 합의 법칙(sum rule)입니다. 때때로 $p(X= x_i)$는 주변 확률(marginal probability)이라고 불립니다. 

합의 법칙을 말로 좀 풀어서 생각해보자면, 어떤 주변 확률을 구하려면 결합 확률을 이용해서 구할 수 있는데 결합 확률에 포함된 다른 확률 변수들의 모든 경우를 다 더했을 때 구할 수 있다 정도로 이해해볼 수 있겠습니다.

훨씬 단순한 예시를 하나 들자면... 상의 2가지 하의 3가지가 있으면 우리가 입을 수 있는 모든 옷의 경우의 수는 6가지가 될 것인데요. 여기서 1번 상의를 입게 될 확률은 결국 1번 상의 + 1번 하의 / 1번 상의 + 2번 하의 / 1번 상의 + 3번 하의를 입을 확률을 더해야 된다는 것이죠. 즉, 내가 어떤 확률 변수에 대한 주변 확률을 구하려면, 결합 확률에 포함된 다른 확률 변수들의 모든 케이스를 다 더했을 때 구할 수 있다는 것입니다.

$X = x_i$인 사례들만 고려해 봅시다. 그들 중에서 $Y = y_j$인 사례들의 비율을 생각해 볼 수 있고, 이를 확률 $p(Y = y_j | X = x_i)$로 적을 수 있습니다. 이를 조건부 확률(conditional probability)이라고 부릅니다. 이 경우엔 $X = x_i$가 주어졌을 경우 $Y = y_j$일 조건부 확률을 의미합니다. 이는 $i$행에 있는 전체 포인트 수와 $i, j$칸에 있는 포인트 수의 비율을 통해서 계산할 수 있습니다.

일반 확률과 조건부 확률의 차이라고 한다면, 일반 확률은 시행 횟수 N으로 나누지만 조건부 확률은 시행 횟수 모두를 고려하는 것이 아닌, 조건에 해당하는 경우(위 수식 1.8에서는 $X = x_i$인 경우)만 고려하기 때문에 확률을 구할 때 분모의 값이 달라지게 됩니다. 이 부분이 가장 핵심이라고 생각합니다.

식 1.5, 식 1.6, 식 1.8에서 다음의 관계를 도출해 낼 수 있습니다.

이것이 바로 확률의 곱의 법칙(product rule)입니다.

이를 말로 풀어서 설명하자면, A와 B의 결합 확률은 A를 선택할 확률과 A를 선택했다고 생각했을 때 B를 선택할 확률의 곱이 된다는 것입니다.

제가 앞에 들었던 상의 2가지, 하의 3가지의 간단한 예시로 생각해보겠습니다. 1번 상의와 1번 하의를 입는 확률을 생각해본다면, 확률은 1/6이 됩니다. 전체 경우의 수 6가지 중 1가지가 되니까요.

$p(Y = y_j | X = x_i)$를 생각해보겠습니다. $X$를 상의, $Y$를 하의라고 생각하면 이는 1번 상의를 입는다는 가정 하에 1번 하의를 입을 확률입니다. 1번 상의를 입는다고 가정하면, 하의는 1번 2번 3번 총 3가지밖에 없으므로 이는 1/3이 됩니다. 

$p(X = x_i)$를 생각해보겠습니다. 상의는 2가지가 있으므로, 1번 상의를 입을 확률은 1/2가 됩니다.

따라서 식 1.9에서 정의한 것처럼, 1/6 = 1/3 * 1/2 가 성립함을 확인할 수 있습니다.

지금까지 얘기한 확률의 두 법칙을 조금 더 간단한 표현법을 사용해 표현하면 다음과 같습니다.

곱의 법칙과 대칭성 $p(X, Y) = p(Y, X)$로부터 조건부 확률 간의 관계인 다음 식을 도출해낼 수 있습니다.

식 1.12는 머신 러닝과 패턴 인식 전반에 걸쳐서 아주 중요한 역할을 차지하고 있는 베이즈 정리(Bayes' theorem)입니다. 위에서 언급한 합의 법칙을 사용하면 베이지안 정리의 분모를 분자에 있는 항들로 표현할 수 있습니다.

베이지안 정리의 분모는 정규화 상수로 볼 수 있습니다. 즉, 식 1.12의 왼쪽 항을 모든 $Y$값에 대하여 합했을 때 1이 되도록 하는 역할인 것이죠.

이제 원래 논의했던 과일 상자 예시로 돌아가 봅시다. 빨간색 상자를 선택하거나 파란색 상자를 선택하는 확률은 다음과 같습니다.

위의 식 1.14와 식 1.15의 합이 1을 만족시킨다는 것을 확인할 수 있습니다.

상자가 주어졌을 때 사과 또는 오렌지를 선택할 확률 네 가지를 다음과 같이 적을 수 있습니다.

마찬가지로, 이 확률들은 정규화되어 있기 때문에 다음 식 1.20과 식 1.21을 만족시킵니다.

이제 확률의 합의 법칙과 곱의 법칙을 적용하여 사과를 고를 전체 확률을 계산할 수 있습니다.

여기에 다시 합의 법칙을 적용하면 $p(F = 0)$ = 1 - 11/20 = 9/20입니다.

어떤 한 종류의 과일을 선택했는데 그것이 오렌지고, 이 오렌지가 어떤 상자에서 나왔는지를 알고 싶다고 가정해봅니다. 이는 베이지안 정리를 적용해서 구할 수 있습니다.

합의 법칙에 따라 $p(B = b | F = o)$ = 1 - 2/3 = 1/3이 됩니다.

베이지안 정리를 다음과 같이 해석할 수 있습니다.

만약 어떤 과일이 선택되었는지를 알기 전에 어떤 박스를 선택했냐고 묻는다면 그 확률은 $p(B)$일 것입니다. 이를 사전 확률(prior probability)이라고 부릅니다. 왜냐하면 어떤 과일이 선택되었는지 관찰하기 '전'의 확률이기 때문이죠. 선택된 과일이 오렌지라는 것을 알게 된다면 베이지안 정리를 활용하여 $p(B|F)$를 구할 수 있습니다. 이는 사후 확률(posterior probability)이라고 부를 수 있는데, 이는 사건 $F$를 관측한 '후'의 확률이기 때문입니다.

이 예시에서 빨간색 상자를 고를 사전 확률은 4/10이므로, 파란색 상자를 고를 확률이 더 높습니다. 하지만, 선택된 과일이 오렌지라는 것을 확인하고 난 후엔 빨간색 상자를 고를 사후 확률이 2/3입니다. 따라서 이제는 우리가 고른 상자가 빨간색이었을 확률이 더 높게 됩니다. 이는 빨간색 상자 안의 오렌지의 비율이 파란색 상자 안의 오렌지의 비율보다 높기 때문이죠. 오렌지를 골랐다는 증거가 충분히 강력하기 때문에 사전 지식을 뒤엎고 빨간색 상자를 골랐을 확률을 파란색 상자를 골랐을 확률보다 더 높게 만들어주는 것입니다.

$p(X, Y) = p(X)p(Y)$인 경우를 고려해 봅시다. 이처럼 각각의 주변 확률을 곱한 것이 결합 확률과 같을 경우 두 확률 변수를 독립적(independent)이라고 합니다. 곱의 법칙에 따라 $p(Y|X) = p(Y)$임을 알 수 있고, 이는 $X$가 주어졌을 때 $Y$의 조건부 확률은 실제로 $X$의 값과 독립적임을 확인할 수 있습니다. 

1.2.1 확률 밀도

지금까지는 이산적인 사건들을 바탕으로 확률을 알아보았는데, 이번에는 연속적인 변수에서의 확률에 대해 알아봅니다.

만약 실수 변수 $x$가 ($x$, $x+\delta x$) 구간 안의 값을 가지고 그 변수의 확률이 $p(x) \delta x$($\delta x$ -> 0 일 경우)로 주어진다면, $p(x)$를 $x$의 확률 밀도(probability density)라고 부릅니다. 이는 그림 1.12로 표현될 수 있습니다.

이때 $x$가 (a, b) 구간 사이의 값을 가질 확률은 다음과 같이 주어집니다.

단순하게, 확률 밀도 함수를 x = a부터 x = b까지 적분을 해주면 확률을 구할 수 있습니다.

확률은 양의 값을 가지고 $x$의 값은 실수축상에 존재해야 하므로, 다음 두 조건을 만족시켜야 합니다.

확률 분포 함수는 야코비안 인자로 인해 비선형 변수 변환 시에 일반적인 단순 함수와는 다른 방식으로 변화하게 됩니다. 예를 들어, $x = g(y)$의 변수 변환을 고려해 봅시다. 그러면 함수 $f(x)$는 $\tilde{f}(y)$ = $f(g(y))$가 됩니다. $x$의 확률 밀도 함수 $p_x(x)$와 새로운 변수 $y$의 확률 밀도 함수 $p_y(y)$를 살펴보면 둘이 다른 확률 밀도를 가진다는 것이 자명합니다. ($x$, $x + \delta x$) 범위에 속하는 관찰 값은 범위 ($y$, $y + \delta y$)로 변환될 것입니다. 이때 $p_x(x) \delta x $ $\simeq$ $p_y(y) \delta y $입니다. 따라서 다음과 같습니다.

이로부터, 확률 밀도의 최댓값은 어떤 변수를 선택하는지에 따라 달라짐을 알 수 있습니다.

책에는 식 1.27가 어떤 식으로 도출되는지에 대한 내용이 전혀 없어서, 왜 갑자기 저런 식이 나오는지 알 수 없었습니다. 이에 저는 관련된 내용을 찾아서 나름대로 정리를 해 보았는데요.

식 1.27가 나오는 과정이 궁금하시다면, 아래에 있는 더보기 부분을 누르셔서 확인하실 수 있습니다.

$x$가 ($-\infty, z$) 범위에 속할 확률은 누적 분포 함수(cumulative distribution function)로 표현될 수 있습니다.

누적 분포 함수는 곧 $-\infty$부터 $z$까지 확률밀도함수를 적분한 것을 의미합니다.

또, 그림 1.12에서 보인 것처럼 $P'(x) = p(x)$ 입니다.

만약 여러 개의 연속적인 변수 $x_1, ... x_D$가 주어지고 이 변수들이 벡터 $\bf{x}$로 표현될 경우에 결합 확률 밀도 $p(\bf{x}$$)$ = $p(x_1, .. x_D)$를 정의할 수 있습니다. 이 확률 밀도에서 $\bf{x}$가 포인트 $\bf{x}$를 포함한 극솟값 $\delta \bf{x}$에 포함될 확률은 $p(\bf{x}$$)$$\delta \bf{x}$로 주어집니다. 이 다변량 확률 밀도는 다음 조건을 만족해야 합니다.

식 1.30에서의 적분은 전체 $x$ 공간에 대해서 시행하는 것이며, 이산형 변수와 연속형 변수가 조합된 경우에 대해서도 결합 확률 분포를 고려하는 것이 가능합니다.

만약 $x$가 이산 변수일 경우 $p(x)$를 때때로 확률 질량 함수(probability mass function)라고 부르기도 합니다. 

연속 변수의 확률 밀도와 이산형 변수/연속형 변수가 조합된 경우의 확률 밀도에서도 합의 법칙, 곱의 법칙, 베이지안 정리를 적용할 수 있습니다. 예를 들어 $x, y$가 실수 변수인 경우, 합과 곱의 법칙은 다음과 같이 표현할 수 있습니다.

1.2.2 기댓값과 공분산

확률 밀도 $p(x)$ 하에서 어떤 함수 $f(x)$의 평균값은 기댓값(expectation)이라 하며, $E[f]$라 적습니다.

이산 분포의 경우 기댓값은 다음과 같이 주어집니다.

쉽게 생각하면, 각 $x$ 값에 대해 해당 확률을 가중치로 사용해서 가중치 x 값을 이용해서 가중 평균을 구하는 것입니다.

연속 변수의 경우에는 확률 밀도에 대해 적분을 해서 기댓값을 구합니다.

만약 유한한 $N$개의 포인트를 확률 분포 또는 확률 밀도에서 추출했다면, 포인트들의 합으로 기댓값을 근사할 수 있습니다.

다변수 함수의 기댓값을 구할 경우에는 어떤 변수에 대해 평균을 내는지를 지정해서 계산할 수 있습니다.

식 1.36은 함수 $f(x, y)$의 평균값을 $x$의 분포에 대해 구하라는 의미입니다. 이는 $y$에 대한 함수가 될 것입니다. ($x$에 대해서 계산한 것이므로)

또한, 조건부 분포에 해당하는 조건부 기댓값(conditional expectation)도 생각해 볼 수 있습니다.

$f(x)$의 분산(variance)은 다음과 같이 정의됩니다.

분산은 $f(x)$가 평균값으로부터 전반적으로 얼마나 멀리 분포되어 있는지를 나타내는 값입니다. 위 식을 전개하면 다음과 같이 표현할 수 있습니다.

고등학교 수학에서는 보통 제곱의 평균 - 평균의 제곱으로 많이 외우곤 합니다.

두 개의 확률 변수 $x$와 $y$에 대해서 공분산(covariance)은 다음과 같이 정의됩니다.

공분산은 $x$ 값과 $y$ 값이 얼마나 함께 같이 변동하는가에 대한 지표이며, 서로 독립이면 공분산은 0입니다.

두 확률 변수 $x$와 $y$가 벡터일 경우에는 공분산은 행렬이 됩니다.

1.2.3. 베이지안 확률

지금까지 우리는 확률을 '반복 가능한 임의의 사건의 빈도수'라는 측면에서 살펴보았습니다. 이러한 해석을 고전적(classical) 또는 빈도적(frequentist) 관점이라고 일컫는데요. 이보다 더 포괄적인 베이지안(Bayesian) 관점에 대해서 살펴봅니다. 베이지안 관점을 이용하면 확률을 이용해 불확실성을 정량화하는 것이 가능합니다.

어떤 불확실한 사건에 대해서 생각해보겠습니다. 예를 들어 '북극의 빙하가 이번 세기까지 다 녹아 없어진다'는 사건을 생각해보면, 이런 사건들은 여러 번 반복할 수 없습니다. 따라서 빈도적 관점에서 확률을 정의하는 것이 불가능합니다. 물론, 우리는 이러한 사건들에 대해 어떤 견해를 가지고 있긴 할 텐데요. 예를 들면 '북극의 얼음이 이 정도 속도로 녹는다'와 같은 의견이 될 수 있습니다.

만약 우리가 새로운 증거를 추가할 수 있다면 얼음이 녹는 속도에 대한 우리의 의견을 수정할 수 있을 것입니다. 이런 증거가 강력하다면 우리의 판단에 따라 취할 행동이 바뀔 수도 있죠. 예를 들어서, 얼음이 녹는 속도가 빠르다는 증거를 관측했다면 기후 변화를 늦추기 위해 노력할 수 있습니다. 이런 상황들에서 주어진 불확실성을 정량화하고, 새로운 증거가 주어질 때마다 불확실성을 수정하고 그 결과에 따라 최적의 선택을 내리고 싶을 때, 이것이 가능하게 해주는 방법론이 바로 확률의 베이지안 해석입니다. 즉 확률을 불확실성을 나타내는 도구로 활용하는 것이죠.

확률에 대한 개념을 더 일반적으로 확장하는 것은 패턴 인식 분야에서도 큰 도움이 됩니다. 1.1절의 다항 곡선 피팅 예시를 다시 생각해보겠습니다. 적합한 모델 매개변수 $\bf{w}$를 정하는 데 있어서 불확실성을 수치화하고 표현하려면 어떻게 해야 할까요? 이때 베이지안 관점을 사용하면 확률론의 다양한 장치들을 활용하여 $\bf{w}$와 같은 모델 매개변수의 불확실성을 설명할 수 있습니다. 더 나아가, 베이지안 관점은 모델 그 자체를 선택하는 데 있어서도 유용합니다.

앞의 과일 상자 예시에서 어떤 과일이 선택되었는지에 대한 관측 결과가 선택된 상자가 어떤 것이었을지에 대한 확률을 바꾸었던 것을 기억해 봅시다. 해당 예시에서 베이지안 정리는 관측값들을 이용하여 사전 확률을 사후 확률로 바꾸는 역할을 했습니다. 다항 곡선 피팅 예시의 매개변수 $\bf{w}$와 같은 값들을 추론해 내는 데 있어서도 비슷한 방식을 사용할 수 있습니다. 

일단, 첫 번째로 데이터를 관측하기 전의 $\bf{w}$에 대한 우리의 가정을 사전 확률 분포 $p(\bf{w})$로 표현할 수 있습니다. 관측된 데이터 $D$ = {${t_1, ... t_N}$}은 조건부 확률 $p(D|\bf{w})$로써 작용하게 됩니다. 이 경우 베이지안 정리는 다음의 형태를 띱니다.

$D$를 관측한 후의 $\bf{w}$에 대한 불확실성을 사후 확률 $p(\bf{w}$$|D)$로 표현한 것입니다.

베이지안 정리의 오른쪽에 있는 값 $p(D|\bf{w})$은 관측 데이터 집합 $D$를 바탕으로 계산됩니다. 이 값은 매개변수 벡터 $\bf{w}$의 함수로 볼 수 있으며, 가능도 함수(likelihood function)라고 불립니다. 가능도 함수는 각각의 다른 매개변수 벡터 $\bf{w}$에 대해 관측된 데이터 집합이 얼마나 '그렇게 나타날 가능성이 있었는지'를 표현합니다. 가능도 함수는 $\bf{w}$에 대한 확률 분포가 아니며, 따라서 $\bf{w}$에 대해 가능도 함수를 적분하여도 1이 될 필요가 없습니다.

가능도 함수에 대한 정의를 바탕으로 베이지안 정리를 다음처럼 적을 수 있습니다.

posterior = 사후 확률, likelihood = 가능도, prior = 사전 확률입니다.

식 1.44의 각 값은 전부 $\bf{w}$에 대한 함수입니다. 

식 1.43 오른쪽 변의 분모는 식 왼쪽 변의 사후 분포가 적절한 확률 분포가 되고 적분 값이 1이 되도록 하기 위한 정규화 상수입니다. 식 1.43 오른쪽 변의 분모는 다음과 같이 구할 수 있습니다.

가능도 함수 $p(D|\bf{w})$는 베이지안 확률 관점과 빈도적 확률 관점 모두에게 굉장히 중요한 역할을 합니다. 하지만 가능도 함수가 사용되는 방식은 양 접근법에서 근본적으로 다릅니다.

먼저, 빈도적 확률 관점에서는 $\bf{w}$가 고정된 매개변수로 여겨지며, 그 값은 어떤 형태의 '추정 값'을 통해서 결정됩니다. 그리고 추정에서의 오류는 가능한 데이터 집합들 $D$의 분포를 고려함으로써 구할 수 있습니다.

이와는 대조적으로 베이지안 확률 관점에서는 오직 하나의 데이터 집합 $D$만이 존재하고 매개변수의 불확실성은 $\bf{w}$의 확률 분포를 통해 표현됩니다.

빈도적 확률 관점에서 널리 사용되는 추정 값 중 하나는 바로 최대 가능도(maximum likelihood)입니다. 최대 가능도를 사용할 경우에 $\bf{w}$는 가능도 함수 $p(D|\bf{w})$를 최대화하는 값으로 선택됩니다. 머신러닝 문헌에서는 종종 음의 로그 가능도 함숫값을 오차 함수(error function)이라고 합니다. 음의 로그 함수는 단조 감소하는 함수이기 때문에 가능도의 최댓값을 찾는 것이 오차를 최소화하는 것과 동일하기 때문입니다.

빈도적 확률론자들이 오차를 측정하는 방법 중 하나가 바로 부트스트랩(bootstrap) 방법입니다. 원 데이터 집합이 $N$개의 데이터 포인트 $X$ = {$\bf{x_1}, ..., \bf{x_N}$}이라고 가정해봅니다. $\bf{X}$에서 $N$개의 데이터 포인트를 임의로 추출하여 데이터 집합 $\bf{X_B}$를 만드는데, 이때 한번 추출된 값도 다시 추출 대상으로 고려될 수 있도록 하는 방식을 사용합니다. 즉 어떤 값은 중복될 수도 있고, 아예 포함되지 않을 수도 있습니다. 이 과정을 $L$번 반복하면 원래 데이터 집합의 표본에 해당하는 크기 $N$의 데이터 집합을 $L$개 만들 수 있습니다. 각각의 부트스트랩 데이터 집합에서의 예측치와 실제 매개변수 값과의 차이를 바탕으로 매개변수 추정 값의 통계적 정확도를 판단할 수 있습니다.

베이지안 관점의 장점 중 하나는 사전 지식을 추론 과정에 자연스럽게 포함시킬 수 있다는 점입니다. 예를 들어 멀쩡하게 생긴 동전 하나를 세 번 던졌는데, 세 번 다 앞면이 나왔다고 해봅시다. 고전적인 최대 가능도 추정을 통해 추론한다면 앞으로는 앞면이 나올 확률이 1일 것입니다. 미래의 모든 동전 던지기에서 앞면만 나올 것이라고 예측한다는 말입니다. 대조적으로 베이지안적으로 접근할 경우 적당히 합리적인 사전 확률을 사용한다면 이렇게까지 과도한 결론이 나오지는 않을 것입니다.

빈도적 확률 관점과 베이지안 확률 관점 중 어떤 것이 더 상대적으로 우수한지에 대해서는 끊임없는 논쟁이 있습니다. 베이지안 접근법에 대한 비판 중 하나는 사전 분포가 실제 사전의 믿음을 반영하기보다는 수학적인 편리성을 위해서 선택된다는 것입니다. 베이지안 관점에서는 사전 확률의 선택에 따라 결론이 나기 때문에 추론 과정에 주관이 포함될 수밖에 없습니다. 이 때문에 적절한 사전 확률을 선택하는 것이 어려운 경우도 있습니다. 사전 분포에 대한 의존도를 낮추기 위해 무정보적(noninformative) 사전 분포를 사용하는 경우도 있지만, 이는 서로 다른 모델을 비교하기 어렵게 만듭니다. 그리고 실제로 좋지 않은 사전 분포를 바탕으로 한 베이지안 방법은 부족한 결과물을 높은 확신으로 내놓기도 합니다. 

1.2 확률론 내용이 많아서, 여기서 끊고 1.2.4 가우시안 분포부터 다음 글에서 다루도록 하겠습니다.