헤헤

 

오늘은 cs231n의 lecture 4에 대해서 정리해보겠습니다.

 

딥러닝에서 가장 중요한 개념 중 하나인 backpropagation에 대해서 다루고, neural network가 무엇인지 간단하게 다룹니다.

 

실제로 딥러닝을 코드로 돌리면 backpropagation은 컴퓨터가 모두 계산해주므로 우리가 실제로 직접 backpropagation을 짤 일은 없을 겁니다. 하지만, 가중치를 업데이트하는 가장 핵심 아이디어인 만큼, 제대로 이해할 필요가 있다고 생각합니다.

 

 

 

 

먼저, 새로운 개념인 computational graph에 대해서 얘기해보도록 하겠습니다.

 

computational graph는 어떤 함수를 표현할 때 graph을 이용해서 표현하는 방법입니다.

 

위 슬라이드를 보게 되면, 노드(node)가 존재하고 화살표가 존재하는데 노드는 연산을 의미하고, 화살표는 데이터의 흐름을 나타냅니다.

 

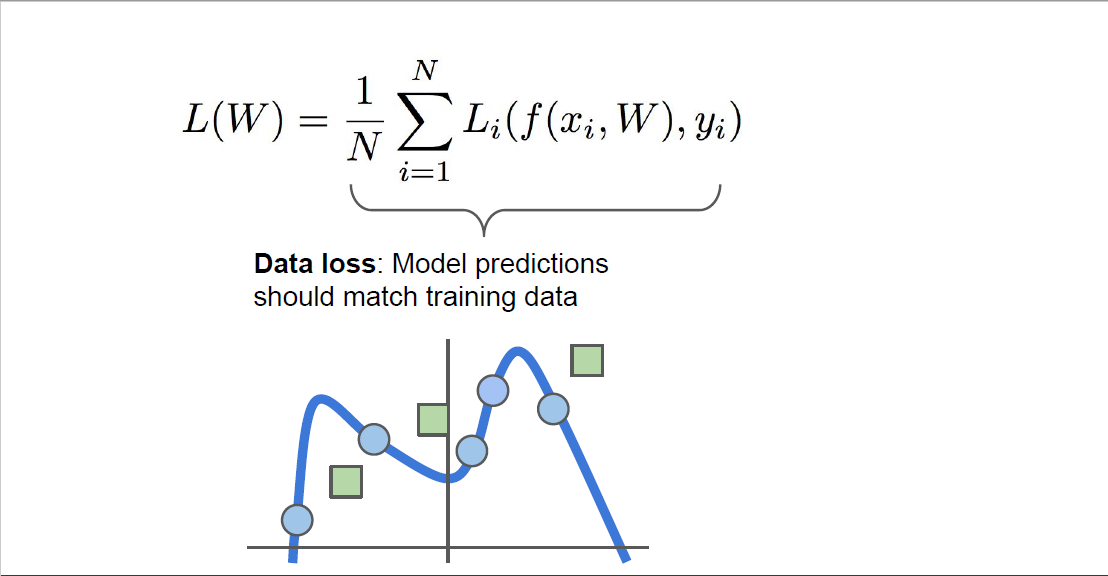
예를 들어서, 위 슬라이드에서 x와 w를 첫 번째 * 노드에 집어넣으면 W*x를 연산해주고, 여기서 나온 값이 $s$(scores)입니다. 그리고 여기에 hinge loss를 계산한 뒤, 여기에 $R(W)$를 더해서 최종 값인 L을 구하게 됩니다.

 

이렇게 computational graph를 이용해서 함수를 표현하게 되면, 모든 변수에 대해서 재귀적으로 gradient를 계산하는 backpropagation을 사용할 수 있게 됩니다.

 

 

 

 

 

 

 

 

 

 

첫 번째로 다뤄볼 예시는 가장 간단한 예시입니다.

 

사용되는 함수는 $f(x, y, z) = (x+y)z$ 라는 함수입니다. 즉, 입력으로 $x$, $y$, $z$를 받아 $(x+y) z$를 출력하는 함수입니다. 이때, $x$ = -2, $y$ = 5, $z$ = -4로 대입해 사용합니다.

 

슬라이드의 오른쪽 부분에는 방금 설명했던 computational graph를 이용하여 함수를 나타냈습니다.

 

computational graph의 위쪽에 녹색으로 표현된 숫자는 변수들의 값과 해당 노드에서의 연산 값을 나타내고 있습니다.

 

우리가 이번 예시에서 해볼 것은, 변수들에 대해서 함수의 gradient를 구해보는 것입니다.

 

 

 

 

 

다음으로는, 중간 노드들을 따로 변수로 지정하였습니다. $q = x + y$이고, $f = qz$입니다.

 

우리가 구하려고 하는 값들은 바로 $\frac {\partial f}{\partial x}$, $\frac {\partial f}{\partial y}$, $\frac{\partial f}{\partial z}$입니다. 

 

각각은 함수의 input 값인 $x$, $y$, $z$가 변했을 때, 함수 $f$에 얼마나 영향을 미치는지를 나타냅니다.

 

 

 

 

 

자 그럼 gradient를 계산해볼까요? 

 

backpropagation의 특징은, 가장 마지막 노드에서 시작해서 input 노드 쪽으로 계산이 된다는 점입니다.

 

따라서 가장 마지막 노드부터 계산을 시작해줍니다.

 

가장 마지막 노드는 함수 $f$ 그 자체를 나타내기 때문에, $\frac {\partial f}{\partial f}$가 되고, 값은 1로 구해집니다.

 

노드마다 아래쪽에 표시되는 빨간색 값은 gradient 값을 나타낸다고 생각하시면 됩니다.

 

 

 

 

다음으로 구해볼 값은 바로 $z$에 대한 gradient입니다.

 

수식으로는 $\frac {\partial f}{\partial z}$로 표현될 수 있으며, 해당하는 값은 파란색 박스 안에 표현되어 있습니다.

 

$f = qz$ 이므로, $f$를 $z$로 편미분 하게 되면 $q$가 되겠죠? 

 

우리가 아까 $q$값을 미리 계산해서 써 두었는데, +로 표기된 노드에서 확인하실 수 있습니다. 값은 3이었죠.

 

따라서 $\frac{\partial f}{\partial z}$의 값은 3이 됩니다.

 

 

 

 

 

 

다음으로는 $q$의 gradient를 구해보겠습니다.

 

수식으로는 $\frac{\partial f}{\partial q}$로 표현될 수 있고, 이에 대한 정답도 파란색 박스에서 찾을 수 있습니다.

 

$f = qz$ 이므로, $f$를 $q$로 편미분 했을 때, 값은 $z$가 되죠. 

 

$z$의 값은 -4라고 했기 때문에, $\frac{\partial f}{\partial q}$의 값은 -4가 됩니다.

 

 

 

 

 

 

 

다음으로는 $y$의 gradient를 구해보겠습니다.

 

어? 근데 $y$는 기존에 구해봤던 $q$나 $z$, $f$와는 차이가 있습니다.

 

바로 함수 $f$의 결괏값에 직접적으로 연결된 변수가 아니라는 점입니다.

 

즉, $y$는 + 연산을 거쳐 $q$를 계산한 뒤, $q$에 * 연산을 거쳐야만 $f$에 도달할 수 있습니다.

 

따라서, $y$의 gradient는 한 번에 구할 수 없으며, 두 번의 걸쳐 구해야 되는 것입니다.

 

여기서 사용되는 방법이 바로 Chain rule인데요, 아마 고등학교 수학을 배우셨다면 미분을 배울 때 많이 보셨겠죠.

 

쉽게 생각하면, gradient는 연산 한번 당 한 step씩 진행된다고 생각하시면 쉽습니다.

 

backpropagation은 끝부터 시작하기 때문에, $f$에서 $y$로 간다고 생각하면 먼저 $q$에서의 gradient를 계산해야 합니다.

 

따라서, 먼저 $\frac {\partial f}{\partial q}$를 계산해줍니다. 이는 아까 -4로 계산했습니다.

 

다음으로는, $\frac {\partial q}{\partial y}$를 계산해줍니다. 이는 빨간색 박스에서 정답을 찾을 수 있습니다. $q = x + y$ 이므로 $q$를 $x$나 $y$로 편미분 하면 1이 됩니다. 따라서 이 값은 1이 됩니다.

 

최종적으로, $\frac {\partial f}{\partial y}$는 -4로 계산됩니다.

 

 

 

 

 

다음으로 구해볼 gradient는 $x$입니다.

 

$x$도 마찬가지로, $f$에 도달하기 위해서 두 번의 연산이 필요합니다.

 

먼저 $f$에서 $q$로 진행되니, $\frac {\partial f}{\partial q}$를 계산해줍니다. 이는 -4로 계산되었습니다.

 

다음으로 $q$에서 $x$로 진행되니, $\frac{\partial q}{\partial x}$를 계산해줍니다. 이는 빨간 박스에서 값을 구할 수 있으며, 값은 1입니다.

 

따라서, 최종적으로 $\frac{\partial f}{\partial x}$는 -4입니다.

 

 

 

 

 

 

앞에서 backpropagation을 실제 예시를 통해서 계산해보았는데요.

 

이번에는 이를 좀 더 일반화해보겠습니다.

 

$x$와 $y$라고 하는 input 값이 존재하고, 이를 input으로 받아 어떤 특정한 연산인 $f$를 진행하며, 결괏값은 $z$로 내게 됩니다. 위에서 다뤘던 예시도 어떻게 보면 이러한 형태를 여러 개 붙여서 만든 케이스라고 볼 수 있습니다.

 

 

 

 

 

 

많은 노드로 구성된 케이스에 대해서 backpropagation을 진행하기 위해서는, local gradient를 계산해야 합니다.

 

 

 

 

 

 

위 슬라이드에 나와있는 gradients란, 함수의 output에 더 가까이 있는 노드에서 넘어오는 gradient를 나타낸 것입니다.

 

 

 

 

 

 

 

 

$\frac{\partial L}{\partial x}$와 $\frac{\partial L}{\partial y}$는  다음과 같이 이전에 넘어온 gradient와 local gradient의 곱으로 나타낼 수 있습니다. 

 

backpropagation의 가장 핵심이 되는 아이디어죠.

 

그렇다면 첫 번째 예시에서 이 내용을 다시 한번 살펴볼까요?

 

 

 

 

위 슬라이드에서 우리가 구하려고 하는 것은 $\frac {\partial f}{\partial x}$ 였습니다.

 

하지만 이를 한 번에 구할 수 없기 때문에, 두 가지 단계를 거쳐서 구해야만 합니다.

 

먼저, "local gradient"를 계산해줍시다.

 

local gradient는 노드에 해당하는 연산을 진행하고 나서 나오는 output에 해당하는 변수를 현재 gradient를 구하려고 하는 변수로 편미분 해주는 것으로 기억해주시면 됩니다.

 

위 슬라이드에서는 local gradient를 구해야 하는 노드가 + 노드 이기 때문에, 이 노드를 진행하고 나서 나오는 output인 $q$를 현재 구하려고 하는 변수인 $x$로 편미분 해주면 됩니다.

 

수식으로 표현하자면 $\frac {\partial q}{\partial x}$가 되는 것이죠. 

 

다음으로는, 이전 단계에서 넘어온 gradients를 확인해야 합니다. 이 경우에는, f에서 q로 gradient가 진행되기 때문에, 이전 단계에서 넘어온 gradients는 $\frac{\partial f}{\partial q}$로 표현할 수 있습니다.

 

최종적으로, $\frac{\partial f}{\partial x}$를 구하기 위해서는, 이전 단계에서 넘어온 gradients인 $\frac{\partial f}{\partial q}$와 local gradient인 $\frac{\partial q}{\partial x}$를 곱하면 되는 것입니다.

 

처음 보시는 분들은 이해가 안 되실 수 있습니다. 저도 이해하는데 꽤 오랜 시간이 걸렸으니까요.

 

앞으로 다른 예시들도 같이 보시면 더 이해가 되지 않을까 싶습니다.

 

 

 

 

 

두 번째로 다뤄볼 예시는 바로 이러한 케이스입니다. 아까보다 훨씬 복잡해졌죠?

 

아까는 더하기와 곱하기 연산만 있었지만, 이번에는 -1을 곱하는 것이나 exp를 취해주는 것도 포함되어 더 다양한 연산들에 대해 gradient를 구해볼 수 있는 케이스가 되었습니다.

 

 

 

 

 

 

 

밑에 4개의 식은 미분 공식을 나타낸 것입니다. 아마 모르는 사람들을 위해서 정리해두신 것 같네요.

 

아까처럼, 맨 마지막부터 연산을 시작합니다. 첫 번째는 $\frac {\partial f}{\partial f}$ 이므로 1입니다.

 

 

 

 

 

다음 다뤄볼 노드는 $x$를 input으로 했을 때, output으로 $\frac {1}{x}$가 나오게 됩니다.

 

따라서, 우리가 구해봐야 하는 것(local gradient)은 output을 input으로 편미분 하는 것이죠.

 

$\frac {1}{x}$를 $x$로 편미분 하면 $-\frac {1}{x^2}$이 됩니다.

 

$x$ 값이 이 지점에서는 1.37이므로, $x$에 1.37을 대입해주면 local gradient를 구할 수 있습니다.

 

거기에다가, 이전에 넘어온 gradient를 곱해줘야 하기 때문에, ($-\frac {1}{1.37^2}$)(1.00) = -0.53이 됩니다.

 

 

 

 

다음 다뤄볼 노드는 input으로 $x$가 들어가고, output으로 $x+1$이 나오게 됩니다.

 

$x+1$을 $x$로 나누면 1이기 때문에, local gradient의 값은 1이 됩니다.

 

이전 노드에서 넘어오는 gradient가 -0.53 이므로, (1)(-0.53) = -0.53이 해당 노드의 gradient가 됩니다.

 

 

 

 

 

다음 노드는 input으로 $x$가 들어가고, output으로 $e^x$가 나오게 됩니다.

 

따라서, $e^x$를 $x$로 편미분 해주면 되고, 편미분 한 결과는 똑같이 $e^x$가 됩니다.

 

해당 노드의 값이 -1이었기 때문에, local gradient는 $e^{-1}$이 되며, 이전에서 넘어오는 gradient인 -0.53과 곱해주면 -0.20로 gradient를 구할 수 있습니다.

 

 

 

똑같은 원리로 풀면 구할 수 있겠죠? 

 

이전과 같이, input은 $x$, output은 $-x$임을 기억하시면 됩니다.

 

 

 

 

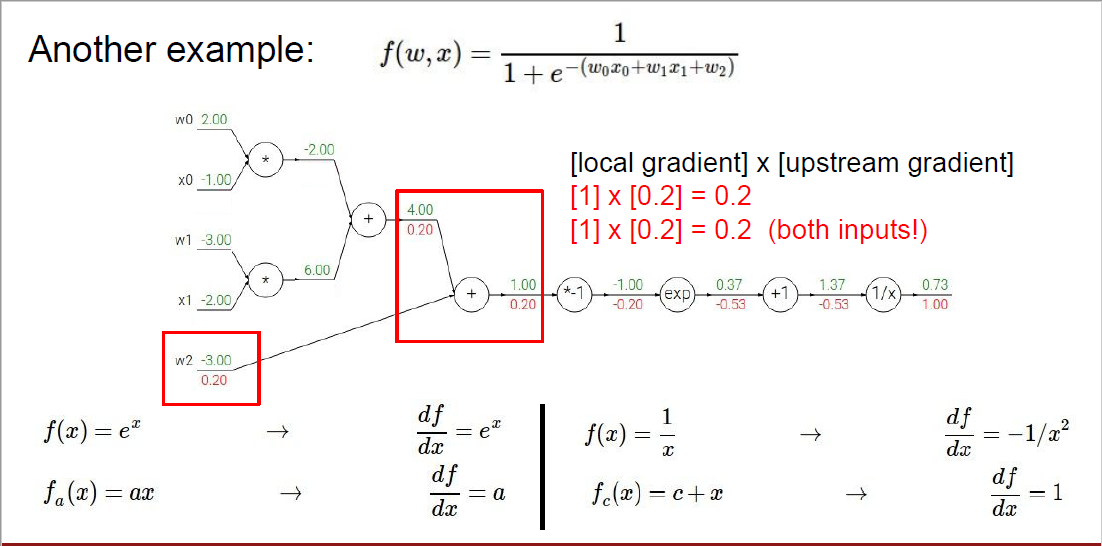
다음으로 구하는 부분은 바로 더하기 연산으로 연결된 부분입니다.

 

$c = a + b$라고 한다면, $c$를 $a$나 $b$로 편미분 했을 때 값은 항상 1이 되겠죠?

 

따라서 더하기 연산으로 연결되어 있는 경우는, local gradient는 항상 1이 됩니다.

 

또 이전 단계에서 넘어오는 gradient가 0.2이므로, 1 x 0.2 = 0.2로 구할 수 있습니다.

 

 

 

 

곱하기 연산이 포함된 부분도 한번 볼까요?

 

먼저 local gradient를 생각해 보겠습니다. 

 

$c = a * b$라고 한다면, $c$를 $a$로 편미분 하면 $b$가 될 것이고 $c$를 $b$로 편미분 하면 $a$가 됩니다. 

 

따라서 $w0$의 local gradient는 $x 0$의 값인 -1이 될 것이고, 이전에 넘어온 gradient가 그림에서 0.2가 되므로, 이를 곱해서 -0.2로 구할 수 있게 됩니다.

 

$x0$도 마찬가지로 local gradient는 $w0$의 값인 2.00이 될 것이고, 이전에 넘어온 gradient가 그림에서 0.2가 되므로, 이를 곱해서 0.4로 구할 수 있게 됩니다.

 

 

 

 

 

다음으로는 노드 하나하나 계산하는 것이 아니라, 여러 개의 노드를 하나의 큰 노드로 바꿀 수 있는 것을 보여주는 예시입니다.

 

강의자가 설명하기로는, 간결하고 간단한 그래프를 그리고 싶은지 아니면 더 디테일하게 그래프를 것인지에 따라 선택할 수 있다고 합니다. 즉 4개의 노드를 다 그릴 것인지, sigmoid 노드 1개로 표현할 것인지 선택의 문제라는 것이죠.

 

$\sigma(x)$를 $\frac{1}{1+e^{-x}}$인 sigmoid function으로 표현할 수 있기 때문에, *-1, exp, +1, 1/x의 4개 노드를 하나의 sigmoid라고 하는 노드로 바꿀 수 있게 됩니다.

 

그렇다면, input으로 $x$가 들어가서 output으로는 sigmoid값이 나오게 되는 것이죠.

 

sigmoid function을 $x$로 편미분 하면 $(1-\sigma(x))(\sigma(x))$가 되는데 현재 $\sigma(x)$의 값이 0.73이므로, (0.73)*(1-0.73) = 0.2로 gradient를 계산할 수 있습니다.

 

 

 

 

backpropagation을 진행할 때, 각 노드에서 나타나는 패턴을 정리해본 것입니다.

 

 

더하기 연산의 경우, 아까 언급했던 것처럼 local gradient가 항상 1이 됩니다. 

 

따라서 이전 gradient의 값을 그대로 가지게 되는데요, 이를 distributor라고 표현했습니다.

 

 

max 연산의 경우, 그림을 참고해보시게 되면 $z$와 $w$ 중에 max를 취한 결과가 바로 $z$죠?

 

gradient를 계산하게 되면, $w$에는 gradient가 0이 되며, $z$에는 2로 계산된 것을 확인할 수 있습니다.

 

max는 여러 값 중에 가장 큰 값만 뽑아내는 연산이기 때문에, gradient를 계산할 때도 뽑아진 가장 큰 값만 gradient를 가지게 됩니다. 

 

만약 max($x$, $y$, $z$) = $z$라면, $z$는 자신의 값을 그대로 output으로 내보내는 것이기 때문에 $z$의 local gradient는 1이 될 것입니다. 나머지 변수들은 애초에 연결된 것이 없기 때문에 local gradient가 0이 되죠.

 

따라서 위 슬라이드의 $z$ gradient의 경우, local gradient가 1이고, 이전에서 넘어오는 gradient 값이 2라서 gradient 값이 2로 계산되는 것을 볼 수 있습니다.

 

 

곱하기 연산의 경우, 아까 언급했던 것처럼 다른 변수의 값이 됩니다.

 

$c = x * y$라고 한다면 $c$를 $x$에 대해서 편미분 했을 때 $y$가 나오게 되겠죠?

 

이를 switcher라고 표현한 것을 볼 수 있습니다.

 

 

 

 

(실제 슬라이드에는 gradient 표기가 따로 되어있지 않아, 슬라이드를 수정하였습니다.)

 

다음으로 다뤄볼 내용은 한 노드가 여러 개의 노드와 연결되어 있는 경우입니다.

 

여러 개의 노드와 연결되면, gradient를 구할 때도 각 노드로부터 오는 gradient를 합쳐서 구하게 됩니다.

 

사실 반대로 생각해보면, $x$를 변화시켰을 때, $q_1$과 $q_2$에 영향을 준다는 사실을 생각해본다면 $x$의 gradient를 계산할 때 $q_1$과 $q_2$로부터 오는 gradient를 합친다는 것이 직관적으로 이해가 되실 겁니다.

 

이전에 gradient를 계산했던 대로, local gradient와 이전 단계에서 넘어오는 gradient를 곱해주는 개념은 그대로 적용되고, 그 대신 여러 branch로부터 gradient가 오는 것을 감안해 더해주는 것만 추가되었다고 보시면 됩니다.

 

 

 

 

 

지금까지는 gradient를 계산할 때, 값이 scalar일 때만 고려했습니다. 하지만 실제 데이터에는 vector 형태를 다뤄야 하죠.

 

따라서 vector 일 때도 다루 어보는 것입니다.

 

차이가 있다면, local gradient가 scalar 값이 아니라 Jacobian matrix라는 점입니다.

 

Jacobian matrix는 z의 각 element를 x의 각 element로 편미분 한 값으로 구성됩니다.

 

간단한 예시를 들자면, 만약 $x$ = [$x_1$, $x_2$, $x_3$] 이고, $z$ = [$z_1$, $z_2$, $z_3$] 라고 한다면

 

Jacobian matrix는 \begin{bmatrix}
\frac{\partial z_1}{\partial x_1} & \frac{\partial z_1}{\partial x_2} & \frac{\partial z_1}{\partial x_3}\\ 
\frac{\partial z_2}{\partial x_1} & \frac{\partial z_2}{\partial x_2} & \frac{\partial z_2}{\partial x_3}\\ 
\frac{\partial z_3}{\partial x_1} & \frac{\partial z_3}{\partial x_2} & \frac{\partial z_3}{\partial x_3}
\end{bmatrix}가 됩니다.

 

 

 

 

 

 

벡터화된 케이스에 대해서 한번 생각해보겠습니다.

 

input vector는 4096차원이고, $max(0, x)$의 연산을 거쳐 4096차원의 output vector를 만들어 냅니다.

 

 

 

 

 

 

따라서 Jacobian matrix의 사이즈는 4096 x 4096이 된다는 사실을 알 수 있습니다.

 

왜냐하면 Jacobian matrix는 output의 각 element를 input의 각 element로 편미분 한 값으로 구성되기 때문이죠.

 

 

 

 

 

실제로 우리가 연산할 때는 minibatch 단위로 진행되기 때문에, Jacobian은 실제로 더 큰 사이즈가 될 것입니다.

 

minibatch를 100으로 지정한다면, 100배 더 큰 matrix가 되겠죠.

 

 

 

 

 

그렇다면 Jacobian Matrix는 어떻게 생겼을까요?

 

input vector의 각 요소들은 output vector의 각 요소에만 영향을 줍니다. ($max(0, x)$ 이므로)

 

따라서 첫 번째 요소는 나머지 요소에 영향을 미치지 않죠. 그렇기 때문에, Jacobian matrix에서 대각선에 해당하는 값만 존재하게 됩니다. (첫 번째 요소는 나머지 2번째 ~ 4096번째 요소에 영향을 미치지 않으므로 Jacobian matrix의 값이 0이 됨)

 

 

 

 

 

 

세 번째로 다뤄볼 예시입니다. 벡터화된 경우에 어떤 식으로 계산되는지 살펴보겠습니다.

 

 

 

 

 

 

$x$와 $W$는 녹색으로 표시된 것처럼 다음과 같이 나타나고, 이들을 곱한 값을 $q$, 그리고 L2 distance를 사용해서 얻은 결괏값은 $f(q)$로 표기할 수 있습니다.

 

계산 자체는 단순하니 행렬 계산에 대한 설명은 생략하도록 하겠습니다.

 

 

 

 

 

 

이전에 했던 것과 마찬가지로 맨 마지막 노드부터 시작합니다. 가장 처음 노드는 항상 1로 시작하는 거 기억하시죠?

 

 

 

 

 

L2 distance의 경우, $q$를 제곱한 것과 동일하기 때문에 이를 $q$로 편미분 해주면 $2q_i$가 됩니다.

 

따라서, $\frac{\partial f}{\partial q}$는 

\begin{bmatrix}
0.44 \\ 
0.52
\end{bmatrix} 로 표현할 수 있습니다.

 

 

 

 

 

언뜻 봤을 때 굉장히 복잡한 식이죠. 하나하나 살펴보겠습니다.

 

이번에 우리가 구해볼 것은 $\frac{\partial q}{\partial W}$인데요. 

 

$\frac{\partial q_k}{\partial W_{i, j}}$ = $1_{k=i}x_j$로 표현되어 있습니다.

 

여기서 $1_{k=i}$는 indicator variable인데요. k와 i가 동일할 때는 1이고 그렇지 않으면 0을 나타냅니다.

 

이게 왜 이런 식으로 나타나는지는 $W \cdot x$를 생각해보시면 이해할 수 있습니다.

 

$q_1$에 해당하는 값은 $W_{11} \times x_1 + W_{12} \times x_2$로 구하게 됩니다. 즉, $k$와 $i$가 같을 때만 $W$의 성분이 $q$에게 영향을 줄 수 있다는 것입니다. 따라서 이렇게 indicator variable이 생겨난 것입니다.

 

 

 

 

 

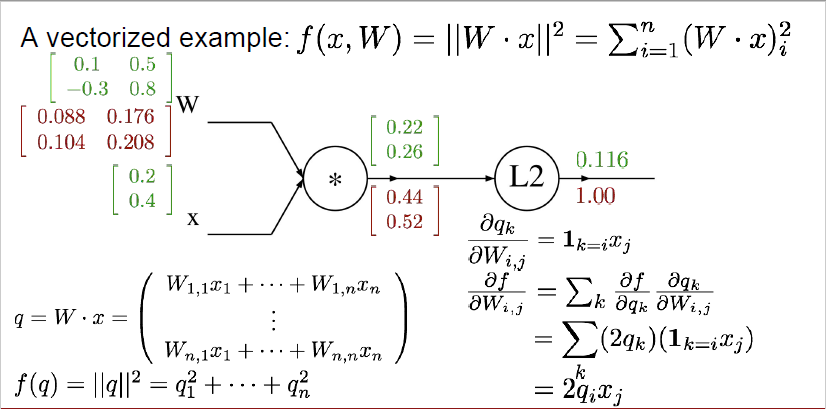
실제 값을 한번 계산해보겠습니다.

 

$\frac{\partial f}{\partial W_{11}}$ = $\frac{\partial f}{\partial q_1}$ $\frac{\partial q_1}{\partial w_{11}}$로 계산될 수 있습니다. 앞 부분은 $2q_1$이 되므로, 0.44가 될 것이며, 뒷부분은 $x_1$가 되므로 0.2가 되어 실제 값은 0.088입니다.

 

$\frac{\partial f}{\partial W_{12}}$ = $\frac{\partial f}{\partial q_1}$ $\frac{\partial q_1}{\partial w_{12}}$로 계산될 수 있습니다. 앞 부분은 $2q_1$이 되므로, 0.44가 될 것이며, 뒷 부분은 $x_2$가 되므로 0.4가 되어 실제 값은 0.176입니다.

 

$\frac{\partial f}{\partial W_{21}}$ = $\frac{\partial f}{\partial q_2}$ $\frac{\partial q_2}{\partial w_{21}}$로 계산될 수 있습니다. 앞 부분은 $2q_2$이 되므로, 0.52가 될 것이며, 뒷 부분은 $x_1$가 되므로 0.2가 되어 실제 값은 0.104입니다. 

 

$\frac{\partial f}{\partial W_{22}}$ = $\frac{\partial f}{\partial q_2}$ $\frac{\partial q_2}{\partial w_{22}}$로 계산될 수 있습니다. 앞 부분은 $2q_2$이 되므로, 0.52가 될 것이며, 뒷 부분은 $x_2$가 되므로 0.4가 되어 실제 값은 0.208입니다.

 

 

 

 

 

$\frac{\partial f}{\partial W}$ 는 vectorized term으로 쓰자면 $2q \cdot x^T$로 표현될 수 있습니다.

 

이는 정답인 $\begin{bmatrix}
0.088 & 0.176\\ 
0.104 & 0.208
\end{bmatrix}$이 되려면 

 

$\begin{bmatrix}
0.44\\ 
0.52
\end{bmatrix}$와 $\begin{bmatrix}
0.2 & 0.4
\end{bmatrix}$를 곱해야 나오기 때문입니다. 

 

그리고 항상 체크해봐야 할 것은 변수의 shape와 gradient의 shape가 항상 같아야 한다는 것입니다. 

 

 

 

 

 

 

다음으로는 $\frac{\partial f}{\partial x}$에 대해서 구해보도록 하겠습니다.

 

x의 local gradient인 $\frac{\partial q_k}{\partial x_i}$는 $W_{k, i}$로 표현되는데요, 이 또한 $q = W \cdot x$를 생각해보면 알 수 있습니다.

 

$W_{11}x_1 + W_{12}x_2 = q_1$이고, $W_{21}x_1 + W_{22}x_2 = q_2$이므로, 

 

$\frac{\partial q_1}{\partial x_1} = W_{11}$가 됩니다.

 

또한, $\frac{\partial q_1}{\partial x_2} = W_{12}$, $\frac{\partial q_2}{\partial x_1} = W_{21}$, $\frac{\partial q_2}{\partial x_2} = W_{22}$이므로 $\frac{\partial q_k}{\partial x_i}$는 $W_{k, i}$가 되는 것을 알 수 있습니다.

 

 

 

 

 

 

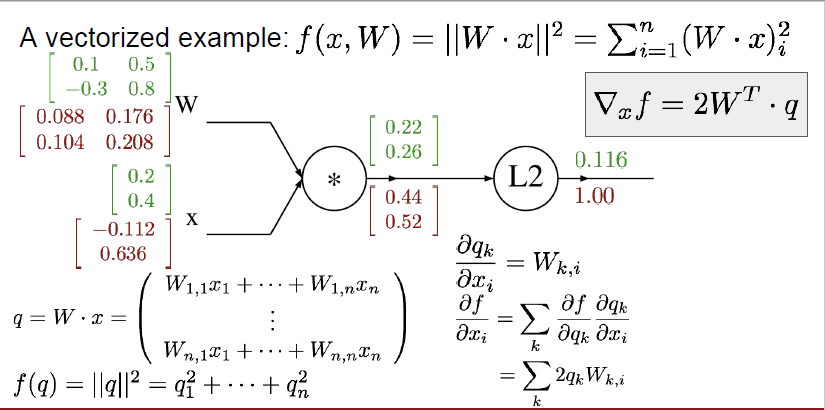
$\frac{\partial f}{\partial x}$를 실제로 구해보자면,

 

$\frac{\partial f}{\partial x_1} = \frac{\partial f}{\partial q_1} \frac{\partial q_1}{\partial x_1} + \frac{\partial f}{\partial q_2} \frac{\partial q_2}{\partial x_1}$가 될 것이며,

 

0.44 * 0.1 + 0.52 * -0.3 = -0.112가 됩니다.

 

$\frac{\partial f}{\partial x_2} = \frac{\partial f}{\partial q_1} \frac{\partial q_1}{\partial x_2} + \frac{\partial f}{\partial q_2} \frac{\partial q_2}{\partial x_2}$가 될 것이며,

 

0.44 * 0.5 + 0.52 * 0.8 = 0.636이 됩니다.

 

이를 vectorized term으로 표현하면, $\frac{\partial f}{\partial x} = 2W^T \cdot q$가 됩니다.

 

 

 

 

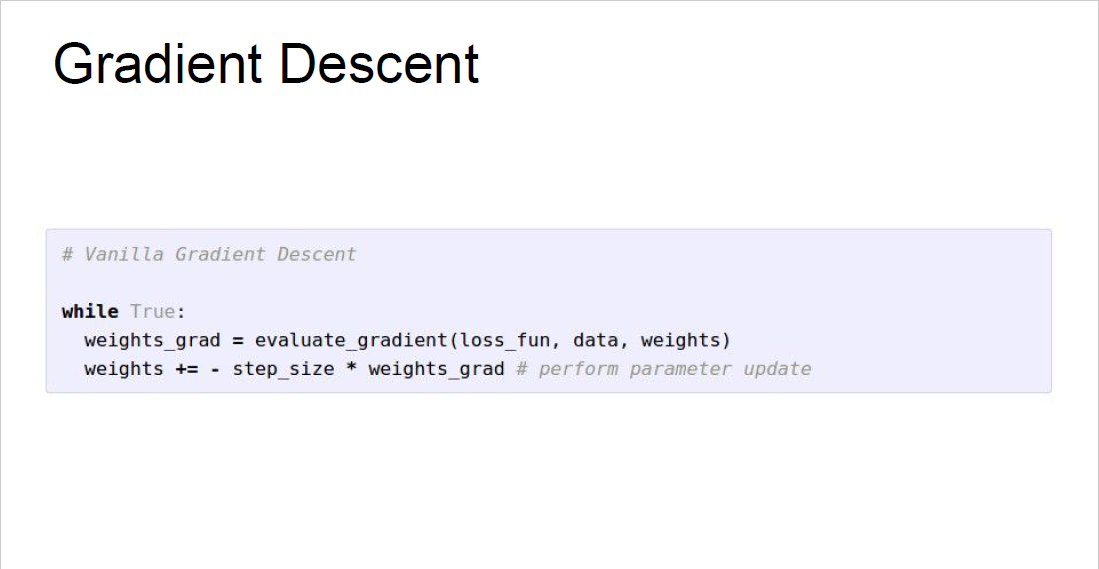
실제 Modularized implementation을 한다고 하면, 다음과 같은 코드로 진행됩니다.

 

먼저 forward pass를 진행합니다. 이를 통해서 각 node의 output을 계산해줍니다.

 

그러고 나서 backward pass를 진행합니다. 이때, 계산하는 node의 순서는 역순으로 진행하게 됩니다.

 

이를 통해서 gradient를 계산합니다.

 

 

 

 

다음과 같이 $x$, $y$를 input으로 받고 $z$를 output으로 할 때 다음과 같은 코드를 만들어볼 수 있습니다.

 

먼저 forward에서는, $x$, $y$를 input으로 받습니다.

 

그리고 이 둘을 곱해서 $z$라는 변수로 저장합니다.

 

Gradient를 계산할 때, $x$, $y$값들이 필요하기 때문에 self.x와 self.y로 저장해줘야 합니다. 

 

그러고 나서 마지막으로는 output인 $z$를 return 해줍니다.

 

backward에서는 dz를 input으로 받는데, 이는 $\frac{\partial L}{\partial z}$를 의미합니다. 즉 이전 단계에서 넘어오는 gradient를 나타낸 것이죠.

 

dx는 self.y * dz로 표현되는데, 이는 x 입장에서 local gradient가($\frac{\partial z}{\partial x}$) y이므로 self.y * dz는 local gradient * 넘어오는 gradient(dz)을 표현한 것입니다.

 

dy도 마찬가지로 이해할 수 있습니다.

 

 

 

여기까지 backpropagation에 대한 설명이었고, 다음으로는 Neural Network에 대해서 정리해보겠습니다.

 

 

 

이전에는 linear score function을 이용하여 score를 얻을 수 있었습니다. 즉, $f = Wx$로 구할 수 있었죠.

 

이제는 layer를 하나 더 쌓아 2-layer Neural Network를 만들어보는 것입니다.

 

3072차원의 x에 $W_1$이라는 matrix를 곱해 100차원의 h를 만들고, 여기에 $max(0, W_1x)$를 취한 뒤, $W_2$라는 matrix를 곱해서 최종 10개 class에 대한 score를 내는 neural network입니다. 

 

강의자가 설명하기를, Neural Network는 class of function으로 함수들을 서로의 끝에 쌓은 것이라고 이해하면 된다고 합니다.

 

 

 

 

 

우리가 처음 lecture 2에서 얘기했던 내용을 기억하시나요?

 

linear classifier에서 사용되는 weight matrix의 각 row가 class를 분류하기 위해 input의 어떤 부분을 살펴봐야 하는지에 대한 정보를 담은 template이라고 얘기했었습니다.

 

하지만, linear classifier에서의 한계점은 이러한 template을 class마다 단 한 개씩만 가질 수 있다는 점이었습니다. 따라서 class 내에서 다양한 형태를 가진다면(예를 들어 왼쪽을 향한 horse가 있고 오른쪽을 향한 horse가 있을 때), 예측력이 크게 감소하게 됩니다. 

 

이러한 단점을 보완할 수 있는 게 바로 Neural Network입니다.

 

그렇다면 이러한 2-layer Neural Network에서는 어떠한 해석을 해볼 수 있을까요?

 

먼저 위 슬라이드의 예시는, 3072차원의 이미지를 input으로 받고, 10개의 class로 분류하는 예시입니다.

 

$x$는 [3072 x 1]의 shape를 가지고 있으며, $W1$은 [100 x 3072]의 shape를 가집니다.

 

이를 통해서 $W1x$ = [100 x 3072] x [3072 x 1] = [100 x 1]의 결과를 나타내겠죠.

 

$W1$에서 현재 100개의 row가 존재하는데, 각각의 row가 바로 template이 됩니다.

 

class의 수가 10개임을 감안하면, class의 수 보다 더 많은 template이 존재한다는 사실을 알 수 있습니다.

 

이를 통해 더 다양한 형태의 template을 학습할 수 있고 같은 class를 나타내는 이미지의 형태가 다르더라도 학습할 수 있게 됩니다.

 

우리가 구한 $W1x$에 $max(0, W1x)$를 적용하여 최종적으로 구한 결과가 바로 $h$가 됩니다.

 

다음으로는 $h$에 $W2$를 곱하게 될 텐데요, $h$는 [100 x 1]의 shape를 가지며 $W2$는 [10 x 100]의 shape를 가집니다.

 

$W2h$ = [10 x 100] x [100 x 1] = [10 x 1]의 결과를 나타내며, 이는 분류해야 하는 class들에 대한 각 class score를 나타냅니다.

 

$W2$를 살펴보자면, 각 class score를 구할 때 $h$의 요소들과의 가중치 합을 하게 됩니다.

 

예를 들면, $w1x1 + w2x2 + w3x3 + ..... w100x100$와 같은 방식이 되는 것이죠.

 

따라서, $W2$의 역할은 다양한 template들에 대해서 가중치 합을 해주는 것입니다. 이를 통해 다양한 templete의 점수들을 반영해서 class score를 더 잘 예측할 수 있게 됩니다.

 

 

 

 

 

실제로 2-layer Neural Network의 학습을 실행시키는데 20줄 정도면 가능하다는 것을 보여주고 있습니다.

 

 

 

 

 

다음으로는, 신경망을 실제 뇌에 있는 뉴런과의 유사함을 통해서 설명해주는 슬라이드입니다.

 

뉴런의 경우, 붙어있는 다른 뉴런으로부터 자극을 받게 되고(dendrite: 수상돌기) 이 자극들을 합쳐줍니다.(cell body) 

 

그러고 나서 cell body로부터 다른 뉴런에게 자극을 보낼지, 아닐지, 혹은 자극의 정도를 더 높이거나 낮출지를 결정해서 자극을 보내는 것으로 결정된다면 axon을 거쳐 다른 뉴런으로 자극을 전달해주는 구조를 가지고 있습니다.

 

오른쪽 아래의 그림을 보게 되면, 우리가 사용하게 되는 신경망의 그림입니다.

 

dendrite를 통해서 다른 뉴런으로부터의 자극을 받아오게 되고, 이를 cell body에서 합칩니다. 

 

실제 신경망에서는 $w_ix_i + b$ 형태로 계산을 하게 되죠.

 

이 값에 대해서 activation function을 거치고, 이 값을 다음 layer로 전달합니다.

 

강의자가 얘기하기로는, 다른 뉴런에게 자극을 보낼지, 아닐지를 결정하는 게 neural network에서의 activation function과 같으며, 실제 뉴런과 가장 비슷한 기능을 수행하는 것은 바로 ReLU라고 합니다.

 

 

 

 

 

하지만, 실제 뉴런 하고는 차이가 많이 존재하기 때문에 이러한 비유를 사용하는 것은 주의해야 한다고 말합니다.

 

 

 

 

 

 

 

 

neural network에서 주요하게 사용되는 activation function은 다음과 같습니다.

 

경험상 Sigmoid, tanh, ReLU 정도를 많이 사용하게 되는 것 같습니다.

 

 

 

 

일반적인 구조는 다음과 같습니다. 

 

input layer에서 hidden layer를 거쳐 output layer로 연산이 진행됩니다.

 

보통 hidden layer와 output layer는 fully-connected layer로 구성됩니다.

 

 

 

 

 

다음과 같은 neural network의 예시를 살펴볼 수 있습니다.

 

activation function은 sigmoid를 사용하고, $x$는 [3x1] 형태로 input vector를 만들어줍니다.

 

hidden layer 1을 h1로 변수를 지정하고, [4x3]의 크기를 가진 $W1$을 이용해서 연산한 뒤, b1을 더해주고 여기에 activation function을 통과시켜 hidden layer 1을 구하게 됩니다.

 

hidden layer 2는 hidden layer 1와 마찬가지로 계산해줍니다.

 

마지막으로 output layer는 하나의 값을 가지므로, [1x4]의 크기를 가진 $W3$를 곱해서 output layer를 계산합니다.

 

 

 

 

 

여기까지 lecture 4의 모든 내용들을 정리해보았습니다.

 

아무래도 슬라이드가 많다 보니, 글이 굉장히 많이 길어졌네요.

 

이번에도 lecture 4를 정리할 수 있는 Quiz를 만들어보았습니다.

 

 

 

cs231n lecture 4 Quiz

 

 

 

Q1.

 

다음 연산에서, 각 노드들의 gradient($\frac{\partial f}{\partial x}$, $\frac{\partial f}{\partial y}$, $\frac{\partial f}{\partial z}$, $\frac{\partial f}{\partial q}$)를 구하세요.

 

 

 

Q2. 

 다음 연산에서 각 노드들의 gradient를 구하세요.

 

 

 

Q3. 

 

다음 연산에서 각 노드들의 gradient를 구하세요.

 

 

Q4. 

 

 

2-layer Neural Network에서 $W1$, $h$, $W2$에 대해서 template matching 관점에서 설명하고, 기존 linear classifier와의 차이점을 설명하세요.

 

 

 

 

 

 

오늘은 lecture 2에 이은, lecture 3에 대해서 정리해보겠습니다.

 

 

이전 시간에 다룬 내용을 정리하는 내용들은 생략하고, 새로운 내용들부터 다뤄보겠습니다.

 

 

 

 

 

저번 시간에는 Linear Classifier에 대해서 알아보았는데요, input data에 곱해지는 weight matrix인 $W$를 어떤 값으로 정하는지에 대해서는 다루지 않았습니다. 따라서 이번 강의에서 그 내용들을 다루게 됩니다.

 

weight matrix의 값을 어떻게 결정하는지에 대한 기준이 바로 loss function인데요. 이는 학습 데이터를 통해서 얻은 weight matrix를 이용해 각 이미지에 대해서 label을 예측하였을 때, 얼마나 못 예측하였는지 정량적으로 알려주는 역할을 합니다. 즉, loss function이 높을수록 예측을 못한 것입니다.

 

우리의 목표는 잘 예측하는 model을 얻는 것이니까... loss function이 낮은 weight matrix를 얻는 것이 목표가 되겠죠? 따라서 loss function을 최소화하는 weight를 효율적으로 찾기 위한 방법인 optimization에 대해서도 다루게 됩니다.

 

 

 

 

 

3개의 학습 예시가 있고, 3개의 class가 있다고 가정해봅시다. 

 

loss function은 현재 classifier가 얼마나 잘하는지를 알려주는 정량적인 척도가 될 것이고요.

 

보통 데이터셋은 ${(x_i, y_i)}$로 표현되고($i$가 하나의 row로 보시면 됩니다.) $i$는 1부터 데이터셋의 크기인 $N$까지 구성됩니다.

 

이때, $x_i$는 image data이고, $y_i$는 integer로 표현된 label입니다. 위 슬라이드 예시의 경우는, label이 0이면 cat, label이 1이면 car, label이 2이면 frog로 정할 수 있겠네요.

 

dataset에 대한 전체 loss는 모든 데이터에 대한 loss의 합을 구한 뒤, dataset의 크기로 나누어 평균을 내서 구하게 됩니다. 여기서 $L_i$가 바로 loss function이 됩니다.

 

 

 

 

 

 

다음으로는 loss function의 구체적인 예시를 다뤄보겠습니다.

 

여기서는 첫 번째로 Multiclass SVM loss를 loss function으로 정했습니다.

 

$s$는 데이터 $x_i$가 입력으로 들어갔을 때, weight matrix인 $W$를 곱해서 얻게 되는 class score를 나타낸 것입니다.

 

SVM loss는 슬라이드에서 나타난 것처럼, 다음과 같이 정의할 수 있는데요.

 

수식을 해석해보자면, $L_i$ : $i$번째 sample에 대한 loss function 값을 의미하고요.

 

if $s_{y_i}$ >= $s_j$+1일 때는 loss function의 값이 0입니다. 여기서 $s_{y_i}$는 정답에 해당하는 class의 class score를 나타내는 것이고, $s_j$는 정답이 아닌 class의 class score를 나타냅니다. 시그마의 아래 부분에 나온 걸 보시면, $j$ $\neq$ $y_i$라고 표기된 것을 볼 수 있는데요, 이는 $j$가 정답이 아닌 class를 나타낸다는 것을 의미합니다.

 

if $s_{y_i}$ < $s_j$+1일 때는 loss function의 값은 $s_j-s_{y_i}+1$로 구할 수 있습니다. 

 

이러한 loss function이 어떠한 의미를 가지고 있는지 한번 생각해볼 필요가 있는데요, if $s_{y_i}$ >= $s_j$+1일 때 loss function이 0이 되는 것을 주목해볼 필요가 있습니다. 

 

만약 정답에 해당하는 class score가 정답이 아닌 class의 class score에다가 1을 더한 값 보다 크거나 같으면 loss function이 0이 됩니다. 즉 정답인 class의 class score는 정답이 아닌 class의 class score보다 1 이상이면 잘 맞춘 것으로 생각한다는 의미입니다. 따라서 Multiclass SVM loss의 특징은 정답인 class의 class score가 정답이 아닌 class의 class score보다 어떤 특정값 이상이기만 하면 잘 맞춘 것으로 생각한다는 것입니다. 여기서 1은 margin이라고 불러주고, 이를 사용하는 사람이 다른 값으로 지정할 수 있는 hyperparameter입니다.

 

 

 

 

Multiclass SVM loss처럼, 0과 어떤 값 중에서 max를 취하는 loss를 Hinge loss라고 부른다고 합니다. Hinge가 한국어로는 경첩인데요, 아마 loss graph가 경첩과 비슷하게 생겨서 붙여진 이름이 아닐까 싶습니다.

 

Hinge Loss를 나타내는 그래프를 살펴보면, x축은 true class의 class score를 나타내고, y축은 loss function의 값을 나타냅니다. true class의 class score가 정답이 아닌 class의 class score보다 1 이상이면 loss가 0을 나타내고 있고, 1 미만이면 선형적으로 loss 값이 증가하고 있는 모습을 나타내고 있습니다. 

 

지금까지 대략 Multiclass SVM loss에 대해서 설명을 드렸는데, 이게 예시가 없으면 사실 헷갈릴 수 있는 부분이라 다음 슬라이드에서 나오게 되는 예시들을 함께 보면서 다시 한번 정리해보겠습니다.

 

 

 

 

 

 

아까 다루었던 SVM loss를 실제 예시를 통해 다시 계산해보겠습니다. 

 

왼쪽의 고양이 사진에 대해서 계산을 해본다고 가정하면, 이 사진의 실제 정답 class는 당연히 cat입니다. 따라서, 정답이 아닌 class(car, frog)의 class score와 정답인 class(cat)의 class score를 비교해서 loss function을 계산해주면 됩니다.

 

먼저 car의 경우, class score가 5.1이고, cat의 class score는 3.2입니다. loss 값의 계산은 $s_j-s_{y_i}+1$로 계산할 수 있으며 계산 값은 2.9가 됩니다. 

 

frog의 경우, cat의 class score가 3.2이고 frog의 class score가 -1.7이므로 cat의 class score가 frog의 class score와 비교했을 때 margin인 1보다 더 큰 상황입니다. 따라서 이때는 loss가 0이 됩니다.

 

 

 

 

 

같은 방식으로, 나머지 두 사진에 대해서도 loss 값을 계산해주게 되면 다음과 같이 구할 수 있습니다.

 

전체 loss는 각 sample들의 loss 값의 합을 sample의 수로 나눠주기 때문에, (2.9 + 0 + 12.9) / 3 = 5.27로 구할 수 있습니다.

 

 

 

 

 

다음 슬라이드는 퀴즈가 포함되어 있습니다. 만약 car score가 약간 바뀌었을 때 loss는 어떻게 변할지 물어보고 있네요.

 

이 문제가 약간 불명확하다고 생각하는데, 왜냐면 car score가 슬라이드에는 3개 있기 때문이죠.

 

강의자에 답변을 토대로 생각해보면, car가 정답인 경우의 class score를 바꾸는 경우를 물어보는 것 같습니다.

 

두 번째 사진의 경우, car의 class score가 4.9로, cat의 class score인 1.3, frog의 class score인 2.0보다 1 이상으로 더 크기 때문에 현재 두 번째 사진은 loss가 0인 상황입니다. 이런 경우, car의 class score를 바꾸더라도 이미 1 이상이므로 loss에는 변화가 없다는 것이 정답이 되겠습니다.

 

 

 

 

다음 질문은 loss의 min과 max가 몇인지를 물어보는 질문입니다.

 

loss의 min은 당연히 0이 되겠고, max는 +$\infty$입니다. 이는 아까 보여준 hinge loss 그래프를 생각해보시면 이해가 될 것 같아요. $s_j$+1보다 클 때는 loss가 0이고, 이보다 작을 때는 선형적으로 올라가는 그래프를 봤었습니다.

 

 

 

 

세 번째 질문은, $W$의 초기값이 작아서 class score가 0에 가깝다면, loss는 어떻게 계산되는지 물어보는 질문입니다.

 

SVM loss의 식을 다시 한번 살펴보도록 할게요. SVM loss는 max(0, $s_j-s_{y_i}+1$) 로 계산할 수 있었는데요.

 

정답인 class의 class score와 정답이 아닌 class의 class score가 0이라면, loss는 1로 계산됩니다.

 

따라서, $L_i$는 class의 수보다 1만큼 작은 값이 될 것입니다. 예를 들어, 위의 예시에서는 class가 3종류 있기 때문에, loss의 값이 2가 되겠죠?(정답인 class에 대해서는 계산을 하지 않기 때문에 1을 빼줍니다.)

 

 

 

 

 

네 번째 질문입니다. 만약 loss 계산을 할 때, 정답인 class의 class score에 대해서도 계산하면 어떻게 되는지 묻고 있습니다.

 

정답인 class에 대해서 계산을 한다면, $s_j$와 $s_{y_i}$가 같다는 것을 의미합니다. 따라서 loss가 1 올라갑니다.

 

 

 

 

다섯 번째 질문입니다. 만약 sum 대신에 mean을 사용하면 어떻게 되는지 묻고 있습니다.

 

사실상 기존 loss 값을 어떤 특정 상수로 나눠주는 것이기 때문에, loss값을 rescale 해주는 효과밖에 되지 않습니다.

 

 

 

 

 

여섯 번째 질문입니다. 만약 기존의 loss function을 제곱으로 바꾸면 어떻게 되는지 묻고 있습니다.

 

기존의 loss function과는 확실히 다른 trick이라고 볼 수 있는데요. 

 

기존의 loss function은 loss 값이 선형적으로 올라갔다면, square term을 이용하면 제곱 형태로 올라가기 때문에 훨씬 더 빠른 속도로 loss값이 올라갑니다.

 

이는 기존 loss function에 비해서 틀렸을 때 훨씬 더 안 좋게 평가하도록 만드는 것입니다.

 

예를 들어, 첫 번째 고양이 사진에 대한 예시를 보면 현재 loss 값이 2.9인데, square term을 이용하면 loss 값이 8.41로 올라갑니다.

 

하지만 세 번째 개구리 사진에 대한 예시를 보면 현재 loss 값이 12.9인데, square term을 이용하면 loss 값이 166.41로 엄청나게 증가함을 알 수 있습니다.

 

따라서 오답에 대해 더 강하게 처벌하는 효과를 가져온다고 볼 수 있습니다.

 

기존의 loss function처럼 선형적으로 증가하는 loss function을 사용할 것인지, 아니면 square term을 사용할 것인지는 설계하는 사람의 선택입니다.

 

 

 

 

 

다음으로는 Multiclass SVM Loss에 대한 예시 코드를 보여주고 있는데요.

 

네 번째 줄에서 margins [y] = 0으로 처리해주는 게 nice trick이라고 소개하고 있습니다.

 

정답인 class에 대해서 loss값을 0으로 지정해버리면 정답인 class만 제외하고 더할 필요 없이 모든 class에 대해서 더하도록 코드를 짤 수 있기 때문입니다.

 

 

 

 

 

만약 우리가 loss 값이 0이 되는 weight matrix인 $W$를 찾았다고 합시다. 그렇다면 $W$는 딱 하나만 존재하는 것일까요?

 

 

 

 

 

 

아닙니다. SVM loss에서는 정답인 class의 class score가 정답이 아닌 class의 class score + 1보다 크거나 같기만 하면 loss를 0으로 계산해주기 때문에, weight matrix에 어떠한 상수를 곱해서 class score를 상수 배 해주어도 동일하게 loss값이 0으로 계산됩니다. 따라서 loss를 0으로 만드는 weight matrix는 여러 개 존재할 수 있습니다.

 

 

 

 

 

 

우리가 이전에 본 예시에서, $W$를 $2W$로 바꾸면 어떻게 될까요?

 

SVM loss에서는 정답인 class의 class score가 정답이 아닌 class의 class score + margin(여기에서는 1) 보다 크거나 같은지 아닌지만 판단하기 때문에 여전히 loss 값은 0으로 유지됩니다.

 

강의를 들을 때, 강의자가 "만약 W를 2배로 올리면, correct score와 incorrect score 사이의 margin 또한 두배가 된다"라고 설명했는데, SVM loss에서의 margin과 단어가 헷갈려서 한참 고민했었습니다. 두 class score 간의 차이 또한 margin이라는 단어로 표현한 것 같은데, 아무래도 SVM loss에서 사용되는 margin과 헷갈릴 수 있기 때문에 difference이나 gap이라고 하는 단어로 설명했다면 더 명확하지 않았을까 하는 아쉬움이 남습니다. (제가 영어권 사람이 아니다 보니 margin, difference, gap 간의 의미상 차이점을 잘 몰라서 이렇게 생각하는 것일 수도 있습니다.)

 

자 그렇다면, 하나의 의문점이 듭니다. $W$도 loss 값이 0이고, $2W$도 loss 값이 0이라면 우리는 어떤 weight를 우리 모델의 parameter로 사용해야 할까요? loss가 0이기만 하면 아무거나 선택해도 되는 것일까요?

 

이러한 고민은 우리가 training data에만 잘 작동하는 weight을 찾으려고 했기 때문에 발생합니다. 저번 시간에 얘기했듯이, machine learning의 목표는 우리가 가지고 있는 training data를 통해 데이터에 있는 정보를 parameter로 요약하고 이를 통해 새로운(본 적 없는) 데이터에 대해서도 잘 예측하는 model을 만드는 것입니다. 즉, training data에 대한 loss가 0인 것은 사실 중요한 것이 아닙니다. 우리가 목표로 하는 것은 test data에 대해서 좋은 성능을 내는 weight를 찾는 것입니다. 

 

test data에 대해서 좋은 성능을 내는 weight를 찾을 수 있도록 loss function에 부가적인 term을 추가해주는데요, 이를 Regularization이라고 합니다.

 

 

 

 

 

우리가 지금까지 얘기한 대로 loss function을 설정하게 되면, training data에 대해서 최대한 잘 분류하는 모델이 만들어지게 됩니다. 슬라이드에 나타난 것처럼, 5개의 점을 분류하는데도 굉장히 복잡한 모델이 만들어진 것을 볼 수 있습니다.

 

 

 

 

 

근데 이렇게 복잡한 모델을 가지고 있게 되면, 녹색 네모처럼 새로운 데이터가 들어왔을 때 적절하게 분류하기가 어렵습니다. 여기서는 따로 용어를 언급하진 않았지만, 이러한 현상을 overfitting(과적합)이라고 부르죠.

 

모델이 training data에 너무 과하게 학습되어 새로운 데이터에 대해서는 성능을 잘 내지 못하는 것을 의미합니다.

 

 

 

 

 

 

 

오히려 파란색의 복잡한 곡선보다는, 녹색처럼 단순한 직선이 데이터들을 더 잘 분류할 수 있습니다. 

 

따라서, model이 너무 복잡해져서 새로운 데이터에 대해 좋은 성능을 내지 못하는 현상을 방지하기 위해 기존의 loss에 Regularization term을 추가하여 model이 더 단순해지도록 만들어줍니다.

 

이는 "가설끼리 경쟁할 때, 가장 단순한 것이 미래의 발견에 대해 일반화하기 쉽다."는 주장인 Occam's Razor에서 영감을 받아 만들어지게 되었습니다.

 

 

 

 

Regularization term은 $\lambda$와 $R(W)$로 구성되어 있는데요, $\lambda$는 regularization을 얼마나 줄 것인지를 나타내는 hyperparameter입니다. 즉, 이 값이 클수록 모델이 더 단순해지도록 강력하게 규제하고, 이 값이 작을수록 모델이 더 단순해지도록 규제하는 것이 적어집니다. 

 

$\lambda$값이 너무 크면, 모델이 너무 단순해져서 새로운 데이터에 대해서 좋은 성능을 내기가 어렵고, 너무 작으면 모델이 너무 복잡해져서 새로운 데이터에 대해서 내기가 어려워집니다. 따라서 적절한 값으로 지정하는 것이 매우 중요하죠.

 

다음으로는 $R(W)$에 대해서 얘기해보려고 합니다. 여기에는 다양한 방법들이 존재할 수 있는데요.

 

먼저 L2 regularization이 있습니다. 이는 모든 weight값들의 제곱 값을 모두 더해서 $R(W)$값으로 지정하게 됩니다. 때로는 미분하는 것을 감안해서 1/2를 곱해주기도 합니다.

 

다음으로는 L1 regularization이 있는데요. 이는 모든 weight값들의 절댓값을 모두 더해서 $R(W)$값으로 지정하게 됩니다. 

 

L1와 L2 regularization을 합해서 만들어지는 Elastic net이라는 것도 있는데요. 여기서는 $\beta$라는 hyperparameter가 추가적으로 들어가게 됩니다. 이 $\beta$는 L2 regularization과 L1 regularization 중에서 어떤 쪽을 더 많이 사용할지 결정하는 hyperparameter가 됩니다. 

 

그 외에도 Max norm regularization, dropout, batch normalization, stochastic depth와 같은 방법들이 존재합니다. 

 

지금까지 공부해오면서 본 바로는 dropout과 batch normalization을 많이 사용되는 것 같네요.

 

Regularization term에 사용되는 방법들은 여러 가지 존재하지만, 결국 기본 아이디어는 model의 복잡성에 규제를 가해서 더 단순한 모델이 될 수 있도록 만드는 것이라는 점을 기억해둬야 합니다.

 

 

 

 

 

 

다음으로는, regularization 방법에 따라서 어떤 weight가 선호되는지를 보여주고 있습니다. 

 

 

$w_1$와 $w_2$ 모두 다 $x$와 내적을 했을 때의 값은 1로 동일합니다. (즉, class score가 같다는 의미겠죠?)

 

L1 regularization을 사용하게 되면, $w_1$의 형태를 더 선호하게 됩니다.

 

보통 영어로는 sparse matrix라고 표현하는데, $w_1$처럼 몇 개만 non-zero 값이고 나머지가 0으로 구성된 경우를 희소 행렬이라고 부르죠. L1 regularization은 이러한 형태를 더 선호합니다.

 

L1 regularization은 weight vector에서 모델의 복잡도를 non-zero의 개수로 측정하게 되고, 이는 0이 아닌 게 많을수록 복잡하다고 판단합니다. 따라서 $w_1$와 같은 형태의 weight vector를 갖도록 강제하죠.

 

 

이와는 다르게, L2 regularization을 사용하게 되면, $w_2$의 형태를 더 선호하게 됩니다.

 

L2 regularization은 weight를 분산시켜 x의 다른 값들에 대해서 영향력을 분산시키는 역할을 합니다.

 

이는 모델이 특정 x에만 치중되어 class score를 계산하는 것이 아니라, x의 여러 요소들을 반영하여 class score를 계산하게 되기 때문에 훨씬 더 강건한(robust) 모델이 되도록 만들어주는 효과를 가져옵니다.

 

 

 

저는 이 부분을 공부하면서 하나의 의문점이 들었는데요. L1과 L2 regularization의 특징을 들어보니 L2가 당연히 좋아 보이는데 L1은 왜 존재하는 것일까? 하는 점이었습니다. 강의자가 분명 이 부분을 몰라서 얘기를 안 한 것은 아니겠지만.... 설명을 해줬어야 하는 부분이라고 생각합니다.

 

 

출처: https://www.quora.com/When-would-you-chose-L1-norm-over-L2-norm

 

 

 

이와 관련되어 다른 분께서 설명해주신 내용을 참고해보자면, L1 regularization은 sparse 한 solution을 만들어내기 때문에, 우리가 input으로 둔 데이터 중에 일부만 가지고 class score를 예측하게 됩니다. 즉, 필요 없는 feature는 제외하는 효과를 가져오는 것이죠. 따라서 feature extraction 혹은 feature selection 효과를 가져오는 것입니다.

 

 

실시간으로 detection을 해야 한다거나 하는 상황처럼, computation을 줄이는 것이 요구되는 상황에서 사용된다고 보시면 될 것 같습니다. 어떻게 보면 L2 regularization과 L1 regularization은 accuracy와 computation 사이의 trade-off라고 생각할 수도 있겠죠?

 

 

 

 

다음으로는 새로운 Classifier와 새로운 loss에 대해서 알아볼 건데요.

 

Multinomial Logistic Regression이라고도 불리는 softmax classifier입니다.

 

우리가 지금까지 구했던 class score를 그대로 쓰지 않고, 새로운 방법을 이용해서 처리해줌으로써 class score에 의미를 부여하려는 시도입니다. 

 

class score를 $s$라고 했을 때, 먼저 각 class score에 exp를 취한 다음, 전체 합으로 나눠줍니다.

 

이를 softmax function이라고 부릅니다. 

 

원하는 class score / 전체 class score의 형태가 되기 때문에, 해당 class가 선택될 확률로 볼 수 있습니다.

 

그렇다면... 이 softmax function을 거친 후의 값이 어떻게 되어야 가장 이상적인 상황이 될까요?

 

정답 class에 해당하는 softmax 값이 1이 되어서 해당 class를 선택될 확률이 1이 되는 것이 가장 좋겠죠?

 

 

 

 

 

 

정답 클래스인 $y_i$가 선택될 확률을 $P(Y = y_i | X = x_i)$이라고 표현한다면, 이것이 최대한 높을수록 좋다고 볼 수 있습니다.

 

따라서 이를 최대화하는 방향으로 weight를 구하면 되는데요, 단순히 이 확률을 높여주는 것보다, log를 취한 값을 최대화하는 것이 수학적으로 더 쉽다고 합니다.

 

그래서 log를 붙여서  $logP(Y = y_i | X = x_i)$로 만들어주고, 이를 최대화하는 방향으로 weight를 조정해줍니다.

 

하지만 loss function은 반대로 나쁨을 측정하는 것이기 때문에, -를 붙여서 계산해줍니다.

 

 

 

loss function 함수의 그래프를 한번 볼까요?

 

$y = -log(x)$ 는 다음과 같은 모양이 되는데요. x값이 1에 가까워질수록 loss가 0에 가까워지고, x값이 1로부터 멀어질수록 loss가 높아지는 모습을 나타냅니다.

 

따라서 이러한 loss function을 사용하게 되면, 정답 class의 class score에 softmax를 취한 값이 1에 가까워질 때 loss 값이 0에 가까워지고 정답 class의 class score에 softmax를 취한 값이 1에서 멀어질수록 loss값이 점점 커집니다. 

 

이러한 형태의 loss function은 자주 사용되니까, 어떤 모양을 가지는 그래프인지는 기억해둘 필요가 있어 보입니다.

 

 

 

 

 

위에서 우리가 했던 예시에 대해서 softmax를 적용한 예시입니다.

 

원래 우리가 구한 class score인 $s$에 exp를 취한 뒤, 이를 전체 합으로 나눠주어 각 class가 선택될 확률을 구하는 모습입니다.

 

 

 

 

 

다음으로는, softmax classifier에 대한 여러 가지 질문들에 대해 고민해보겠습니다.

 

첫 번째, loss $L_i$의 최솟값과 최댓값은 어떻게 될까요?

 

먼저 최솟값을 생각해보겠습니다. 아까 $y = -log(x)$ 그래프를 기억해보시면, 현재 우리가 x 자리에 들어가는 것이 바로 위 슬라이드에서 녹색에 해당하는 probability입니다. 즉 각 class를 선택할 확률이 되죠. 확률은 0보다 크거나 같고 1보다 작거나 같기 때문에, $y = -log(x)$에서 x 값이 0보다 크거나 같고 1보다 작거나 같다는 것입니다.

 

따라서, 해당하는 x의 범위에서 가장 작은 값은 0이 됩니다. 물론, 실제로 loss가 0이 되려면 score 값이 무한대에 가까울 정도로 매우 커야 하므로, 실제로는 0이 될 수는 없고 이론적으로만 가능하다고 합니다.

 

다음으로는 최댓값을 생각해보겠습니다. $y = -log(x)$ 그래프에서, 최댓값은 바로 x가 0일 때에 해당할 것입니다. 

 

근데 softmax를 취한 값이 0이 되려면, exp를 취한 값이 0이 된다는 의미입니다.

 

즉, $e^{-\infty}$ = 0이기 때문에 class score 값이 $-\infty$가 되어야 합니다. 이런 경우도 실제에서는 있기 힘들고, 이론적으로 가능한 값이라고 합니다.

 

 

 

 

다음으로는, $s$ = 0에 가까우면 loss가 어떻게 되는지를 묻고 있습니다.

 

$s$ = 0이면 여기에 exp를 취한 빨간색 네모에 해당하는 값이 전부 1이 될 것입니다. 

 

이 값들에 normalize를 취하면 각 class에 대한 probability가 1 / c가 되겠죠?

 

따라서, loss는 $-log(1/c)$ = $logc$가 됩니다.

 

 

 

 

지금까지 다룬 두 loss function에 대해서 정리해보겠습니다.

 

hinge loss는 정답 class의 class score가 정답이 아닌 class의 class score보다 정해진 margin만큼 크기만 하면 loss 값을 0으로 계산하는 특징이 있습니다.

 

실제 계산하는 식은 $max(0, s_j-s_{y_i}+1)$이였죠.

 

cross-entropy loss 혹은 softmax loss라고 불리는 아래의 loss function은 정답 class가 선택될 확률인 probability가 1로부터 얼마나 멀리 있냐에 따라 loss를 계산해주게 됩니다. 정답 class가 선택될 확률이 1에 가까우면 loss가 0에 가까워지고, 1로부터 멀어지면 loss가 점점 커지는 모습을 보여주게 되죠. 

 

cross-entropy loss를 사용하게 되면 정답 class가 선택될 확률이 1에 가까워지도록, 정답이 아닌 class가 선택될 확률이 0에 가까워지도록 weight를 조절하는 특징을 보입니다.

 

 

 

 

지금까지 다룬 내용들을 정리해봅니다. 

 

우리가 dataset을 가지고 있다면, 각 data point들에 대해서 score function을 통과시켜 class score를 계산하고 이를 이용해서 loss function을 계산해주게 됩니다.

 

우리가 다뤄본 loss function은 Softmax와 SVM loss가 있고요. 앞에서 언급된 Regularization을 이용한다고 하면, 전체 loss 함수는 $L_i + \lambda R(W)$ 형태가 될 것입니다. (위 슬라이드에서는 $\lambda$가 빠져있네요.)

 

다음으로 우리가 생각해볼 것은, 어떻게 최적의 Weight를 찾을 것인가? 하는 문제입니다.

 

이것이 바로 Optimization이라고 하는 영역에 해당합니다.

 

 

 

 

 

강의자가 Optimization을 설명하기 위해서 다음과 같은 예시를 제시하였습니다.

 

우리가 큰 협곡에서 걷고 있다고 가정합니다. 모든 지점에서의 풍경은 parameter $W$ setting에 대응되고요. 

 

즉 위 슬라이드에서 캐릭터가 서있는 저 지점 또한 어떤 특정 parameter 값을 나타낸 것으로 볼 수 있습니다.

 

협곡의 높이는 해당 parameter에 의해서 계산되는 loss와 동일하다고 생각해줍니다.

 

우리의 목표는, 이 협곡의 바닥을 찾기를 바라는 것입니다. (즉 loss가 0인 경우를 찾고 싶다는 얘기죠.)

 

사실 저 그림에서는 단순히 중간 쪽으로 이동해서 협곡의 바닥으로 가면 되는 게 아닌가?라고 생각할 수 있지만, 현실에서는 Weight와 loss function, regularizer들은 큰 차원을 가지고 있고 복잡하기 때문에, 협곡의 바닥에 해당하는 최저점에 곧바로 도달할 수 있는 명시적 해답을 바로 구할 수 없다고 합니다.

 

따라서 현실에서는 다양한 반복적 방법을 사용해서 점점 더 협곡의 낮은 지점으로 나아가는 방식을 통해 협곡의 바닥을 찾아나갑니다.

 

 

 

 

첫 번째로 우리가 생각해볼 수 있는 방법은 바로 random search입니다. 수많은 Weight 중에서 랜덤으로 하나를 샘플링하고, 이를 loss function에 집어넣어서 해당 weight가 얼마나 잘 예측하는지를 보는 것이죠.

 

이런 방식을 이용하면, 정확도가 매우 낮게 나오기 때문에 실제로는 사용할 수 없다고 합니다.

 

 

 

 

 

 

다음으로 생각해볼 수 있는 방법은, slope(기울기)를 따라서 가보는 것입니다.

 

실제로 우리가 계곡에서 걷는다고 생각해보면, 아마 계곡의 바닥으로 가는 경로를 바로 알 수는 없을 겁니다. 하지만 현재 있는 위치에서 어떤 방향으로 가야만 내리막길로 가게 되는지는 바닥의 기울기를 느껴서 찾아낼 수 있습니다. 

 

따라서, 현재 위치에서 어느 방향으로 가야만 내리막인지를 판단한 뒤, 해당 방향으로 약간 이동하고, 또 그 자리에서 다시 방향을 판단한 뒤, 해당 방향으로 약간 이동하고 하는 과정을 계속해서 거쳐서 협곡의 바닥을 찾아나갈 수 있을 것입니다.

 

 

 

 

우리가 고등학교 때 배운 수학에서는 1차원이었기 때문에, 함수의 미분을 이용해서 해당 점의 기울기를 바로 구할 수 있었습니다.

 

하지만 우리가 다루게 되는 문제들은 대부분 고차원의 데이터이기 때문에, 이러한 방식으로 기울기를 구할 수는 없습니다.

 

고차원에서는 gradient라고 하는 개념을 이용하게 되는데요, 이는 다변량 미적분에서 사용되는 개념입니다.

 

gradient는 입력값인 x와 같은 차원을 가지고 있으면서, 각 차원에 대한 편미분 값으로 구성되어 있어서 해당하는 좌표 방향으로 움직였을 때 함수의 기울기가 어떤지 알려줍니다.

 

gradient가 사용되는 이유 중 하나는, gradient의 기하학적인 의미 때문입니다. gradient는 함수가 가장 크게 상승하는 방향을 알려주기 때문에, gradient가 작아지는 방향을 구하게 되면 해당 함수가 가장 빠르게 작아지는 방향을 알 수 있게 됩니다. 

 

gradient에 대해서 궁금하시다면, 구글에서 조금 더 검색해보시면 다양한 자료들을 찾아보실 수 있을 겁니다.

 

한 번쯤은 gradient가 무엇인지에 대해서 공부해보시면 더더욱 좋을 것 같습니다.

 

 

 

 

 

 

Gradient를 실제로 계산하는 방법은 두 가지가 존재하는데, 먼저 첫 번째 방법인 Numeric Gradient를 보도록 하겠습니다.

 

현재 기울기 $W$가 왼쪽 첫 번째 column처럼 구성되어 있다고 한다면, 첫 번째 row에 해당하는 0.34에 매우 작은 양수인 0.0001을 더해줍니다.

 

다음으로 $f(x+h) - f(x) / h$를 계산해서, 해당 weight 값의 $dW$를 계산해주게 됩니다.

 

동일한 방식을 이용해서 weight의 각 값들에 대해서 $dW$를 계산해볼 수 있겠죠?

 

근데 보통 weight의 차원이 매우 크다는 점을 감안하면, 이렇게 계산하는 것은 너무나 느립니다. 왜냐하면 모든 차원의 값들을 전부 계산해야 하기 때문이죠.

 

 

 

 

 

따라서, 사람들은 Loss function을 $W$에 대해서 미분을 하는 방법을 이용해서 Gradient를 계산했습니다.

 

미분을 이용하면, 고차원의 데이터도 한 번에 계산을 할 수 있기 때문이죠.

 

 

 

 

 

요약하자면, Gradient를 계산하는 방법은 Numerical gradient와 Analytic gradient로 총 두 가지 방법이 존재하는데 실제로는 미분을 이용하는 Analytic gradient를 사용합니다.

 

물론 numerical gradient가 필요가 없는 것은 아닙니다. 우리가 짠 코드가 잘 맞는지 확인해보기 위해서 numerical gradient를 이용해 일종의 unit test를 진행하는 데 사용됩니다. 이를 gradient check라고 부른다고 합니다.

 

 

 

 

 

 

실제로 우리가 최적의 $W$를 구하기 위해서는 다음과 같은 방법을 이용해줍니다.

 

먼저 $W$를 랜덤 값으로 초기화해줍니다.

 

그러고 나서, 해당 $W$값을 이용해 loss를 계산해주고, loss function을 $W$로 미분하여 gradient를 계산합니다.

 

gradient가 loss를 가장 빠르게 높여주는 방향을 알려주기 때문에, 이에 -를 취해서 loss를 가장 빠르게 작아지는 방향을 찾습니다. 그리고 해당 방향으로 아주 작은 step 만큼만 이동합니다.

 

이러한 과정을 계속 반복하여, loss가 가장 작은 지점에 수렴하는 방법을 이용합니다.

 

이를 Gradient Descent라고 부릅니다.

 

위 슬라이드에서 step_size라고 하는 변수가 등장하는데, 이는 hyperparameter로 loss가 가장 빠르게 작아지는 방향으로 얼마큼 이동할 것인지 결정합니다. Learning rate라고 하는 용어로도 불립니다. 

 

아마 추후 강의에서 다룰 것이겠지만, step size를 너무 작게 주면, 훨씬 많이 반복해야 loss가 가장 작아지는 지점에 도달하게 되기 때문에 연산하는데 시간이 오래 걸리게 됩니다. 하지만 step size를 너무 크게 주게 되면, 아예 loss function이 발산해버릴 수도 있습니다. 따라서 step size(learning rate)를 얼마로 줄 것인지도 학습에 있어서 중요한 요소가 됩니다.

 

 

 

 

 

그림에서 빨간 부분이 loss가 작은 곳을 나타내고, 파란 부분이 loss가 큰 부분을 나타냅니다.

 

현재 있는 하얀 동그라미의 위치가 original W이며, 여기서 negative gradient 방향으로 이동하는 모습을 그림으로 표현한 것입니다.

 

 

 

 

 

하지만 Gradient Descent 방법을 전체 데이터에 대해서 계산하기에는 연산량이 매우 부담스럽습니다.

 

보통 데이터가 작으면 수천, 수만 개에서 크면 수백만, 수천만 개가 될 수 있습니다.

 

따라서, Gradient를 계산할 때 minibatch라고 하는 일부 데이터만 이용해서 계산해주고 이를 반복해서 계산해 전체 데이터에 대한 Gradient값의 추정치를 계산하는 방법이 바로 SGD라고 볼 수 있습니다.

 

minibatch는 관례적으로 2의 제곱 값을 이용하며 32개, 64개, 128개 등을 주로 사용합니다. 

 

강의자가 얘기하기로는, 이를 stochastic 하다고 이름 붙여진 이유가 바로 해당 방법이 전체 데이터에 대한 gradient값을 Monte Carlo 방식을 이용해서 구하기 때문이라고 합니다.

 

Monte Carlo가 무엇인지에 대해서는 다양한 자료들이 있으니, 찾아보시면 좋을 것 같습니다.

 

Monte Carlo의 대략적인 아이디어는, 수많은 샘플링을 통해서 어떠한 값의 근삿값을 찾아내는 방법론인데요. 현재 SGD가 하고 있는 작업과 사실상 동일합니다. 데이터 중 일부인 minibatch를 이용해서 gradient를 계산하는 작업을 여러 번 반복하여 전체 데이터의 gradient를 근사하는 것이지요.

 

 

 

 

 

Optimization에 이어, 추가적으로 Image Feature와 관련된 내용들을 다루고 있습니다.

 

Deep learning을 사용하기 전에는 Image Feature를 어떻게 추출했는지를 설명하고 있는데요.

 

이미지의 raw pixel을 linear classifier에 넣어주게 되면 multi-modality 등의 문제에 대응할 수 없다는 한계점이 존재했기 때문에, 다음과 같은 two-stage 접근법이 요구되었습니다. 첫 번째로, 이미지의 모습과 관련된 다른 종류의 quantity를 계산하고, 두 번째로 이미지의 feature representation을 얻기 위해 첫 번째에서 구한 것들을 concat 시켰습니다.

 

마지막으로 구해진 feature representation을 linear classifier에 넣어서 이미지들을 분류하곤 했습니다.

 

그렇다면 사람들은 어떻게 이러한 Image Feature를 뽑아야 한다는 아이디어를 생각해냈을까요?

 

 

 

 

왼쪽의 그림을 보시게 되면, 빨간색 data point과 파란색 data point를 linear classifier를 이용해서는 분류할 수 없습니다.

 

하지만, feature transform을 이용해서 data들이 분포된 형태를 바꿔주게 되면, data point들을 linear classifier를 이용해서 분류할 수 있게 됩니다.

 

따라서 사람들은 이미지에 대해서 어떤 feature representation을 뽑아내게 되면, 오른쪽의 모습처럼 data point를 linear classifier를 이용해서 분류할 때 더 좋은 성능을 낼 수 있을 것이라고 생각하게 되었습니다.

 

그렇다면 deep learning이 사용되기 전에 사람들은 어떤 feature representation을 사용했을까요?

 

 

 

 

 

 

첫 번째 예시는 바로 Color Histogram입니다. 

 

색에 대한 스펙트럼을 bucket으로 나누고, 이미지에 존재하는 각 pixel에 대해서 해당 pixel이 어떤 bucket에 해당하는지를 count 합니다.

 

따라서 이를 이용하면, 이미지를 global 하게 봤을 때 어떤 컬러들로 분포되어 있는지를 확인할 수 있습니다.

 

 

 

 

두 번째 예시는 Histogram of Oriented Gradients (HoG)입니다. 

 

사람의 visual system에서 oriented edge가 중요한 역할을 하는데, HoG는 이러한 직관을 포착하려고 시도한 feature representation입니다.

 

강의자가 자세한 방법론을 설명해주진 않았지만, 대략 이미지를 여러 부분으로 localize 해서 각 부분이 어떤 종류의 edge로 구성되어 있는지를 판단해보는 방법이라고 이해해보면 좋을 것 같습니다.

 

슬라이드의 오른쪽 그림을 보면, 왼쪽 원본 그림의 edge를 잘 포착하고 있는 것을 확인할 수 있습니다.

 

자세하게 HoG를 어떻게 구하는지 궁금하시다면, 추가적으로 검색해보시는 것을 추천합니다.

 

 

 

 

 

 

세 번째 예시로는 Bag of Words를 사용하는 방법이 있습니다. 이는 Natural Language Processing에서 영감을 받은 아이디어인데요.

 

예를 들어서, 만약 문단을 표현하고 싶다면 해당 문단에 나타나는 단어들의 빈도를 count 해서 보여줄 수 있겠죠?

 

이러한 아이디어를 이미지에 적용해보는 시도입니다.

 

이미지의 각 patch들을 추출해서, 이를 visual word로 생각하고 k-means clustering 등의 방법을 이용해 군집을 형성해서 "codebook"을 만들어줍니다. 

 

codebook의 각각을 잘 보면, edge와 color를 추출하고 있는 것을 확인할 수 있습니다.

 

다음으로는, 이미지에 대해서 이러한 visual word가 얼마나 자주 나오는지를 count 하여 이미지의 feature representation을 얻을 수 있습니다.

 

 

 

 

 

Deep learning 이전에 사용했던, 5~10년 전에 사용한 Image feature와 현재 ConvNet과의 차이를 비교해보겠습니다.

 

기존에는 이미지에서 BoW나 HoG와 같은 Feature를 추출한 뒤, 이를 f로 표기된 linear classifier에 투입해 각 class에 대한 score를 얻는 방식을 이용하였습니다. Feature는 한 번 추출되면, training 하는 동안 바뀌지 않습니다. 학습이 진행되면 linear classifier만 업데이트되는 방식이었죠.

 

하지만 Deep learning의 경우는 ConvNet을 이용해서 Feature를 추출하게 되고, 학습이 진행될 때 feature를 추출하는 ConvNet도 학습되고, 추출된 feature를 이용해서 각 class의 class score를 예측하는 linear classifier도 학습되게 됩니다.

 

 

 

지금까지 cs231n의 lecture 3에 대해서 정리해보았고, 이번에도 내용을 정리해볼 수 있는 간단한 Quiz를 만들어보았습니다.

 

 

 

cs231n lecture 3 Quiz

 

 

Q1. loss function이 무엇이고, 어떤 의미를 가지고 있나요?

 

Q2. SVM loss와 softmax loss의 차이점은 무엇인가요?

 

Q3. L1 Regularization과 L2 Regularization의 식을 설명하고, 각 Regularization은 어떤 형태의 weight를 선호하는지 이야기해보세요.

 

Q4.

해당 케이스에 대해서 softmax loss를 직접 계산해보세요.

 

Q5. Gradient Descent에 대해서 설명해보고, Gradient Descent과 Stochastic Gradient Descent는 어떤 차이가 있는지 설명해보세요.

 

Q6. Deep learning을 이용해서 이미지 분류를 수행한 경우와, Deep learning을 이용하지 않고 직접 Feature를 추출해서 이미지 분류를 수행한 경우에 어떤 차이가 있는지 설명해보세요.

 

cs231n을 3월 ~ 5월 정도에 걸쳐 한번 정리를 쭉 했으나, 중간중간에 이해를 완벽하게 하지 못하고 넘긴 부분들이 많은 것 같아 학기가 시작하기 전에 다시 한번 싹 정리하는 것을 목표로 하려고 합니다.

 

 

슬라이드를 과도하게 많이 집어넣으면 글 하나당 내용이 너무 많아지는 것을 방지하기 위해서 필요 없다고 생각되는 일부 슬라이드는 제외하면서 작성하려고 합니다.

 

 

또한, lecture를 하나씩 정리할 때마다, 글의 마지막에 해당 lecture를 정리하였다면 바로 대답할 수 있어야 하는 내용들을 Quiz 형식으로 정리해서 만들어보고자 합니다. 이를 통해서 해당 강의의 내용을 내가 잘 이해하고 습득하였는지 확인해보실 수 있을 것이라고 생각합니다. 

 

 

저도 이 분야의 전문가는 아니라서, 어떤 게 가장 중요한지는 명확하지 않아 덜 중요한 내용이 Quiz로 출제될 수 있습니다.

 

 

 

오늘 다룰 내용은 두 번째 강의에 해당하는 Image Classification pipeline에 대해서 정리해보려고 합니다.

 

 

Computer Vision에서, 중요한 task인 Image Classification은 특정한 input image data가 주어졌을 때, 이미 정해져 있는 label 중에서 어떤 label에 해당하는지 구별하는 task입니다. 위에 나온 슬라이드의 경우는, 고양이 사진이 주어졌기 때문에, 고양이라는 label로 구분하는 것이 요구됩니다.

 

 

 

 

인간의 입장에서, 고양이 사진을 보고 고양이로 판단하는 것은 전혀 어렵지 않은 문제입니다. 하지만 컴퓨터가 Image를 분류하는 것은 매우 어려운 일인데, 이는 컴퓨터 입장에서 보는 것이 고양이 사진이 아니라, 거대한 size를 가진 숫자들의 matrix 이기 때문입니다. 슬라이드의 오른쪽에 보이는 것처럼, 실제로 컴퓨터는 0부터 255로 구성되어있는 matrix를 보게 됩니다.

 

이렇게, 컴퓨터가 실제로 보고 있는 pixel 값과, 고양이라고 하는 의미상 아이디어 간에는 큰 gap이 존재하게 되는데, 이를 'Semantic Gap'이라고 설명합니다. 

 

 

 

 

 

 

그렇다면, 컴퓨터가 Image classification을 하면서 어떠한 어려움을 겪게 되는지를 강의에서 설명하고 있습니다.

 

 

첫 번째 어려움은 바로 viewpoint variation입니다. 고양이가 얌전히 있다고 생각하였을 때, 만약 카메라가 움직이게 되면 image data matrix 안에 있는 숫자들은 바뀌지만 고양이라고 하는 label은 그대로 유지됩니다. 따라서 우리가 사용하게 될 알고리즘은 이러한 상황에도 강건하게 작동할 수 있어야 합니다.

 

 

 

 

 

 

 

두 번째로는 밝기와 관련된 어려움으로, 밝은 곳에서 찍었을 때와 어두운 곳에서 찍었을 때 모두 고양이로 분류할 수 있어야 합니다.

 

세 번째로는 자세와 관련된 어려움으로, 가만히 앉아있는 자세뿐 아니라, 누워있거나 다른 자세로 앉아있는 경우에도 고양이로 분류할 수 있어야 합니다.

 

이외에도, 고양이의 신체 중 일부가 가려져 고양이의 일부만 보고도 고양이로 분류할 수 있어야 한다거나, 혹은 고양이의 주변 배경이 고양이와 유사할 때도 고양이로 분류할 수 있어야 합니다.

 

그리고 Intraclass variation이라고 하는 어려움도 존재하는데, 이는 같은 class 여도 그 안에서 차이가 있다는 의미입니다. 즉 고양이들도 모두 똑같이 생긴 것이 아니라, 생김새나 모양, 크기가 다를 수 있는데 이런 경우에도 모두 고양이로 분류할 수 있어야만 합니다.

 

 

 

 

 

숫자로 구성된 list를 분류하는 것과는 다르게, 물체들을 어떻게 인식할지에 대한 명백하고, 직관적인 알고리즘이 존재하지 않습니다. 따라서 image classification은 어려운 문제라고 설명합니다.

 

 

 

 

 

 

그렇다면, 과거 사람들은 이 문제를 그냥 포기했을까요? 그렇지 않습니다. 이 문제를 어떻게든 풀기 위해 다양한 연구들이 진행되어왔습니다. 과거에 사용했던 방법 중 하나는 다음과 같은 방식으로 물체를 분류했습니다. 먼저 사진에서 edge를 찾습니다. (edge는 가장자리라는 뜻으로, 오른쪽의 사진을 보시면 대략 이해할 수 있을 것입니다.) 그러고 나서 모든 코너와 boundary들을 분류하고, 3개의 선이 만나면 코너이고, 귀에는 코너가 몇 개이고... 등등 이런 식으로 어떤 사물을 인식할 수 있는 규칙을 만든 것입니다. 아마 물체마다 가지고 있는 특징들이 있으니, 이런 방법을 통해 해결하려고 한 것 같습니다. 

 

하지만 이러한 방식은 잘 작동하지 않았습니다. 일단 매우 불안정합니다. 방금 설명했지만, 같은 고양이일지라도 포즈가 다르거나, 조명이 다르거나, 혹은 고양이의 일부만 가지고도 고양이를 구별해야 하는데, 이렇게 규칙 기반으로 하게 되면 해당 규칙에서 벗어난 경우는 고양이로 분류할 수 없을 것입니다. 그리고 우리가 구분해야 하는 모든 사물에 대해서 각각 이러한 규칙을 작업해야 한다는 문제점이 있었습니다. 구분해야 하는 사물의 종류가 많다면, 이는 매우 어려운 일이겠죠?

 

이처럼 기존 방법은 세상에 있는 모든 사물들을 분류하기에는 한계점이 명확했기 때문에, 사람들은 세상에 있는 모든 사물들을 분류할 수 있는 어떤 새로운 방법을 찾고 싶어 했습니다.

 

 

 

 

 

그렇게 해서 나오게 된 방법이 바로 Data-Driven Approach입니다. 각 사물에 대해서 규칙을 만드는 것이 아니라, 데이터를 기반으로 학습을 하는 방법을 생각해낸 것입니다.

 

먼저, 이미지와 label로 구성된 dataset을 모은 후, 이를 이용해서 사물을 분류할 수 있는 classifier를 학습시켰습니다. 그러고 나서, 새로운 이미지에 대해서 이 classifier가 사물을 분류하게 됩니다.

 

여기서 classifier가 가지고 있는 의미에 대해서 조금 더 생각해볼 필요가 있는데요, classifier는 다양한 데이터들을 받아들여서 이를 어떤 방법으로 요약하고, 여러 가지 사물들을 어떻게 인식할 것인지에 대한 지식을 요약하는 모델이라고 생각하시면 됩니다. 기존의 방법론은 사람이 직접 손수 각 사물을 어떻게 인식할 것인지에 대한 지식을 규칙을 기반으로 만들어준 것이지만, Data-driven approach에서는 데이터를 기반으로 모델이 이러한 지식을 직접 요약한다는 점에서 차이가 있다고 생각할 수 있습니다.

 

Data-Driven approach에서는 train과 predict 총 두 가지로 모델이 나눠지게 되는데요. train의 경우는 input으로 이미지와 label을 받게 되고, 이 데이터들을 기반으로 여러 가지 사물들을 어떻게 인식할 것인지에 대한 지식을 요약하는 모델이 output으로 나오게 됩니다. classifier라고 하는 용어로 위에서는 소개되었죠.

 

predict는 사물을 분류할 수 있는 model과 분류할 이미지인 test_image를 input으로 받게 되고, model을 이용하여 분류할 이미지인 test_image들의 label을 예측한 결괏값인 test_labels를 output으로 내보내게 됩니다. 즉, Data-Driven approach에서는 '학습'과 '예측'이 분리되어 있음을 나타내고 있습니다.

 

 

 

 

 

첫 번째로 소개할 classifier는 Nearest Neighbor라고 하는 model입니다. 말 그대로, 자신과 가장 가까이에 있는 이웃(데이터)과 같은 label을 가지게 만들어주는 model입니다.

 

train(학습)에서는, 단순히 모든 data와 label들을 기억합니다. 

 

predict(예측)에서는, 예측하려고 하는 이미지의 label을 training image 중에서 가장 유사하다고 생각되는 image의 label로 예측해줍니다.

 

근데 여기서 한 가지 의문이 듭니다. 그렇다면, '가장 유사하다'라는 것을 어떻게 알 수 있을까요? 그것은 곧 다루게 됩니다.

 

 

 

 

 

우리가 사용하는 예시 dataset은 바로 CIFAR10이라고 하는 dataset입니다. 10개의 class로 구성되어있고, 5만 개의 training image로 구성되어 있습니다. 각 class 별로 균등하게 분포되어있어, class 당 5천 개의 image가 있습니다. 그리고 10000개의 testing image도 포함되어 있습니다.

 

 

화면의 오른쪽에는 Test image와 nearest neighbor를 나타내고 있는데요, test image는 label을 예측해야 하는 이미지를 의미하고, nearest neighbor는 해당 이미지와 가장 가깝다고 생각되는 training image들을 나타낸 것입니다. 

 

 

 

 

 

 

 

아까 궁금했던 내용이 드디어 나오게 됩니다. 즉 두 이미지 간의 유사성은 어떻게 판단할 수 있을까요?

 

 

방금 CIFAR10의 예시에서 test image와 training image 간의 유사성은 다음과 같은 척도를 이용해 판단하게 됩니다.

 

 

L1 distance는 두 이미지 간의 차이에 절댓값을 이용해서 계산하게 됩니다. 각 pixel 별로 계산한 뒤에, 모두 합쳐서 하나의 값으로 나타내 줍니다. 즉, 슬라이드에 나온 456이라는 값이 바로 test image와 training image가 얼마나 비슷한지를 나타내는 척도가 되는 것이죠. 이 값이 작으면 작을수록 두 이미지가 비슷하다는 의미가 됩니다.

 

 

 

 

 

다음은 Nearest Neighbor classifier를 코드로 나타낸 것입니다. 먼저 학습하는 코드를 살펴보면, 별도의 연산 과정 없이 image 데이터와 label을 변수로 저장하는 코드를 나타내고 있습니다.

 

 

 

 

 

 

 

다음으로는 예측하는 코드입니다. L1 distance를 이용해서 training dataset에 있는 데이터들과 test image 각각에 대해서 거리를 측정하고, 이것이 가장 작은 것을 label로 지정해주는 코드입니다.

 

 

 

 

 

 

 

강의자료에서는 N개의 data가 있다고 할 때, 학습과 예측이 얼마나 빠른지를 물어보고 있습니다.

 

 

Training은 단순히 자료를 저장하면 되기 때문에, 메모리에 올리는 작업만 하면 되지만, 예측의 경우 N개의 image에 대해서 모두 계산해봐야 하기 때문에, 연산량은 O(N)로 계산됩니다. 이는 문제가 되고, 우리는 예측은 빠르게 하면서 학습은 느려도 되는 상황을 만들고자 합니다. 예측이 빨라야 하는 이유는, 우리가 이러한 예측을 사용하는 것은 핸드폰이나 브라우저, 저전력 device 등에서 사용되기 때문에 연산량이 많이 요구되면 활용하기가 어렵기 때문입니다. 예를 들어, 사진을 찍어서 해당 물체가 어떤 종류의 물체인지 알려주는 앱이 있는데 사진을 찍고 나서 1시간 뒤에 답을 알려준다면 앱으로써의 가치가 없겠죠? 이렇게 생각해보면 예측이 빠른 것이 얼마나 중요한지 알 수 있습니다.

 

 

 

 

 

위의 사진은, 데이터에 대해서 Nearest Neighbor classifier를 적용했을 때 나타나는 모습을 나타낸 것입니다. 빨간색, 파란색, 녹색, 노란색, 보라색은 각각 해당 영역의 label을 나타냅니다. 즉, 이 데이터는 5개의 label을 가진 데이터들로 구성되어 있습니다. 

 

 

이 그림에서 문제가 되는 점은 두 가지 있습니다. 첫 번째로, 사진의 중간쯤에 보이는 yellow island가 형성된다는 점입니다. 이 점은 label을 기준으로는 노란색으로 구별되는 것이 맞지만, 가장 가까이에 있는 점들이 녹색이라는 점에서 녹색으로 분류되었어야 더 자연스러울 것입니다. 두 번째로, 손가락처럼 삐죽삐죽 튀어나오는 부분들이 존재합니다. 그림의 왼쪽에 빨간색과 파란색이 마주하고 있는 영역들을 보면 이러한 현상이 나타나는 것을 알 수 있습니다. 또한, 중심에서 조금 위로 올라가 보면 점은 아무것도 없지만 녹색 영역이 위로 쭉 뻗어있는 영역을 확인할 수 있는데, 이 부분 또한 녹색이 파란색 영역을 침범한 것으로 문제가 될 수 있습니다. 이는 잡음 때문이거나, 결과가 잘못된 것입니다.

 

 

 

 

 

단순히 가장 가까운 이웃에 의해서 label을 결정하는 것이 아니라, 가장 가까운 K개의 데이터들로부터 majority vote를 하는 방식인 K-Nearest Neighbor classifier을 나타내는 슬라이드입니다. 이는 Nearest Neighbor classifier의 일반화된 버전이라고 볼 수 있습니다.

 

 

데이터의 label을 판단하는 데 사용되는 데이터의 개수인 K가 1에서 3, 5로 증가할수록 앞에서 언급된 Nearest Neighbor classifier의 문제점들이 조금 완화되는 모습을 확인할 수 있습니다. K=5 일 때는 손가락처럼 튀어나오는 부분이나, yellow island가 발생하지 않는 모습을 확인할 수 있습니다. 이를 통해, K의 값이 커질수록 잡음에 대해서 더 강건해지면서 decision region이 훨씬 부드러워지는 것을 볼 수 있습니다.

 

 

여기서 하얀색으로 나타난 부분은, KNN에 의해서 label을 결정할 수 없는 부분을 표현한 것입니다.

 

 

 

 

 

KNN을 사용하면서 추가적으로 생각해볼 수 있는 점은, 바로 Distance Metric을 결정하는 것입니다. 이전에는 L1 distance만 소개했으나, 자주 사용되는 distance metric에는 L2 distance도 존재합니다.

 

L2 distance는 두 거리의 차이에 제곱을 취해서 모두 더한 뒤, 다시 제곱근을 취해서 구할 수 있습니다. 보통 중학교, 고등학교 수학에서 두 점 사이의 거리를 구할 때 사용되는 공식과 동일합니다.

 

L1 distance의 경우, 선택하는 좌표계에 의존합니다. 따라서, 좌표계를 바꾸면 점과 점 사이의 L1 distance가 바뀌게 됩니다. 또한, input의 각각이 중요한 의미를 가지고 있다면 L1을 사용하는 것이 좋습니다. 예를 들어서, input data가 4차원이고, 각각 키, 몸무게, 나이, 발 사이즈를 의미한다면, L1을 사용하는 게 좋다는 것입니다.

 

L2 distance의 경우, 좌표계에 의존하지 않습니다. 따라서, 좌표계를 바꾸더라도 점과 점 사이의 L2 distance가 바뀌지 않게 됩니다. L1 distance와 반대로, input이 어떤 것을 의미하는지 모를 때는 L2를 사용하는 것이 좋습니다.

 

이처럼 distance metric을 고르는 것은 공간의 기저에 깔린 기하학에 대한 가정이 달라지기 때문에, 어떤 것을 선택하는지가 중요합니다.

 

 

 

 

위 슬라이드는, distance metric을 어떤 것으로 선택하느냐에 따라 decision region이 달라지는 것을 보여주고 있습니다.

 

L1 distance의 경우, decision region이 좌표계 형태로 나타납니다. 잘 보면 부드러운 느낌보다는, 사각형처럼 나타나는 것을 확인할 수 있습니다.

 

L2 distance의 경우, decision region이 자연스럽게 나타나는 것을 확인할 수 있습니다.

 

 

 

vision.stanford.edu/teaching/cs231n-demos/knn/

 

http://vision.stanford.edu/teaching/cs231n-demos/knn/

 

vision.stanford.edu

이 사이트에서 KNN의 demo을 제공하고 있는데, distance Metric과 K, class 수, 데이터 수를 다르게 지정해보면서 어떤 식으로 영역이 나타나는지를 확인해볼 수 있습니다. 

 

 

 

 

 

K-Nearest neighbor에서 K를 어떻게 결정할지, 혹은 distance metric을 어떤 것을 사용할지는 매우 중요한 부분입니다.

 

하지만, 이는 데이터로부터 학습되는 요소가 아닙니다. 알고리즘을 설계하는 사람이 선택해줘야 하는 값들이죠. 이를 hyperparameter라고 부릅니다. 머신러닝이나 딥러닝에서 매우 매우 자주 사용되는 용어이니, 꼭 기억해두어야 합니다.

 

hyperparameter는 어떤 게 가장 좋은지 바로 알 수 있는 방법이 없기 때문에, 문제에 따라서 다양한 값들을 시도해보고 가장 잘 작동한다고 보이는 값을 이용합니다. 

 

그렇다면, hyperparameter는 단순히 아무 값이나 다 해보면서 선택할까요? 가능한 모든 값을 직접 해보긴 현실적으로 힘들지 않을까요? 따라서 다음으로는 hyperparameter를 어떻게 결정해야 할지에 대해서 얘기해봅니다.

 

 

 

 

첫 번째로 생각해볼 수 있는 방법은 우리의 Dataset에 대해서 가장 잘 작동하는 hyperparameter를 사용해보는 것입니다. 하지만, 이러한 방법은 좋은 방법이 아닙니다. Machine Learning에서는 현재 우리가 가지고 있는 데이터에 대해서 최고 성능을 내는 것이 목표가 아니라, 본 적이 없는 데이터에 대해서 좋은 성능을 내는 것이 목표이기 때문입니다. 따라서, 우리가 가지고 있는 데이터에서만 가장 좋은 성능을 내는 hyperparameter를 사용하는 것은 좋은 선택이라고 보기 어렵습니다. 

 

 

 

 

두 번째로 생각해볼 수 있는 방법은 dataset을 학습용과 테스트용으로 나누고, 테스트 데이터에서 가장 좋은 성능을 내는 hyperparameter를 선택하는 것입니다. 하지만 이 방법도 문제가 있습니다. Test data는 우리가 만든 machine learning model이 본 적 없는 데이터에 대해서 어느 정도 성능을 낼지에 대한 추정치를 주는 역할을 하는데, 이 방법을 이용하면 test data에 대해서 나온 성능이 본 적 없는 데이터를 대표할 수 없게 됩니다. 

 

 

 

 

 

 

세 번째로 생각해볼 수 있는 방법은 데이터를 학습용, 검증용, 테스트용으로 분할시키는 것입니다. 학습용을 이용해서 모델을 학습하고, 검증용에서 가장 좋은 성능을 내는 hyperparameter를 선택한 뒤, 테스트용에서 성능을 점검해보는 것입니다. 이러한 방식을 이용하면 앞에서 나타났던 문제들 모두 발생하지 않게 됩니다. 실제로 대부분 이러한 3 분할 방식을 이용해 모델을 학습시키고, 테스트합니다.

 

 

 

 

 

 

네 번째로 생각해볼 수 있는 방법은 바로 Cross-Validation이라는 방법입니다. 데이터를 크게 학습용과 테스트용으로 나누고, 학습용 데이터를 K개의 fold로 나눈 다음, 한 번씩 돌아가면서 각 fold를 검증용으로 사용하는 것입니다. 이렇게 하면 모델이 훨씬 더 다양한 상황에서 검증을 진행해 더 좋은 hyperparameter를 선택할 수 있게 됩니다. 

 

 

 

 

 

이전에 설명했던 방법인 KNN은 이미지에서 사용하지 않는다고 합니다. 아까 설명했듯이, test time에서는 N개의 데이터 각각에 대해서 거리를 계산하여 가장 가까운 K개의 이미지 중 다수결에 해당하는 label을 지정하기 때문에 연산량이 높아 매우 느립니다. 그리고 픽셀에 대해서 distance metrics을 사용하였을 때, 유용한 정보를 주지 않는다고 합니다.

 

아래 나타난 사진 중 가장 왼쪽은 원본, 그리고 나머지 오른쪽 3개는 원본 이미지에 특수한 처리를 해준 이미지입니다. 하지만, 특수한 처리를 해준 이미지 3개 모두 원본 이미지와의 L2 distance를 계산하였을 때, 같은 값을 가진다고 합니다. 즉, 이러한 거리 척도는 지각적인 유사성에 대응되지 않습니다. (만약 지각적인 유사성에 대응되려면, 거리가 달라야만 합니다.)

 

따라서, 이미지에 대해서는 지각적인 유사성에 대응될 수 있는 다른 거리 척도가 필요합니다.

 

 

 

 

이외에도 차원의 저주라고 하는 문제점이 존재합니다. 

 

KNN이 좋은 성능을 내려면 우리의 training dataset이 공간을 빽빽이 채워야 합니다. 그렇지 않으면 모델이 판단하기에 가장 가까운 이웃이라고 생각하는 데이터가 꽤 멀리 존재할 수 있게 됩니다. (큰 공간에 점들이 듬성듬성 분포되어 있다고 상상해보시면 대략 이해가 가실 것입니다.)

 

문제는, 실제로 training dataset이 공간을 빽빽이 채우는 것은 충분한 학습 데이터가 필요하다는 것을 의미하며 문제의 차원에 지수적입니다. 그림에서 나타난 것처럼, 차원이 하나 늘어날수록 필요한 데이터의 수가 지수적으로 증가함을 알 수 있습니다. 현실적으로는 공간을 빽빽하게 메울 만큼의 데이터를 구하는 것은 불가능합니다. 오히려 데이터를 많이 구할 수 없는 경우들이 많기 때문에 더 적은 데이터로도 학습할 수 있는 모델이나 방법론들이 많이 연구되고 있죠. 

 

 

 

 

 

KNN에 대한 내용을 요약한 것입니다. 앞의 내용을 모두 숙지하셨다면, 읽으면서 아 이런 걸 얘기했었지? 하며 넘어가실 수 있을 겁니다.

 

 

 

다음으로는, Linear Classification에 대해서 다룹니다. 물론 매우 단순한 방법이긴 하지만, 아무리 복잡한 딥러닝 모델이어도 결국에는 가장 기초가 되는 개념은 linear classification이기 때문에 이에 대해서 확실하게 이해하는 것이 중요합니다.

 

 

 

Neural Network(신경망)이라고 하는 것은 결국에 linear classifier들을 여러 개 쌓아서 만든 것입니다. 즉 레고 블록과 같은 것이죠. 

 

 

 

 

 

 

이것이 바로 신경망을 활용한 예시입니다. Input으로는 사진을 넣어주고, output으로는 사진을 설명하는 글을 만들어서 알려줍니다. 사진을 이해하는데 활용되는 것은 CNN이며, 이를 입력으로 받아 글을 만들어주는 것은 RNN 계열의 신경망입니다.

 

 

 

 

 

지금부터 다뤄볼 linear classification은 parameter를 사용하는 모델 중 가장 간단한 모델인데요. 이를 통해 parametric approach에 대해서 알아봅니다.

 

이전에 우리가 사용했던 Nearest Neighbor나 K-Nearest Neighbor의 경우에는 별개의 parameter가 존재할 필요가 없었습니다. Test data를 기준으로 가장 가까운 데이터를 알아내서, 이를 통해 label을 결정하면 되기 때문이었죠. 하지만, Nearest Neighbor의 방식에는 치명적인 문제점이 있었죠. 바로 Test time이 매우 오래 걸린다는 점입니다. 

 

따라서, training time은 오래 걸려도 되지만, test time은 매우 짧을 수 있도록 하는 접근법이 필요한데요. 이것이 바로 parametric approach입니다. Parameter는 training data에 대한 우리의 지식을 요약한 결과라고 보시면 됩니다. 이를 이용하면 test 할 때는 별도의 training data를 이용하지 않고도, parameter만 가지고 본 적 없는 새로운 데이터에 대해서 label을 예측할 수 있게 됩니다. 

 

슬라이드에 나온 구체적인 예시를 한번 볼까요? Input data로는 32x32x3의 이미지 데이터를 받습니다. 총 3072개로 구성된 데이터죠. 이를 f(x, W)라고 하는 함수에 집어넣으면 함수는 주어진 10개의 class에 대해서 class score를 알려줍니다. 여기서 class score란, 해당 class에 속할 가능성을 나타내는 것으로 score가 높을수록 해당 class에 속할 가능성이 높아지게 됩니다.  

 

 

 

 

 

 

앞에서 f(x, W)가 어떤 식으로 구성되어있는지는 얘기해주지 않았는데요. 보통은 다음과 같은 형태로 구성됩니다.

 

W는 가중치를 나타내는 matrix이고, x는 input data, b는 bias를 나타냅니다. Wx + b 연산을 이용하면, 10개의 class score를 얻을 수 있습니다. 

 

우리가 training data를 이용해서 학습을 한다는 것은, 결국 여기서 W를 알아내는 것을 말합니다. 즉, 어떤 이미지 데이터가 입력되었을 때, 10개의 class 중에 어디에 속할지 틀리지 않고 잘 맞출 수 있도록 만들어주는 matrix를 학습하는 것이죠. 

 

여기서 b는 bias를 나타내는데, 이는 데이터를 이용해 학습되지 않으며 보정 효과를 나타냅니다. 예를 들어서, 데이터에 고양이 사진이 개 사진보다 많다면, 고양이에 해당하는 bias가 다른 것보다 더 높은 값을 가지게 될 것입니다. 

 

 

 

 

조금 더 수치적으로 구체적인 예시를 볼까요? 만약 input image가 2x2 짜리 데이터이고, 3개의 class가 존재하는 상황이라고 가정합니다.

 

앞에서 설명한 대로, Wx + b의 연산을 진행하면, 각각의 클래스에 대한 점수를 얻을 수 있게 됩니다. 

 

Cat score를 얻는 과정만 한번 따라가보자면, $W$의 첫 번째 row와 input image를 stretch 한 것과 곱해줍니다.

 

즉 0.2*56 + -0.5*231 + 0.1*24 + 2.0*2 로 계산할 수 있죠. 여기에 bias인 1.1을 더해주면 cat score에 해당하는 -96.8을 얻을 수 있습니다.

 

 

이 슬라이드를 통해 기억해둬야 하는 점은, linear classification을 'template matching'이라고 하는 접근법으로 생각할 수 있다는 점입니다. 즉, 특정한 class를 나타낼 수 있는 template를 학습하는 것이라고 볼 수 있는데요.

 

예를 들어, 위의 슬라이드에서 첫 번째 줄인 [0.2, -0.5, 0.1, 2.0]는 고양이라고 하는 class를 분류할 수 있는 '틀(template)'이라고 보시면 됩니다. 두 번째 줄은 개를 분류하는 틀이 될 것이고, 세 번째 줄은 배를 분류하는 틀이 될 것입니다.

 

여기서 $Wx$는 dot product(내적)을 의미하는데요, 이는 각 클래스에 대한 template과 이미지 pixel 사이의 유사성을 계산한다고 생각할 수 있습니다. 

 

예를 들어서, template이 이미지 pixel과 유사하게 학습되었다면, 내적 값은 높아지게 될 것이고, 결국 해당 class로 분류될 가능성이 높아져 정답을 잘 맞힐 수 있겠죠?

 

 

 

 

 

 

위 슬라이드는, linear classification을 template matching의 관점에서 봤을 때 이를 시각화한 것입니다.

 

아까 weight matrix인 $W$에서 각 행이 각각의 class에 대응되는 template이라는 얘기를 했었는데요, 이를 input image 사이즈와 동일하게 재배열시켜서 만든 것이 바로 아래에 있는 사진들입니다.

 

자세히는 안 보이시겠지만, car의 경우는 우리가 차를 앞쪽에서 바라본 모습이 대략 보이시죠? cat의 경우는 고양이의 두 귀가 사진의 위쪽에 희미하게 보이는 것을 알 수 있고요. horse의 경우도 말의 모습이 어렴풋이 보이는 걸 확인할 수 있습니다. 

 

하지만 이러한 linear classifier에는 한계점이 존재합니다. 각각의 class에 대해서 딱 하나의 template만 학습한다는 것이죠. 따라서 같은 class 내에서도 variation이 존재한다면, 모든 variation들을 평균을 내버립니다. 그렇기 때문에 다양한 케이스에 대해서 모두 학습할 수는 없다는 한계점이 존재합니다.

 

이러한 linear classifier를 레고 블록처럼 여러 개 쌓은 neural network는, 각 class 별로 여러 개의 template을 학습한다고 생각할 수 있으며, 이를 통해 class 내에 존재하는 다양한 variation에 대해서도 학습할 수 있는 힘이 생깁니다. 예를 들어서, 우리가 맨 앞에서 언급했던 대로 고양이의 일부 모습만 보고도 고양이를 구별해야 한다거나, 혹은 고양이의 크기나 생김새가 다를 때도 모두 고양이로 분류하려면 다양한 template을 학습하는 것이 필요할 것입니다.

 

 

 

 

linear classifier를 다른 시각으로도 볼 수 있습니다. 이는 Geometric viewpoint(기하학적 관점)에 해당합니다.

 

이런 관점에서는, image를 고차원 공간에 있는 점으로 인식하게 되며, linear classifier는 한 범주와 다른 범주를 구분 짓는 선형 결정 경계를 만들어냅니다.

 

 

 

 

 

 

다음으로는, linear classifier를 이용해서 구분하기 어려운 케이스들을 보여주고 있습니다.

 

가장 왼쪽의 첫 번째 케이스의 경우는, 1 사분면과 3 사분면이 class 2, 2 사분면과 4 사분면이 class 1에 해당하는 경우인데, 두 class를 완벽하게 구분할 수 있는 linear classifier는 만들 수 없습니다.

 

두 번째 케이스와 세 번째 케이스도 마찬가지입니다. 

 

이렇게, linear classifier로 구분할 수 없는 경우들이 발생하기 때문에, neural network에서는 다양한 non-linearity를 추가해주어 이러한 경우도 분류할 수 있게 만들어줍니다. 

 

 

 

 

지금까지, 각 class의 score를 알려주는 linear score function을 이용했습니다.

 

하지만, 단순히 이 score만 가지고는, 해당 model이 얼마나 이미지를 잘 분류했는지 알 수 있는 방법이 없습니다.

 

잘 분류했는지를 파악해야 이 모델을 당장 쓸 수 있는지, 혹은 더 학습을 진행해서 더 잘 맞출 수 있는 weight을 얻어야 할지 판단할 수 있겠죠?

 

 

 

 

다음 강의에서는, 그렇다면 우리가 구한 weight가 얼마나 좋은지를 알려주는 loss function에 대해서 다루어볼 예정입니다.

 

또한, 임의의 W 값으로부터 시작해서, 최적의 W를 찾기 위해 어떻게 해야 하는지에 대해서도 알아볼 것이고요.

 

ConvNet에 대해서도 알아볼 예정입니다.

 

 

 

 

 

 

지금까지 cs231n의 두 번째 강의인 lecture 2에 대해서 모두 정리해 보았습니다.

 

역시나 혼자 공부할 때와 비교했을 때, 정리하는 글을 작성해보면 훨씬 더 정리가 잘 되는 것 같고 또한 공부한 내용들이 더 잘 정리되는 것 같습니다.

 

이번 Lecture 2를 잘 이해하셨는지 확인해볼 수 있는 문제를 한번 내보도록 하겠습니다.

 

 

 

 

cs231n Lecture 2 Quiz

 

 

 

 

Q1. Semantic Gap이란 무엇인가요?

 

 

Q2. 컴퓨터가 이미지의 class를 분류하는 데 있어서 다양한 어려움들이 존재하는데, 이러한 어려움들의 예시를 제시하세요.

 

 

Q3. Data-Driven approach는 왜 나오게 되었으며, 어떤 process를 가지고 있나요?

 

 

Q4. K-Nearest Neighbor classifier는 어떤 방식으로 test data의 label을 결정하나요? 또 K의 값이 커질수록 어떠한 특징을 나타내나요?

 

 

Q5. KNN에서 사용된 distance metric이 두 가지 있습니다. 각각의 식과, 특징은 무엇인가요?

 

 

Q6. Hyperparameter란 무엇인지 정의를 설명하고, 어떤 방법을 통해 hyperparameter를 결정하나요?

 

 

Q7. linear classifier는 template matching의 아이디어로도 설명할 수 있는데요. template matching이란 무엇인가요?

 

 

Q8. 데이터가 총 8개의 차원으로 구성되어있고, 우리가 분류해야 하는 class가 10개라고 했을 때, $Wx + b$에서 $W$, $x$, $b$ 각각의 차원은 어떻게 되어야 하나요? 그리고 $W$를 template의 관점에서 어떻게 해석할 수 있는지 설명하세요.

 

 

Q9. linear classifier의 한계점이 두 가지 있었습니다. 두 가지 한계점에 대해서 설명하세요.