cs231n - lecture 3: Loss Functions and Optimization

 

 

오늘은 lecture 2에 이은, lecture 3에 대해서 정리해보겠습니다.

 

 

이전 시간에 다룬 내용을 정리하는 내용들은 생략하고, 새로운 내용들부터 다뤄보겠습니다.

 

 

 

 

 

저번 시간에는 Linear Classifier에 대해서 알아보았는데요, input data에 곱해지는 weight matrix인 $W$를 어떤 값으로 정하는지에 대해서는 다루지 않았습니다. 따라서 이번 강의에서 그 내용들을 다루게 됩니다.

 

weight matrix의 값을 어떻게 결정하는지에 대한 기준이 바로 loss function인데요. 이는 학습 데이터를 통해서 얻은 weight matrix를 이용해 각 이미지에 대해서 label을 예측하였을 때, 얼마나 못 예측하였는지 정량적으로 알려주는 역할을 합니다. 즉, loss function이 높을수록 예측을 못한 것입니다.

 

우리의 목표는 잘 예측하는 model을 얻는 것이니까... loss function이 낮은 weight matrix를 얻는 것이 목표가 되겠죠? 따라서 loss function을 최소화하는 weight를 효율적으로 찾기 위한 방법인 optimization에 대해서도 다루게 됩니다.

 

 

 

 

 

3개의 학습 예시가 있고, 3개의 class가 있다고 가정해봅시다. 

 

loss function은 현재 classifier가 얼마나 잘하는지를 알려주는 정량적인 척도가 될 것이고요.

 

보통 데이터셋은 ${(x_i, y_i)}$로 표현되고($i$가 하나의 row로 보시면 됩니다.) $i$는 1부터 데이터셋의 크기인 $N$까지 구성됩니다.

 

이때, $x_i$는 image data이고, $y_i$는 integer로 표현된 label입니다. 위 슬라이드 예시의 경우는, label이 0이면 cat, label이 1이면 car, label이 2이면 frog로 정할 수 있겠네요.

 

dataset에 대한 전체 loss는 모든 데이터에 대한 loss의 합을 구한 뒤, dataset의 크기로 나누어 평균을 내서 구하게 됩니다. 여기서 $L_i$가 바로 loss function이 됩니다.

 

 

 

 

 

 

다음으로는 loss function의 구체적인 예시를 다뤄보겠습니다.

 

여기서는 첫 번째로 Multiclass SVM loss를 loss function으로 정했습니다.

 

$s$는 데이터 $x_i$가 입력으로 들어갔을 때, weight matrix인 $W$를 곱해서 얻게 되는 class score를 나타낸 것입니다.

 

SVM loss는 슬라이드에서 나타난 것처럼, 다음과 같이 정의할 수 있는데요.

 

수식을 해석해보자면, $L_i$ : $i$번째 sample에 대한 loss function 값을 의미하고요.

 

if $s_{y_i}$ >= $s_j$+1일 때는 loss function의 값이 0입니다. 여기서 $s_{y_i}$는 정답에 해당하는 class의 class score를 나타내는 것이고, $s_j$는 정답이 아닌 class의 class score를 나타냅니다. 시그마의 아래 부분에 나온 걸 보시면, $j$ $\neq$ $y_i$라고 표기된 것을 볼 수 있는데요, 이는 $j$가 정답이 아닌 class를 나타낸다는 것을 의미합니다.

 

if $s_{y_i}$ < $s_j$+1일 때는 loss function의 값은 $s_j-s_{y_i}+1$로 구할 수 있습니다. 

 

이러한 loss function이 어떠한 의미를 가지고 있는지 한번 생각해볼 필요가 있는데요, if $s_{y_i}$ >= $s_j$+1일 때 loss function이 0이 되는 것을 주목해볼 필요가 있습니다. 

 

만약 정답에 해당하는 class score가 정답이 아닌 class의 class score에다가 1을 더한 값 보다 크거나 같으면 loss function이 0이 됩니다. 즉 정답인 class의 class score는 정답이 아닌 class의 class score보다 1 이상이면 잘 맞춘 것으로 생각한다는 의미입니다. 따라서 Multiclass SVM loss의 특징은 정답인 class의 class score가 정답이 아닌 class의 class score보다 어떤 특정값 이상이기만 하면 잘 맞춘 것으로 생각한다는 것입니다. 여기서 1은 margin이라고 불러주고, 이를 사용하는 사람이 다른 값으로 지정할 수 있는 hyperparameter입니다.

 

 

 

 

Multiclass SVM loss처럼, 0과 어떤 값 중에서 max를 취하는 loss를 Hinge loss라고 부른다고 합니다. Hinge가 한국어로는 경첩인데요, 아마 loss graph가 경첩과 비슷하게 생겨서 붙여진 이름이 아닐까 싶습니다.

 

Hinge Loss를 나타내는 그래프를 살펴보면, x축은 true class의 class score를 나타내고, y축은 loss function의 값을 나타냅니다. true class의 class score가 정답이 아닌 class의 class score보다 1 이상이면 loss가 0을 나타내고 있고, 1 미만이면 선형적으로 loss 값이 증가하고 있는 모습을 나타내고 있습니다. 

 

지금까지 대략 Multiclass SVM loss에 대해서 설명을 드렸는데, 이게 예시가 없으면 사실 헷갈릴 수 있는 부분이라 다음 슬라이드에서 나오게 되는 예시들을 함께 보면서 다시 한번 정리해보겠습니다.

 

 

 

 

 

 

아까 다루었던 SVM loss를 실제 예시를 통해 다시 계산해보겠습니다. 

 

왼쪽의 고양이 사진에 대해서 계산을 해본다고 가정하면, 이 사진의 실제 정답 class는 당연히 cat입니다. 따라서, 정답이 아닌 class(car, frog)의 class score와 정답인 class(cat)의 class score를 비교해서 loss function을 계산해주면 됩니다.

 

먼저 car의 경우, class score가 5.1이고, cat의 class score는 3.2입니다. loss 값의 계산은 $s_j-s_{y_i}+1$로 계산할 수 있으며 계산 값은 2.9가 됩니다. 

 

frog의 경우, cat의 class score가 3.2이고 frog의 class score가 -1.7이므로 cat의 class score가 frog의 class score와 비교했을 때 margin인 1보다 더 큰 상황입니다. 따라서 이때는 loss가 0이 됩니다.

 

 

 

 

 

같은 방식으로, 나머지 두 사진에 대해서도 loss 값을 계산해주게 되면 다음과 같이 구할 수 있습니다.

 

전체 loss는 각 sample들의 loss 값의 합을 sample의 수로 나눠주기 때문에, (2.9 + 0 + 12.9) / 3 = 5.27로 구할 수 있습니다.

 

 

 

 

 

다음 슬라이드는 퀴즈가 포함되어 있습니다. 만약 car score가 약간 바뀌었을 때 loss는 어떻게 변할지 물어보고 있네요.

 

이 문제가 약간 불명확하다고 생각하는데, 왜냐면 car score가 슬라이드에는 3개 있기 때문이죠.

 

강의자에 답변을 토대로 생각해보면, car가 정답인 경우의 class score를 바꾸는 경우를 물어보는 것 같습니다.

 

두 번째 사진의 경우, car의 class score가 4.9로, cat의 class score인 1.3, frog의 class score인 2.0보다 1 이상으로 더 크기 때문에 현재 두 번째 사진은 loss가 0인 상황입니다. 이런 경우, car의 class score를 바꾸더라도 이미 1 이상이므로 loss에는 변화가 없다는 것이 정답이 되겠습니다.

 

 

 

 

다음 질문은 loss의 min과 max가 몇인지를 물어보는 질문입니다.

 

loss의 min은 당연히 0이 되겠고, max는 +$\infty$입니다. 이는 아까 보여준 hinge loss 그래프를 생각해보시면 이해가 될 것 같아요. $s_j$+1보다 클 때는 loss가 0이고, 이보다 작을 때는 선형적으로 올라가는 그래프를 봤었습니다.

 

 

 

 

세 번째 질문은, $W$의 초기값이 작아서 class score가 0에 가깝다면, loss는 어떻게 계산되는지 물어보는 질문입니다.

 

SVM loss의 식을 다시 한번 살펴보도록 할게요. SVM loss는 max(0, $s_j-s_{y_i}+1$) 로 계산할 수 있었는데요.

 

정답인 class의 class score와 정답이 아닌 class의 class score가 0이라면, loss는 1로 계산됩니다.

 

따라서, $L_i$는 class의 수보다 1만큼 작은 값이 될 것입니다. 예를 들어, 위의 예시에서는 class가 3종류 있기 때문에, loss의 값이 2가 되겠죠?(정답인 class에 대해서는 계산을 하지 않기 때문에 1을 빼줍니다.)

 

 

 

 

 

네 번째 질문입니다. 만약 loss 계산을 할 때, 정답인 class의 class score에 대해서도 계산하면 어떻게 되는지 묻고 있습니다.

 

정답인 class에 대해서 계산을 한다면, $s_j$와 $s_{y_i}$가 같다는 것을 의미합니다. 따라서 loss가 1 올라갑니다.

 

 

 

 

다섯 번째 질문입니다. 만약 sum 대신에 mean을 사용하면 어떻게 되는지 묻고 있습니다.

 

사실상 기존 loss 값을 어떤 특정 상수로 나눠주는 것이기 때문에, loss값을 rescale 해주는 효과밖에 되지 않습니다.

 

 

 

 

 

여섯 번째 질문입니다. 만약 기존의 loss function을 제곱으로 바꾸면 어떻게 되는지 묻고 있습니다.

 

기존의 loss function과는 확실히 다른 trick이라고 볼 수 있는데요. 

 

기존의 loss function은 loss 값이 선형적으로 올라갔다면, square term을 이용하면 제곱 형태로 올라가기 때문에 훨씬 더 빠른 속도로 loss값이 올라갑니다.

 

이는 기존 loss function에 비해서 틀렸을 때 훨씬 더 안 좋게 평가하도록 만드는 것입니다.

 

예를 들어, 첫 번째 고양이 사진에 대한 예시를 보면 현재 loss 값이 2.9인데, square term을 이용하면 loss 값이 8.41로 올라갑니다.

 

하지만 세 번째 개구리 사진에 대한 예시를 보면 현재 loss 값이 12.9인데, square term을 이용하면 loss 값이 166.41로 엄청나게 증가함을 알 수 있습니다.

 

따라서 오답에 대해 더 강하게 처벌하는 효과를 가져온다고 볼 수 있습니다.

 

기존의 loss function처럼 선형적으로 증가하는 loss function을 사용할 것인지, 아니면 square term을 사용할 것인지는 설계하는 사람의 선택입니다.

 

 

 

 

 

다음으로는 Multiclass SVM Loss에 대한 예시 코드를 보여주고 있는데요.

 

네 번째 줄에서 margins [y] = 0으로 처리해주는 게 nice trick이라고 소개하고 있습니다.

 

정답인 class에 대해서 loss값을 0으로 지정해버리면 정답인 class만 제외하고 더할 필요 없이 모든 class에 대해서 더하도록 코드를 짤 수 있기 때문입니다.

 

 

 

 

 

만약 우리가 loss 값이 0이 되는 weight matrix인 $W$를 찾았다고 합시다. 그렇다면 $W$는 딱 하나만 존재하는 것일까요?

 

 

 

 

 

 

아닙니다. SVM loss에서는 정답인 class의 class score가 정답이 아닌 class의 class score + 1보다 크거나 같기만 하면 loss를 0으로 계산해주기 때문에, weight matrix에 어떠한 상수를 곱해서 class score를 상수 배 해주어도 동일하게 loss값이 0으로 계산됩니다. 따라서 loss를 0으로 만드는 weight matrix는 여러 개 존재할 수 있습니다.

 

 

 

 

 

 

우리가 이전에 본 예시에서, $W$를 $2W$로 바꾸면 어떻게 될까요?

 

SVM loss에서는 정답인 class의 class score가 정답이 아닌 class의 class score + margin(여기에서는 1) 보다 크거나 같은지 아닌지만 판단하기 때문에 여전히 loss 값은 0으로 유지됩니다.

 

강의를 들을 때, 강의자가 "만약 W를 2배로 올리면, correct score와 incorrect score 사이의 margin 또한 두배가 된다"라고 설명했는데, SVM loss에서의 margin과 단어가 헷갈려서 한참 고민했었습니다. 두 class score 간의 차이 또한 margin이라는 단어로 표현한 것 같은데, 아무래도 SVM loss에서 사용되는 margin과 헷갈릴 수 있기 때문에 difference이나 gap이라고 하는 단어로 설명했다면 더 명확하지 않았을까 하는 아쉬움이 남습니다. (제가 영어권 사람이 아니다 보니 margin, difference, gap 간의 의미상 차이점을 잘 몰라서 이렇게 생각하는 것일 수도 있습니다.)

 

자 그렇다면, 하나의 의문점이 듭니다. $W$도 loss 값이 0이고, $2W$도 loss 값이 0이라면 우리는 어떤 weight를 우리 모델의 parameter로 사용해야 할까요? loss가 0이기만 하면 아무거나 선택해도 되는 것일까요?

 

이러한 고민은 우리가 training data에만 잘 작동하는 weight을 찾으려고 했기 때문에 발생합니다. 저번 시간에 얘기했듯이, machine learning의 목표는 우리가 가지고 있는 training data를 통해 데이터에 있는 정보를 parameter로 요약하고 이를 통해 새로운(본 적 없는) 데이터에 대해서도 잘 예측하는 model을 만드는 것입니다. 즉, training data에 대한 loss가 0인 것은 사실 중요한 것이 아닙니다. 우리가 목표로 하는 것은 test data에 대해서 좋은 성능을 내는 weight를 찾는 것입니다. 

 

test data에 대해서 좋은 성능을 내는 weight를 찾을 수 있도록 loss function에 부가적인 term을 추가해주는데요, 이를 Regularization이라고 합니다.

 

 

 

 

 

우리가 지금까지 얘기한 대로 loss function을 설정하게 되면, training data에 대해서 최대한 잘 분류하는 모델이 만들어지게 됩니다. 슬라이드에 나타난 것처럼, 5개의 점을 분류하는데도 굉장히 복잡한 모델이 만들어진 것을 볼 수 있습니다.

 

 

 

 

 

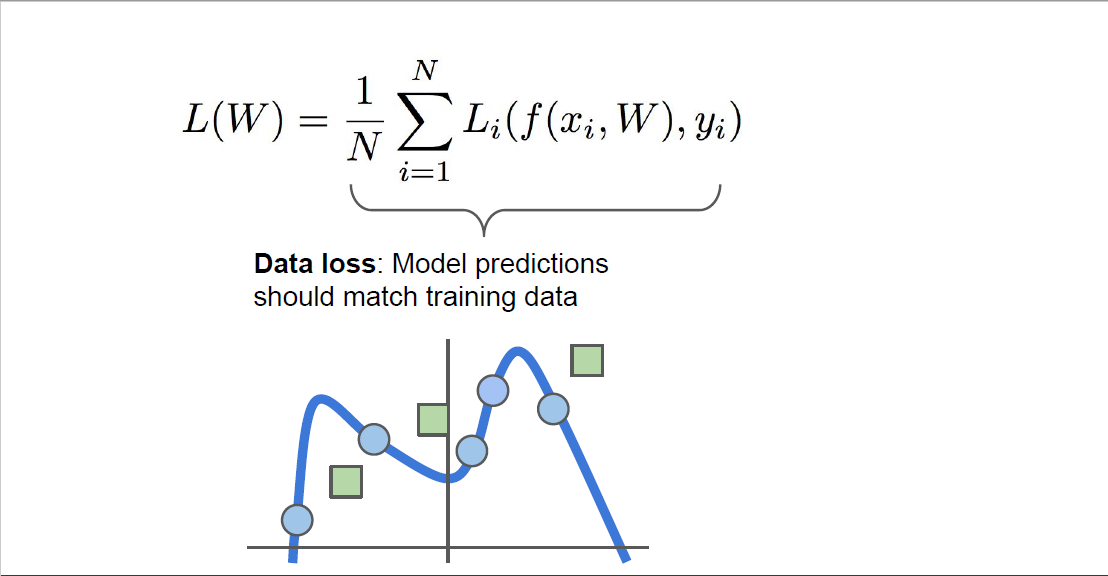
근데 이렇게 복잡한 모델을 가지고 있게 되면, 녹색 네모처럼 새로운 데이터가 들어왔을 때 적절하게 분류하기가 어렵습니다. 여기서는 따로 용어를 언급하진 않았지만, 이러한 현상을 overfitting(과적합)이라고 부르죠.

 

모델이 training data에 너무 과하게 학습되어 새로운 데이터에 대해서는 성능을 잘 내지 못하는 것을 의미합니다.

 

 

 

 

 

 

 

오히려 파란색의 복잡한 곡선보다는, 녹색처럼 단순한 직선이 데이터들을 더 잘 분류할 수 있습니다. 

 

따라서, model이 너무 복잡해져서 새로운 데이터에 대해 좋은 성능을 내지 못하는 현상을 방지하기 위해 기존의 loss에 Regularization term을 추가하여 model이 더 단순해지도록 만들어줍니다.

 

이는 "가설끼리 경쟁할 때, 가장 단순한 것이 미래의 발견에 대해 일반화하기 쉽다."는 주장인 Occam's Razor에서 영감을 받아 만들어지게 되었습니다.

 

 

 

 

Regularization term은 $\lambda$와 $R(W)$로 구성되어 있는데요, $\lambda$는 regularization을 얼마나 줄 것인지를 나타내는 hyperparameter입니다. 즉, 이 값이 클수록 모델이 더 단순해지도록 강력하게 규제하고, 이 값이 작을수록 모델이 더 단순해지도록 규제하는 것이 적어집니다. 

 

$\lambda$값이 너무 크면, 모델이 너무 단순해져서 새로운 데이터에 대해서 좋은 성능을 내기가 어렵고, 너무 작으면 모델이 너무 복잡해져서 새로운 데이터에 대해서 내기가 어려워집니다. 따라서 적절한 값으로 지정하는 것이 매우 중요하죠.

 

다음으로는 $R(W)$에 대해서 얘기해보려고 합니다. 여기에는 다양한 방법들이 존재할 수 있는데요.

 

먼저 L2 regularization이 있습니다. 이는 모든 weight값들의 제곱 값을 모두 더해서 $R(W)$값으로 지정하게 됩니다. 때로는 미분하는 것을 감안해서 1/2를 곱해주기도 합니다.

 

다음으로는 L1 regularization이 있는데요. 이는 모든 weight값들의 절댓값을 모두 더해서 $R(W)$값으로 지정하게 됩니다. 

 

L1와 L2 regularization을 합해서 만들어지는 Elastic net이라는 것도 있는데요. 여기서는 $\beta$라는 hyperparameter가 추가적으로 들어가게 됩니다. 이 $\beta$는 L2 regularization과 L1 regularization 중에서 어떤 쪽을 더 많이 사용할지 결정하는 hyperparameter가 됩니다. 

 

그 외에도 Max norm regularization, dropout, batch normalization, stochastic depth와 같은 방법들이 존재합니다. 

 

지금까지 공부해오면서 본 바로는 dropout과 batch normalization을 많이 사용되는 것 같네요.

 

Regularization term에 사용되는 방법들은 여러 가지 존재하지만, 결국 기본 아이디어는 model의 복잡성에 규제를 가해서 더 단순한 모델이 될 수 있도록 만드는 것이라는 점을 기억해둬야 합니다.

 

 

 

 

 

 

다음으로는, regularization 방법에 따라서 어떤 weight가 선호되는지를 보여주고 있습니다. 

 

 

$w_1$와 $w_2$ 모두 다 $x$와 내적을 했을 때의 값은 1로 동일합니다. (즉, class score가 같다는 의미겠죠?)

 

L1 regularization을 사용하게 되면, $w_1$의 형태를 더 선호하게 됩니다.

 

보통 영어로는 sparse matrix라고 표현하는데, $w_1$처럼 몇 개만 non-zero 값이고 나머지가 0으로 구성된 경우를 희소 행렬이라고 부르죠. L1 regularization은 이러한 형태를 더 선호합니다.

 

L1 regularization은 weight vector에서 모델의 복잡도를 non-zero의 개수로 측정하게 되고, 이는 0이 아닌 게 많을수록 복잡하다고 판단합니다. 따라서 $w_1$와 같은 형태의 weight vector를 갖도록 강제하죠.

 

 

이와는 다르게, L2 regularization을 사용하게 되면, $w_2$의 형태를 더 선호하게 됩니다.

 

L2 regularization은 weight를 분산시켜 x의 다른 값들에 대해서 영향력을 분산시키는 역할을 합니다.

 

이는 모델이 특정 x에만 치중되어 class score를 계산하는 것이 아니라, x의 여러 요소들을 반영하여 class score를 계산하게 되기 때문에 훨씬 더 강건한(robust) 모델이 되도록 만들어주는 효과를 가져옵니다.

 

 

 

저는 이 부분을 공부하면서 하나의 의문점이 들었는데요. L1과 L2 regularization의 특징을 들어보니 L2가 당연히 좋아 보이는데 L1은 왜 존재하는 것일까? 하는 점이었습니다. 강의자가 분명 이 부분을 몰라서 얘기를 안 한 것은 아니겠지만.... 설명을 해줬어야 하는 부분이라고 생각합니다.

 

 

출처: https://www.quora.com/When-would-you-chose-L1-norm-over-L2-norm

 

 

 

이와 관련되어 다른 분께서 설명해주신 내용을 참고해보자면, L1 regularization은 sparse 한 solution을 만들어내기 때문에, 우리가 input으로 둔 데이터 중에 일부만 가지고 class score를 예측하게 됩니다. 즉, 필요 없는 feature는 제외하는 효과를 가져오는 것이죠. 따라서 feature extraction 혹은 feature selection 효과를 가져오는 것입니다.

 

 

실시간으로 detection을 해야 한다거나 하는 상황처럼, computation을 줄이는 것이 요구되는 상황에서 사용된다고 보시면 될 것 같습니다. 어떻게 보면 L2 regularization과 L1 regularization은 accuracy와 computation 사이의 trade-off라고 생각할 수도 있겠죠?

 

 

 

 

다음으로는 새로운 Classifier와 새로운 loss에 대해서 알아볼 건데요.

 

Multinomial Logistic Regression이라고도 불리는 softmax classifier입니다.

 

우리가 지금까지 구했던 class score를 그대로 쓰지 않고, 새로운 방법을 이용해서 처리해줌으로써 class score에 의미를 부여하려는 시도입니다. 

 

class score를 $s$라고 했을 때, 먼저 각 class score에 exp를 취한 다음, 전체 합으로 나눠줍니다.

 

이를 softmax function이라고 부릅니다. 

 

원하는 class score / 전체 class score의 형태가 되기 때문에, 해당 class가 선택될 확률로 볼 수 있습니다.

 

그렇다면... 이 softmax function을 거친 후의 값이 어떻게 되어야 가장 이상적인 상황이 될까요?

 

정답 class에 해당하는 softmax 값이 1이 되어서 해당 class를 선택될 확률이 1이 되는 것이 가장 좋겠죠?

 

 

 

 

 

 

정답 클래스인 $y_i$가 선택될 확률을 $P(Y = y_i | X = x_i)$이라고 표현한다면, 이것이 최대한 높을수록 좋다고 볼 수 있습니다.

 

따라서 이를 최대화하는 방향으로 weight를 구하면 되는데요, 단순히 이 확률을 높여주는 것보다, log를 취한 값을 최대화하는 것이 수학적으로 더 쉽다고 합니다.

 

그래서 log를 붙여서  $logP(Y = y_i | X = x_i)$로 만들어주고, 이를 최대화하는 방향으로 weight를 조정해줍니다.

 

하지만 loss function은 반대로 나쁨을 측정하는 것이기 때문에, -를 붙여서 계산해줍니다.

 

 

 

loss function 함수의 그래프를 한번 볼까요?

 

$y = -log(x)$ 는 다음과 같은 모양이 되는데요. x값이 1에 가까워질수록 loss가 0에 가까워지고, x값이 1로부터 멀어질수록 loss가 높아지는 모습을 나타냅니다.

 

따라서 이러한 loss function을 사용하게 되면, 정답 class의 class score에 softmax를 취한 값이 1에 가까워질 때 loss 값이 0에 가까워지고 정답 class의 class score에 softmax를 취한 값이 1에서 멀어질수록 loss값이 점점 커집니다. 

 

이러한 형태의 loss function은 자주 사용되니까, 어떤 모양을 가지는 그래프인지는 기억해둘 필요가 있어 보입니다.

 

 

 

 

 

위에서 우리가 했던 예시에 대해서 softmax를 적용한 예시입니다.

 

원래 우리가 구한 class score인 $s$에 exp를 취한 뒤, 이를 전체 합으로 나눠주어 각 class가 선택될 확률을 구하는 모습입니다.

 

 

 

 

 

다음으로는, softmax classifier에 대한 여러 가지 질문들에 대해 고민해보겠습니다.

 

첫 번째, loss $L_i$의 최솟값과 최댓값은 어떻게 될까요?

 

먼저 최솟값을 생각해보겠습니다. 아까 $y = -log(x)$ 그래프를 기억해보시면, 현재 우리가 x 자리에 들어가는 것이 바로 위 슬라이드에서 녹색에 해당하는 probability입니다. 즉 각 class를 선택할 확률이 되죠. 확률은 0보다 크거나 같고 1보다 작거나 같기 때문에, $y = -log(x)$에서 x 값이 0보다 크거나 같고 1보다 작거나 같다는 것입니다.

 

따라서, 해당하는 x의 범위에서 가장 작은 값은 0이 됩니다. 물론, 실제로 loss가 0이 되려면 score 값이 무한대에 가까울 정도로 매우 커야 하므로, 실제로는 0이 될 수는 없고 이론적으로만 가능하다고 합니다.

 

다음으로는 최댓값을 생각해보겠습니다. $y = -log(x)$ 그래프에서, 최댓값은 바로 x가 0일 때에 해당할 것입니다. 

 

근데 softmax를 취한 값이 0이 되려면, exp를 취한 값이 0이 된다는 의미입니다.

 

즉, $e^{-\infty}$ = 0이기 때문에 class score 값이 $-\infty$가 되어야 합니다. 이런 경우도 실제에서는 있기 힘들고, 이론적으로 가능한 값이라고 합니다.

 

 

 

 

다음으로는, $s$ = 0에 가까우면 loss가 어떻게 되는지를 묻고 있습니다.

 

$s$ = 0이면 여기에 exp를 취한 빨간색 네모에 해당하는 값이 전부 1이 될 것입니다. 

 

이 값들에 normalize를 취하면 각 class에 대한 probability가 1 / c가 되겠죠?

 

따라서, loss는 $-log(1/c)$ = $logc$가 됩니다.

 

 

 

 

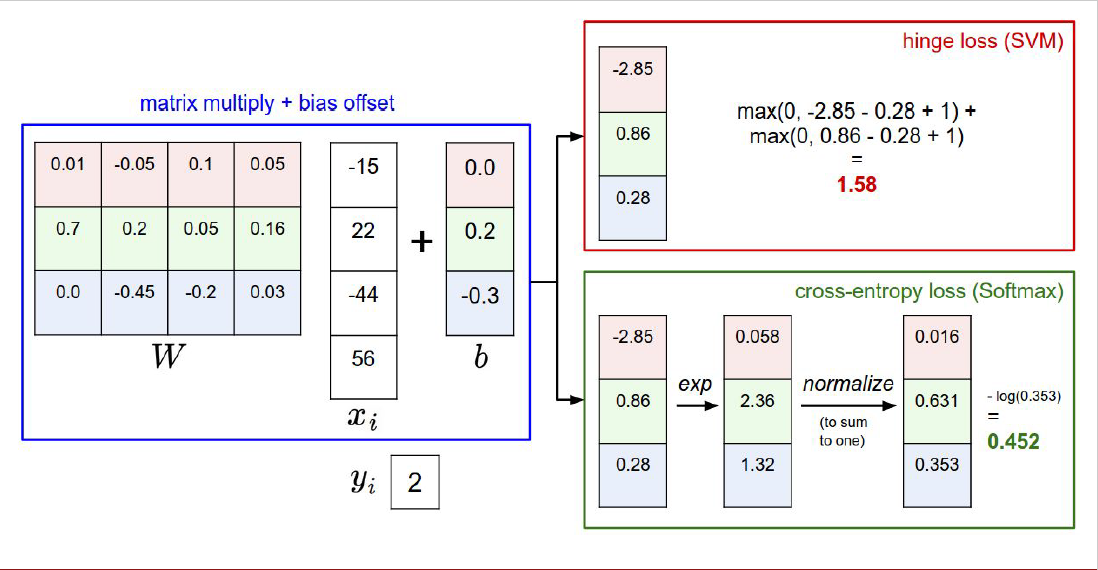
지금까지 다룬 두 loss function에 대해서 정리해보겠습니다.

 

hinge loss는 정답 class의 class score가 정답이 아닌 class의 class score보다 정해진 margin만큼 크기만 하면 loss 값을 0으로 계산하는 특징이 있습니다.

 

실제 계산하는 식은 $max(0, s_j-s_{y_i}+1)$이였죠.

 

cross-entropy loss 혹은 softmax loss라고 불리는 아래의 loss function은 정답 class가 선택될 확률인 probability가 1로부터 얼마나 멀리 있냐에 따라 loss를 계산해주게 됩니다. 정답 class가 선택될 확률이 1에 가까우면 loss가 0에 가까워지고, 1로부터 멀어지면 loss가 점점 커지는 모습을 보여주게 되죠. 

 

cross-entropy loss를 사용하게 되면 정답 class가 선택될 확률이 1에 가까워지도록, 정답이 아닌 class가 선택될 확률이 0에 가까워지도록 weight를 조절하는 특징을 보입니다.

 

 

 

 

지금까지 다룬 내용들을 정리해봅니다. 

 

우리가 dataset을 가지고 있다면, 각 data point들에 대해서 score function을 통과시켜 class score를 계산하고 이를 이용해서 loss function을 계산해주게 됩니다.

 

우리가 다뤄본 loss function은 Softmax와 SVM loss가 있고요. 앞에서 언급된 Regularization을 이용한다고 하면, 전체 loss 함수는 $L_i + \lambda R(W)$ 형태가 될 것입니다. (위 슬라이드에서는 $\lambda$가 빠져있네요.)

 

다음으로 우리가 생각해볼 것은, 어떻게 최적의 Weight를 찾을 것인가? 하는 문제입니다.

 

이것이 바로 Optimization이라고 하는 영역에 해당합니다.

 

 

 

 

 

강의자가 Optimization을 설명하기 위해서 다음과 같은 예시를 제시하였습니다.

 

우리가 큰 협곡에서 걷고 있다고 가정합니다. 모든 지점에서의 풍경은 parameter $W$ setting에 대응되고요. 

 

즉 위 슬라이드에서 캐릭터가 서있는 저 지점 또한 어떤 특정 parameter 값을 나타낸 것으로 볼 수 있습니다.

 

협곡의 높이는 해당 parameter에 의해서 계산되는 loss와 동일하다고 생각해줍니다.

 

우리의 목표는, 이 협곡의 바닥을 찾기를 바라는 것입니다. (즉 loss가 0인 경우를 찾고 싶다는 얘기죠.)

 

사실 저 그림에서는 단순히 중간 쪽으로 이동해서 협곡의 바닥으로 가면 되는 게 아닌가?라고 생각할 수 있지만, 현실에서는 Weight와 loss function, regularizer들은 큰 차원을 가지고 있고 복잡하기 때문에, 협곡의 바닥에 해당하는 최저점에 곧바로 도달할 수 있는 명시적 해답을 바로 구할 수 없다고 합니다.

 

따라서 현실에서는 다양한 반복적 방법을 사용해서 점점 더 협곡의 낮은 지점으로 나아가는 방식을 통해 협곡의 바닥을 찾아나갑니다.

 

 

 

 

첫 번째로 우리가 생각해볼 수 있는 방법은 바로 random search입니다. 수많은 Weight 중에서 랜덤으로 하나를 샘플링하고, 이를 loss function에 집어넣어서 해당 weight가 얼마나 잘 예측하는지를 보는 것이죠.

 

이런 방식을 이용하면, 정확도가 매우 낮게 나오기 때문에 실제로는 사용할 수 없다고 합니다.

 

 

 

 

 

 

다음으로 생각해볼 수 있는 방법은, slope(기울기)를 따라서 가보는 것입니다.

 

실제로 우리가 계곡에서 걷는다고 생각해보면, 아마 계곡의 바닥으로 가는 경로를 바로 알 수는 없을 겁니다. 하지만 현재 있는 위치에서 어떤 방향으로 가야만 내리막길로 가게 되는지는 바닥의 기울기를 느껴서 찾아낼 수 있습니다. 

 

따라서, 현재 위치에서 어느 방향으로 가야만 내리막인지를 판단한 뒤, 해당 방향으로 약간 이동하고, 또 그 자리에서 다시 방향을 판단한 뒤, 해당 방향으로 약간 이동하고 하는 과정을 계속해서 거쳐서 협곡의 바닥을 찾아나갈 수 있을 것입니다.

 

 

 

 

우리가 고등학교 때 배운 수학에서는 1차원이었기 때문에, 함수의 미분을 이용해서 해당 점의 기울기를 바로 구할 수 있었습니다.

 

하지만 우리가 다루게 되는 문제들은 대부분 고차원의 데이터이기 때문에, 이러한 방식으로 기울기를 구할 수는 없습니다.

 

고차원에서는 gradient라고 하는 개념을 이용하게 되는데요, 이는 다변량 미적분에서 사용되는 개념입니다.

 

gradient는 입력값인 x와 같은 차원을 가지고 있으면서, 각 차원에 대한 편미분 값으로 구성되어 있어서 해당하는 좌표 방향으로 움직였을 때 함수의 기울기가 어떤지 알려줍니다.

 

gradient가 사용되는 이유 중 하나는, gradient의 기하학적인 의미 때문입니다. gradient는 함수가 가장 크게 상승하는 방향을 알려주기 때문에, gradient가 작아지는 방향을 구하게 되면 해당 함수가 가장 빠르게 작아지는 방향을 알 수 있게 됩니다. 

 

gradient에 대해서 궁금하시다면, 구글에서 조금 더 검색해보시면 다양한 자료들을 찾아보실 수 있을 겁니다.

 

한 번쯤은 gradient가 무엇인지에 대해서 공부해보시면 더더욱 좋을 것 같습니다.

 

 

 

 

 

 

Gradient를 실제로 계산하는 방법은 두 가지가 존재하는데, 먼저 첫 번째 방법인 Numeric Gradient를 보도록 하겠습니다.

 

현재 기울기 $W$가 왼쪽 첫 번째 column처럼 구성되어 있다고 한다면, 첫 번째 row에 해당하는 0.34에 매우 작은 양수인 0.0001을 더해줍니다.

 

다음으로 $f(x+h) - f(x) / h$를 계산해서, 해당 weight 값의 $dW$를 계산해주게 됩니다.

 

동일한 방식을 이용해서 weight의 각 값들에 대해서 $dW$를 계산해볼 수 있겠죠?

 

근데 보통 weight의 차원이 매우 크다는 점을 감안하면, 이렇게 계산하는 것은 너무나 느립니다. 왜냐하면 모든 차원의 값들을 전부 계산해야 하기 때문이죠.

 

 

 

 

 

따라서, 사람들은 Loss function을 $W$에 대해서 미분을 하는 방법을 이용해서 Gradient를 계산했습니다.

 

미분을 이용하면, 고차원의 데이터도 한 번에 계산을 할 수 있기 때문이죠.

 

 

 

 

 

요약하자면, Gradient를 계산하는 방법은 Numerical gradient와 Analytic gradient로 총 두 가지 방법이 존재하는데 실제로는 미분을 이용하는 Analytic gradient를 사용합니다.

 

물론 numerical gradient가 필요가 없는 것은 아닙니다. 우리가 짠 코드가 잘 맞는지 확인해보기 위해서 numerical gradient를 이용해 일종의 unit test를 진행하는 데 사용됩니다. 이를 gradient check라고 부른다고 합니다.

 

 

 

 

 

 

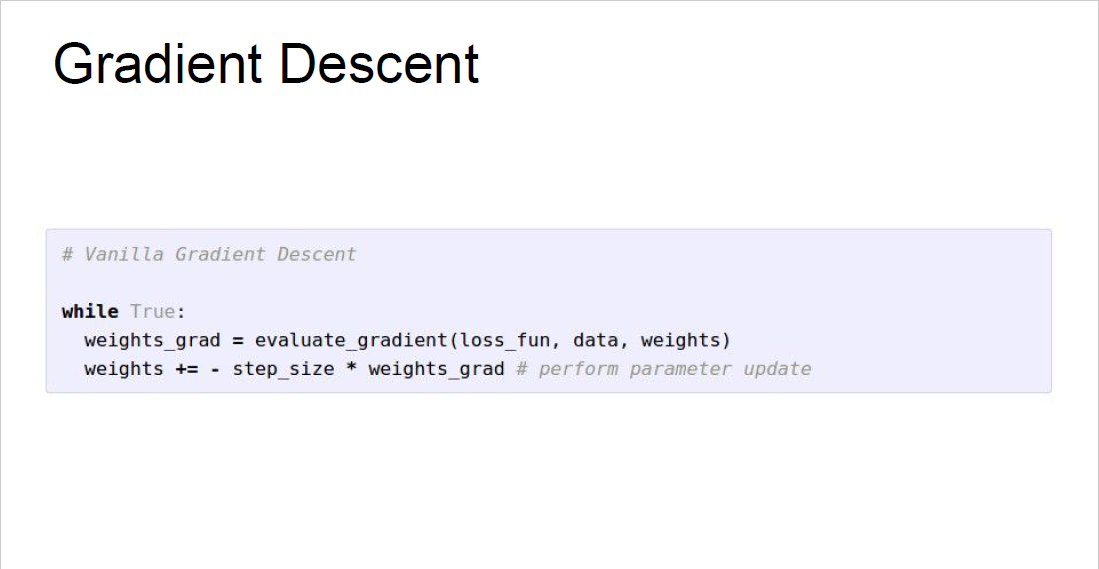
실제로 우리가 최적의 $W$를 구하기 위해서는 다음과 같은 방법을 이용해줍니다.

 

먼저 $W$를 랜덤 값으로 초기화해줍니다.

 

그러고 나서, 해당 $W$값을 이용해 loss를 계산해주고, loss function을 $W$로 미분하여 gradient를 계산합니다.

 

gradient가 loss를 가장 빠르게 높여주는 방향을 알려주기 때문에, 이에 -를 취해서 loss를 가장 빠르게 작아지는 방향을 찾습니다. 그리고 해당 방향으로 아주 작은 step 만큼만 이동합니다.

 

이러한 과정을 계속 반복하여, loss가 가장 작은 지점에 수렴하는 방법을 이용합니다.

 

이를 Gradient Descent라고 부릅니다.

 

위 슬라이드에서 step_size라고 하는 변수가 등장하는데, 이는 hyperparameter로 loss가 가장 빠르게 작아지는 방향으로 얼마큼 이동할 것인지 결정합니다. Learning rate라고 하는 용어로도 불립니다. 

 

아마 추후 강의에서 다룰 것이겠지만, step size를 너무 작게 주면, 훨씬 많이 반복해야 loss가 가장 작아지는 지점에 도달하게 되기 때문에 연산하는데 시간이 오래 걸리게 됩니다. 하지만 step size를 너무 크게 주게 되면, 아예 loss function이 발산해버릴 수도 있습니다. 따라서 step size(learning rate)를 얼마로 줄 것인지도 학습에 있어서 중요한 요소가 됩니다.

 

 

 

 

 

그림에서 빨간 부분이 loss가 작은 곳을 나타내고, 파란 부분이 loss가 큰 부분을 나타냅니다.

 

현재 있는 하얀 동그라미의 위치가 original W이며, 여기서 negative gradient 방향으로 이동하는 모습을 그림으로 표현한 것입니다.

 

 

 

 

 

하지만 Gradient Descent 방법을 전체 데이터에 대해서 계산하기에는 연산량이 매우 부담스럽습니다.

 

보통 데이터가 작으면 수천, 수만 개에서 크면 수백만, 수천만 개가 될 수 있습니다.

 

따라서, Gradient를 계산할 때 minibatch라고 하는 일부 데이터만 이용해서 계산해주고 이를 반복해서 계산해 전체 데이터에 대한 Gradient값의 추정치를 계산하는 방법이 바로 SGD라고 볼 수 있습니다.

 

minibatch는 관례적으로 2의 제곱 값을 이용하며 32개, 64개, 128개 등을 주로 사용합니다. 

 

강의자가 얘기하기로는, 이를 stochastic 하다고 이름 붙여진 이유가 바로 해당 방법이 전체 데이터에 대한 gradient값을 Monte Carlo 방식을 이용해서 구하기 때문이라고 합니다.

 

Monte Carlo가 무엇인지에 대해서는 다양한 자료들이 있으니, 찾아보시면 좋을 것 같습니다.

 

Monte Carlo의 대략적인 아이디어는, 수많은 샘플링을 통해서 어떠한 값의 근삿값을 찾아내는 방법론인데요. 현재 SGD가 하고 있는 작업과 사실상 동일합니다. 데이터 중 일부인 minibatch를 이용해서 gradient를 계산하는 작업을 여러 번 반복하여 전체 데이터의 gradient를 근사하는 것이지요.

 

 

 

 

 

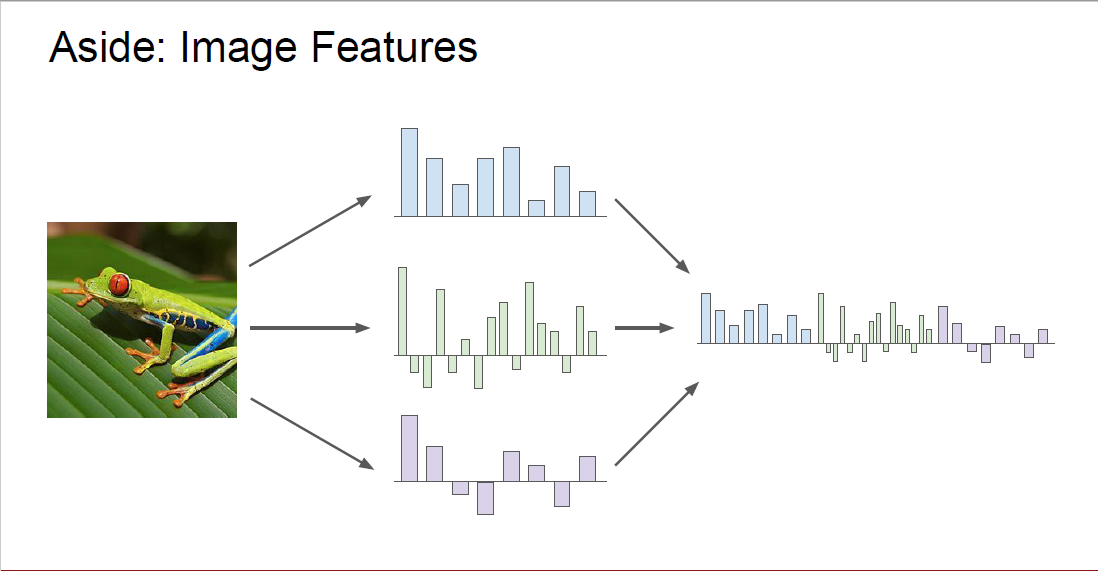
Optimization에 이어, 추가적으로 Image Feature와 관련된 내용들을 다루고 있습니다.

 

Deep learning을 사용하기 전에는 Image Feature를 어떻게 추출했는지를 설명하고 있는데요.

 

이미지의 raw pixel을 linear classifier에 넣어주게 되면 multi-modality 등의 문제에 대응할 수 없다는 한계점이 존재했기 때문에, 다음과 같은 two-stage 접근법이 요구되었습니다. 첫 번째로, 이미지의 모습과 관련된 다른 종류의 quantity를 계산하고, 두 번째로 이미지의 feature representation을 얻기 위해 첫 번째에서 구한 것들을 concat 시켰습니다.

 

마지막으로 구해진 feature representation을 linear classifier에 넣어서 이미지들을 분류하곤 했습니다.

 

그렇다면 사람들은 어떻게 이러한 Image Feature를 뽑아야 한다는 아이디어를 생각해냈을까요?

 

 

 

 

왼쪽의 그림을 보시게 되면, 빨간색 data point과 파란색 data point를 linear classifier를 이용해서는 분류할 수 없습니다.

 

하지만, feature transform을 이용해서 data들이 분포된 형태를 바꿔주게 되면, data point들을 linear classifier를 이용해서 분류할 수 있게 됩니다.

 

따라서 사람들은 이미지에 대해서 어떤 feature representation을 뽑아내게 되면, 오른쪽의 모습처럼 data point를 linear classifier를 이용해서 분류할 때 더 좋은 성능을 낼 수 있을 것이라고 생각하게 되었습니다.

 

그렇다면 deep learning이 사용되기 전에 사람들은 어떤 feature representation을 사용했을까요?

 

 

 

 

 

 

첫 번째 예시는 바로 Color Histogram입니다. 

 

색에 대한 스펙트럼을 bucket으로 나누고, 이미지에 존재하는 각 pixel에 대해서 해당 pixel이 어떤 bucket에 해당하는지를 count 합니다.

 

따라서 이를 이용하면, 이미지를 global 하게 봤을 때 어떤 컬러들로 분포되어 있는지를 확인할 수 있습니다.

 

 

 

 

두 번째 예시는 Histogram of Oriented Gradients (HoG)입니다. 

 

사람의 visual system에서 oriented edge가 중요한 역할을 하는데, HoG는 이러한 직관을 포착하려고 시도한 feature representation입니다.

 

강의자가 자세한 방법론을 설명해주진 않았지만, 대략 이미지를 여러 부분으로 localize 해서 각 부분이 어떤 종류의 edge로 구성되어 있는지를 판단해보는 방법이라고 이해해보면 좋을 것 같습니다.

 

슬라이드의 오른쪽 그림을 보면, 왼쪽 원본 그림의 edge를 잘 포착하고 있는 것을 확인할 수 있습니다.

 

자세하게 HoG를 어떻게 구하는지 궁금하시다면, 추가적으로 검색해보시는 것을 추천합니다.

 

 

 

 

 

 

세 번째 예시로는 Bag of Words를 사용하는 방법이 있습니다. 이는 Natural Language Processing에서 영감을 받은 아이디어인데요.

 

예를 들어서, 만약 문단을 표현하고 싶다면 해당 문단에 나타나는 단어들의 빈도를 count 해서 보여줄 수 있겠죠?

 

이러한 아이디어를 이미지에 적용해보는 시도입니다.

 

이미지의 각 patch들을 추출해서, 이를 visual word로 생각하고 k-means clustering 등의 방법을 이용해 군집을 형성해서 "codebook"을 만들어줍니다. 

 

codebook의 각각을 잘 보면, edge와 color를 추출하고 있는 것을 확인할 수 있습니다.

 

다음으로는, 이미지에 대해서 이러한 visual word가 얼마나 자주 나오는지를 count 하여 이미지의 feature representation을 얻을 수 있습니다.

 

 

 

 

 

Deep learning 이전에 사용했던, 5~10년 전에 사용한 Image feature와 현재 ConvNet과의 차이를 비교해보겠습니다.

 

기존에는 이미지에서 BoW나 HoG와 같은 Feature를 추출한 뒤, 이를 f로 표기된 linear classifier에 투입해 각 class에 대한 score를 얻는 방식을 이용하였습니다. Feature는 한 번 추출되면, training 하는 동안 바뀌지 않습니다. 학습이 진행되면 linear classifier만 업데이트되는 방식이었죠.

 

하지만 Deep learning의 경우는 ConvNet을 이용해서 Feature를 추출하게 되고, 학습이 진행될 때 feature를 추출하는 ConvNet도 학습되고, 추출된 feature를 이용해서 각 class의 class score를 예측하는 linear classifier도 학습되게 됩니다.

 

 

 

지금까지 cs231n의 lecture 3에 대해서 정리해보았고, 이번에도 내용을 정리해볼 수 있는 간단한 Quiz를 만들어보았습니다.

 

 

 

cs231n lecture 3 Quiz

 

 

Q1. loss function이 무엇이고, 어떤 의미를 가지고 있나요?

 

Q2. SVM loss와 softmax loss의 차이점은 무엇인가요?

 

Q3. L1 Regularization과 L2 Regularization의 식을 설명하고, 각 Regularization은 어떤 형태의 weight를 선호하는지 이야기해보세요.

 

Q4.

해당 케이스에 대해서 softmax loss를 직접 계산해보세요.

 

Q5. Gradient Descent에 대해서 설명해보고, Gradient Descent과 Stochastic Gradient Descent는 어떤 차이가 있는지 설명해보세요.

 

Q6. Deep learning을 이용해서 이미지 분류를 수행한 경우와, Deep learning을 이용하지 않고 직접 Feature를 추출해서 이미지 분류를 수행한 경우에 어떤 차이가 있는지 설명해보세요.