이번 내용은 다항 곡선 피팅에 대한 내용입니다. 즉, 데이터가 주어졌을 때 이를 잘 표현할 수 있는 다항 곡선을 만들어내는 것입니다.
실숫값의 입력 변수인 $x$를 관찰한 후 이 값을 바탕으로 실숫값인 타깃 변수 $t$를 예측하려 한다고 가정합니다.
예시에서 사용된 데이터는 $sin(2\pi{x})$ 함수를 사용하여 만들었으며, 타깃 변수에는 약간의 랜덤 노이즈를 포함했는데 이는 가우시안 분포 기반으로 표준편차 0.3을 사용하여 만들었습니다.
$N$개의 관찰값 $x$로 이루어진 훈련 집합 $\bf{x} \equiv$ $(x_1, ... x_N)^T$와 그에 해당하는 타깃 값 $\bf{t} \equiv$ $(t_1, ... t_N)^T$가 주어졌다고 생각해봅니다. 만약 N = 10이라면 다음과 같은 그림으로 표현할 수 있습니다.

입력 데이터 집합 $\bf{x}$는 서로 간에 같은 거리를 가지도록 균등하게 $x_n$값들을 선택해서 만들었다고 합니다.
우리가 패턴 인식 알고리즘을 통해 알아내고 싶은 실제 데이터 집합은 어떤 특정한 규칙성을 가지지만, 각각의 관찰 값들은 보통 랜덤한 노이즈에 의해 변질되곤 합니다. 이러한 노이즈는 본질적으로 확률적인 과정을 통해서 발생할 수 있으나, 더 많은 경우에는 관찰되지 않은 변수의 가변성에 기인한다고 합니다.
우리의 목표는 훈련 집합들을 통해 어떤 새로운 입력값 $\hat{x}$가 주어졌을 때 타깃 변수 $\hat{t}$를 예측하는 것입니다. 결국에는 기저에 있는 함수인 $sin(2\pi{x})$를 찾아내는 것이 예측 과정에 포함된다고 생각할 수 있습니다. 이는 한정적인 데이터 집합으로부터 일반화를 하는 과정이니 본질적으로 어려운 문제이며, 관측된 값이 노이즈에 의해 변질되어 있어서 더더욱 어려운 상황입니다.
곡선을 피팅하는데 있어서 다음과 같은 형태의 다항식을 활용합니다.
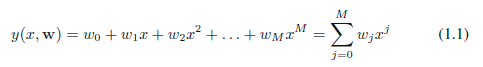
$M$은 다항식의 차수(order), 다항식의 계수인 $w_0, ... w_M$을 함께 모아서 벡터 $\bf{w}$로 표현할 수 있습니다. 다항 함수 $y(x, \bf{w}$$)$는 $x$에 대해서는 비선형이지만, 계수 $\bf{w}$에 대해서는 선형입니다. (선형이냐 아니냐는 1차 함수인지 아닌지를 생각해보시면 쉽습니다. 즉, $x$에 대해서는 2차, 3차... M차로 구성되지만, 계수인 $w_0$ 등은 차수가 1이기 때문에 선형이라고 부르는 것입니다. 계수를 기준으로 볼 때는 $x$는 실수 값처럼 생각해주시면 됩니다.)
우리가 식 1.1에서 정의한 다항식을 훈련 집합 데이터에 fitting해서 계수의 값들을 정할 수 있습니다. 훈련 집합의 타깃 값과 함숫값(다항식을 이용해서 예측한 값) $y(x, \bf{w}$$)$와의 오차를 측정하는 오차 함수(error function)를 정의하고 이 함수의 값을 최소화하는 방식으로 fitting 할 수 있습니다. 즉, 최대한 예측값이 실제 타깃 값과 가까워지게끔 하겠다는 것입니다. 가장 널리 쓰이는 간단한 오차 함수 중 하나는 식 1.2에서 보이는 것처럼 타깃 값과 함숫값 사이의 오차를 제곱해서 합산하는 함수를 사용합니다.

식 1.2의 함수에서 왜 갑자기 1/2이 추가되었나 라고 한다면, 추후 이 함수를 미분해야 하기 때문에 계산상으로 조금 더 편하게 하기 위해서 곱했다 정도로 생각해주시면 됩니다.(제곱 형태기 때문에, 미분 하면 2가 앞으로 나오게 되어 1/2를 상쇄하게 됩니다.) 해당 오차 함수는 결괏값이 0보다 크거나 같은 값이 나오게 되며, 오직 함수 $y(x, \bf{w}$$)$가 정확히 데이터 포인트들을 지날 때만 값이 0이 된다는 사실을 알 수 있습니다.
$E(\bf{w}$$)$를 최소화하는 $\bf{w}$를 선택함으로써 이 곡선 피팅 문제를 해결할 수 있으며, 식 1.2에서 주어진 오차 함수가 이차 다항식의 형태를 지니고 있으므로 이를 계수에 대해서 미분하면 $\bf{w}$에 대해 선형인 식이 나오게 됩니다. 이를 통해 오차 함수를 최소화하는 유일한 값인 $\bf{w}^*$를 찾아낼 수 있습니다.
아직 우리가 고려하지 않은 사항이 있습니다. 바로 다항식의 차수 $M$을 결정해야 합니다. 이 문제는 모델 비교(model comparison) 혹은 모델 결정(model selection)이라 불리는 중요한 내용입니다. 그림 1.4에서는 $M$ = 0, 1, 3, 9인 네 가지 경우에 대해 앞에서 언급한 데이터를 바탕으로 다항식을 피팅하는 예시를 보여줍니다.

우리가 피팅한 다항식은 빨간색으로, 실제 데이터에 사용된 기저 함수인 $sin(2\pi{x})$은 연두색으로, 데이터 포인트는 파란색 원으로 표시되어 있습니다.
여기서는 우리가 다항식의 차수를 어떻게 결정하는지에 따라 피팅된 곡선이 어떤 모습을 하게 되는지를 보시면 됩니다.
먼저 상수($M$ = 0)일 때와 1차($M$ = 1) 다항식을 사용할 때는 피팅이 잘 되지 않고 있는 모습을 확인할 수 있습니다. 이는 우리가 사용하려는 다항식이 너무 단순해서, 데이터 포인트를 충분히 표현하기에 어렵다는 것을 의미합니다. 책에는 이렇게 쓰여있지는 않지만, 모델의 복잡도가 낮다 라는 용어로도 표현합니다. 복잡도는 보통 영어로 complexity라고 표현하니 이 용어를 알아두시면 좋습니다.
3차($M$ = 3) 다항식의 경우는, 기저 함수를 잘 표현하고 있음을 확인할 수 있습니다.
차수를 더 높여 9차($M$ = 9) 다항식을 사용할 경우, 훈련 집합에 대한 완벽한 피팅이 가능합니다. 이 경우 피팅된 곡선이 모든 데이터 포인트를 지나가며 앞에서 정의한 오차 함수 기준으로 $E(\bf{w^*}$$) = 0$입니다. 하지만 피팅된 곡선은 심하게 진동하고 있고, 함수 $sin(2\pi{x})$를 적절하게 표현하지 못하고 있습니다. 이것이 바로 과적합(over-fitting)의 예시입니다.
앞에서 언급했듯이, 우리의 목표는 새로운 데이터가 주어졌을 때, 정확한 결괏값을 예측할 수 있는 좋은 일반화를 달성하는 것입니다. 따라서, 이러한 과적합을 피해야 합니다.
앞과 같은 과정을 사용하되, 랜덤한 노이즈 값만 다르게 적용해 100개의 새 데이터 포인트로 이루어진 시험 집합을 만들어 봅니다. 이 시험 집합에서의 성능을 확인해 보면 $M$의 값에 따라 일반화의 성능이 어떻게 변화하는지 정량적으로 살펴볼 수 있습니다.
훈련 집합과 시험 집합 각각에 대해서 평균 제곱근 오차(root mean square error, RMSE)를 이용해 일반화의 성능을 확인해봅시다. RMSE는 다음과 같이 정의됩니다.

$N$으로 나눠 데이터 사이즈가 다른 경우에도 비교할 수 있으며, 제곱근을 취해 RMSE가 정답 값 $t$와 같은 크기를 가지게 됩니다.
각각의 $M$ 값에 대한 훈련 집합과 시험 집합의 RMSE를 그림 1.5에서 확인할 수 있습니다.

$M$ 값이 작은 경우는 시험 오차가 상대적으로 큽니다. 즉 낮은 차수의 다항식은 비교적 융통성이 없어 피팅된 다항식이 기저인 함수를 충분히 표현할 수 없습니다.
$3 \leq M \leq 8$의 경우, 시험 집합의 오차가 작고 피팅된 해당 다항식이 기저인 함수를 충분히 잘 표현하고 있습니다.
$M = 9$일 경우는 훈련 집합의 오차가 0이지만, 시험 집합의 오차가 굉장히 큽니다.
차수 $M$에 따른 피팅 함수의 계수 $\bf{w}^*$의 값들을 적은 표 1.1도 한번 봅시다.

$M$이 커짐에 따라 계숫값의 단위 역시 커지는 것을 확인할 수 있습니다. 특히, $M = 9$ 다항식의 경우는 상당히 큰 양숫값의 계수와 음숫값의 계수가 번갈아 나타나는 것을 볼 수 있습니다. 이는 각각의 데이터 포인트에 정확하게 맞도록 피팅한 결과죠.
사용되는 데이터 집합의 크기가 달라지는 경우에는 어떤 일이 일어나는지 확인해 봅시다. 그림 1.6를 보면 이에 대해 생각해볼 수 있습니다.

모델의 복잡도를 일정하게 유지시킬 때는 사용하는 데이터 집합의 수가 늘어날수록 과적합 문제가 완화되는 것을 확인할 수 있습니다. 이를 다르게 표현하면 데이터 집합의 수가 클수록 더 복잡한 모델을 활용하여 피팅할 수 있다는 의미도 됩니다.
비교적 복잡하고 유연한 모델을 제한적인 숫자의 데이터 집합을 활용하여 피팅하려면 어떻게 하는게 좋을까요?
과적합 문제를 해결하기 위해 자주 사용되는 기법 중 하나가 바로 정규화(regularization) 입니다. 기존의 오차 함수에 피팅 함수의 계수 크기가 커지는 것을 막기 위해 페널티항을 추가하는 것입니다. 이러한 페널티항 중 가장 단순한 형태는 각각의 계수들을 제곱하여 합하는 것이며, 이는 다음 식 1.4처럼 표현할 수 있습니다.

여기서 패널티항은 $\parallel w \parallel^2$ $\equiv$ $\bf{w}^T{w}$ = $w^2_0 + w^2_1 + .... w^2_M$이며, 여기서 사용된 계수 $\lambda$는 제곱합 오류항에 대한 상대적인 중요도를 결정합니다.
통계학 문헌들에서는 이 방법을 수축법(shrinkage method)라고 합니다. 방법 자체가 계수의 크기를 수축시키는 방식을 이용하기 때문이죠. 이차 형식(quadratic) 정규화는 리지 회귀(ridge regression)이라고 부릅니다. 딥러닝에서는 이를 가중치 감쇠(weight decay)라고 합니다.
그림 1.7을 보면 계수 $\lambda$의 값에 따른 $M = 9$ 다항식을 피팅한 결과를 확인할 수 있습니다.

$ln\lambda$ = -18의 경우 과적합이 많이 줄어들었고, 그 결과 다항식이 기저 함수에 훨씬 더 가까워진 것을 확인할 수 있습니다. 하지만, 너무 큰 $\lambda$ 값을 사용하면 좋지 않은 피팅 결과를 가져옵니다. 이는 그림 1.7의 오른쪽 그림을 통해서 확인할 수 있습니다.
표 1.2에는 해당 피팅 다항식의 계숫값들이 나타나 있습니다.
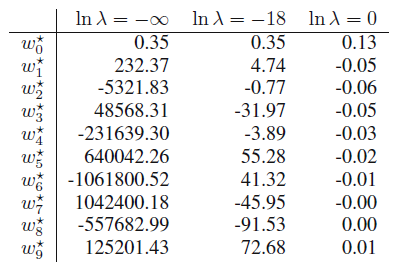
$ln\lambda$ = $- \infty$ 인 경우는 $\lambda$ = 0인 경우이고, $ln\lambda$ = 0인 경우는 $\lambda$ = $e$인 경우입니다. 즉, 왼쪽에서 오른쪽으로 갈수록 $\lambda$가 더 커지는 것으로 이해할 수 있습니다.
확실히 $\lambda$가 커질수록, 정규화의 효과가 나타나는 것을 확인할 수 있습니다. 계수가 엄청나게 줄어들었죠.
그림 1.8에는 서로 다른 $ln\lambda$ 값에 따라서 훈련 집합과 시험 집합의 RMSE의 변화를 확인할 수 있습니다. $\lambda$가 모델의 복잡도를 조절해서 과적합 정도를 통제하는 것을 확인할 수 있습니다.

지금까지의 내용을 정리해보면, 결국 오차 함수를 줄이는 방식으로 다항식을 피팅하는 경우에는 과적합 문제를 해결하기 위해서는 적합한 정도의 모델 복잡도를 선택하는 방법을 잘 활용해야 한다는 것입니다.
지금까지의 결과를 바탕으로 모델 복잡도를 잘 선택하는 단순한 방법 하나를 생각해 볼 수 있는데, 이는 바로 데이터 집합을 훈련 집합(training set)과 검증 집합(validation set, hold-out set)으로 나누는 것입니다.
훈련 지합은 계수 $\bf{w}$를 결정하는 데 활용하고, 검증 집합은 모델 복잡도($M$나 $\lambda$)를 최적화하는 데 활용하는 방식입니다. 하지만 많은 경우에 이 방식은 소중한 훈련 집합 데이터를 낭비하게 됩니다. 따라서 더 좋은 방법을 고려할 필요가 있습니다.
지금까지 다항 곡선을 피팅하는 문제에 대해서 논의해보았으며, 다음 절에서는 확률론에 대해서 살펴보도록 합니다.
1.1절 간단하게 정리
- 데이터를 잘 표현하기 위해서, 오차 함수를 정의하고 오차 함수가 최소가 되는 가중치 $\bf{w}$를 결정합니다.
- 이 때, 적절하게 다항 함수의 차수와 가중치의 크기를 조절해야만 과적합이 일어나지 않습니다. 주로 정규화를 이용해서 이를 조절할 수 있습니다.
- 아니면 학습을 할 때, 더 많은 데이터를 사용하면 과적합을 피할 수 있습니다.
'딥러닝 & 머신러닝 > PRML' 카테고리의 다른 글
| PRML(패턴인식과 머신러닝) - Chapter 1. (3) Model Selection(모델 선택) (0) | 2021.02.28 |
|---|---|
| PRML(패턴인식과 머신러닝) - Chapter 1. (2) Probability Theory(확률론)(2) (0) | 2021.02.28 |
| PRML(패턴인식과 머신러닝) - Chapter 1. (2) Probability Theory(확률론)(1) (0) | 2021.02.27 |
| PRML(패턴인식과 머신러닝) - Chapter 1. (0) Prologue (0) | 2021.02.24 |