텐서플로와 머신러닝으로 시작하는 자연어 처리 - Chapter 3. 자연어 처리 개요(1)

2019. 11. 22. 15:36

(티스토리 임시저장 기능 믿고 임시저장 했다가 글이 전부 날라가서 전부 다시 다 쓰고 있습니다.... 혹시나 티스토리를 이용하려는 분이 있다면 반드시 비공개로라도 글을 작성해두시는걸 추천합니다...)

이번 Chapter 3에서는 자연어 처리에 대한 전반적인 내용에 대해 알아본다.

이번 장에서는 총 4개의 문제에 대해서 알아볼탠데, 4개의 문제란 (1) 텍스트 분류, (2) 텍스트 유사도, (3) 텍스트 생성, (4) 기계이해로 자연어 처리의 핵심 문제에 해당한다. 여기서는 자연어 처리를 통해 어떤 문제를 해결할 수 있고, 어떤 방식으로 해결하는지 알아보려고 한다.

앞서 소개한 4가지 문제에 대해서 알아보기 전에, 단어 표현 이라는 분야에 대해서 먼저 알아본다. 단어 표현은 모든 자연어 처리 문제의 기본 바탕이 되는 개념으로, 자연어를 어떻게 표현할지 정하는 것이다.

<1> 단어 표현

자연어 처리는 컴퓨터가 인간의 언어를 이해하고 분석 가능한 모든 분야를 말한다. 따라서 자연어 처리의 가장 기본적인 문제는 '어떻게 자연어를 컴퓨터에게 인식시킬 수 있을까?' 이다.

기본적으로 컴퓨터가 텍스트를 인식하는 방법은 텍스트를 '유니코드' 혹은 '아스키 코드' 라는 방법을 이용해서 인식한다.

예를 들면 언 이라는 단어가 있다면, 이를 이진화된 값(예를 들어 11010101010) 으로 인식하는 것이다.

하지만 자연어 처리에 이 방식을 그대로 사용하기에는 언어적인 특성을 반영하지 않는다는 점에서 부적절하다.

그럼 어떤 방식으로 텍스트를 표현해야 자연어 처리 모델에 적용할 수 있는가?

이러한 질문의 답을 찾는 것이 단어 표현(Word Representation) 분야 이다. 텍스트를 자연어 처리를 위한 모델에 적용할 수 있게 언어적인 특성을 반영해서 단어를 수치화하는 방법을 찾는 것이다. 그리고 이렇게 단어를 수치화할 때는 단어를 주로 벡터로 표현한다. 따라서 단어 표현을 단어 임베딩(Word Embedding) 혹은 단어 벡터(Word Vector)라고 표현하기도 한다. 단어 표현에는 다양한 방법이 있고 계속해서 연구되고 있는 분야이기 때문에 하나의 정답이 있는 것은 아니지만 이 책에서는 많이 사용하는 방법 위주로 하나씩 알아본다.

단어를 표현하는 가장 기본적인 방법은 원-핫 인코딩(one-hot encoding) 방식이다. 단어를 하나의 벡터로 표현하는 방법인데, 각 값은 0과 1만 갖는다. 예를 들어서 4개의 단어(사과, 딸기, 개, 고양이)가 있다면 사과는 [1, 0, 0, 0], 딸기는 [0, 1 , 0, 0]과 같은 방식으로 표현하는 것이다. 방법 자체가 매우 간단하고 이해하기가 쉬운 장점이 존재한다.

하지만, 원-핫 인코딩 방식이 가지고 있는 결정적인 두 가지 문제점이 있는데,

첫번째, 실제 자연어 처리 문제를 해결할 때에는 수십만, 수백만 개가 넘는 단어를 표현해야 하므로 단어 벡터의 크기가 너무 커져 공간을 많이 사용하게 되고, 큰 공간에 비해 실제로 사용하는 값은 1이 되는 값 하나뿐이므로 매우 비효율적이다.

두번째, 원-핫 인코딩 방식은 단순히 단어가 무엇인지만 알려줄 수 있고, 벡터값 자체에는 단어의 의미나 특성 같은 것들이 전혀 표현되지 않는다는 점이다.

위에서 언급된 두가지 원-핫 인코딩 방식의 문제점을 해결하기 위해서 다른 인코딩 방법들이 제안되었다. 즉, 벡터의 크기가 작으면서도 벡터가 단어의 의미를 표현할 수 있는 방법들인데, 이러한 방법들은 분포 가설(Distributed hypothesis)을 기반으로 한다. 분포 가설이란, "같은 문맥의 단어, 즉 비슷한 위치에 나오는 단어는 비슷한 의미를 가진다"라는 개념이다.

따라서 어떤 글에서 비슷한 위치에 존재하는 단어는 단어 간의 유사도가 높다고 판단하는 방법인데, 크게 두 가지 방법으로 나뉜다.

첫번째, 특정 문맥 안에서 단어들이 동시에 등장하는 횟수를 직접 세는 방법인 카운트 기반(count-base)

카운트 기반 방법으로 단어를 표현한다는 것은 어떤 글의 문맥 안에 단어가 동시에 등장하는 횟수를 세는 방법이다. 여기서 동시에 등장하는 횟수를 동시 출현 또는 공기라고 부르고 영어로는 Co-occurrence라고 한다. 카운트 기반 방법에서는 기본적으로 동시 등장 횟수를 하나의 행렬로 나타낸 뒤, 그 행렬을 수치화해서 단어 벡터로 만드는 방법을 사용하는 방식인데 다음과 같은 방법들이 있다.

- 특이값 분해(Singular Value Decomposition, SVD)

- 잠재의미분석(Latent Semantic Analysis, LSA)

- Hyperspace Analogue to Langauge(HAL)

- Hellinger PCA(Principal Component Analysis)

위의 네 가지 방법은 모두 동시 출현 행렬(Co-occureence matrix)를 만들고 그 행렬들을 변형하는 방식인데, 이 책에서는 동시 출현 행렬까지만 만들어 보고 행렬을 통해 다시 단어 벡터로 만드는 방법에 대해서는 다루지 않는다. (따로 찾아봐야 한다는 얘기인듯하다.)

우선 다음 예시를 가지고 동시 출현 행렬을 만들어 보자.

- 성진과 창욱은 야구장에 갔다.

- 성진과 태균은 도서관에 갔다.

- 성진과 창욱은 공부를 좋아한다.

위의 3개의 문장을 가지고 동시 출현 행렬을 만들어본다면 다음과 같이 만들 수 있다.

	성진과	창욱은	태균은	야구장에	도서관에	공부를	갔다.	좋아한다.
성진과	0	2	1	0	0	0	0	0
창욱은	2	0	0	1	0	1	0	0
태균은	1	0	0	0	1	0	0	0
야구장에	0	1	0	0	0	0	1	0
도서관에	0	0	1	0	0	0	1	0
공부를	0	1	0	0	0	0	0	1
갔다.	0	0	0	1	1	0	0	0
좋아한다.	0	0	0	0	0	1	0	0

이렇게 만들어진 동시 출현 행렬을 토대로 4가지 방법등을 사용하여 단어 벡터를 만들면 된다.

카운트 기반 방법의 장점은 빠르다는 점이고, 예측 방법에 비해 좀 더 이전에 만들어진 방법이지만 데이터가 많을 경우에는 단어가 잘 표현되고 효율적이어서 아직까지도 많이 사용하는 방법이다.

두번째, 신경망 구조 혹은 어떠한 모델을 사용해 특정 문맥에서 어떤 단어가 나올지 예측하는 예측 방법(Predictive)

예측 방법에는 다음과 같은 것들이 존재한다.

- Word2Vec

- NNLM(Neural Network Language Model)

- RNNLM(Recurrent Neural Network Language Model)

여러 예측 기반 방법 중에서 단어 표현 방법으로 가장 많이 사용되는 Word2Vec에 대해 자세히 알아본다.

Word2Vec은 CBOW(Continuous Bag of Words)와 Skip-Gram이라는 두 가지 모델로 나뉜다. 두 모델은 각각 서로 반대되는 개념으로 생각하면 되는데, CBOW의 경우 "문맥 안의 주변 단어들을 통해 어떤 단어를 예측하는 방법"이고, 반대로 Skip-Gram의 경우 "어떤 단어를 가지고 특정 문맥 안의 주변 단어들을 예측하는 방법"이다.

예시를 들어서 CBOW와 Skip-Gram을 이해해보자.

- 민수는 냉장고에서 음식을 꺼내서 먹었다.

CBOW은 주변 단어를 통해 하나의 단어를 예측하는 모델인데, 이를 이용한다면 다음 문장의 빈칸을 채울 수 있다.

- 민수는 냉장고에서 _______ 꺼내서 먹었다.

반대로, Skip-Gram은 하나의 단어를 가지고 주변에 올 단어를 예측하는 모델인데, 이를 이용한다면 다음 문장의 빈칸을 채울 수 있다.

- _____ _____________ 음식을 ______ ________

그렇다면 CBOW와 Skip-Gram이 어떤 순서로 학습되는지 알아보도록 하자.

CBOW의 경우는 다음과 같은 순서로 학습한다.

1. 각 주변 단어들을 원-핫 벡터로 만들어 입력값으로 사용한다.

2. 가중치 행렬(weight matrix)을 각 원-핫 벡터에 곱해서 N-차원 벡터를 만든다.

3. 만들어진 N-차원 벡터를 모두 더한 후 개수로 나눠 평균 N-차원 벡터를 만든다.

4. N-차원 벡터에 다시 가중치 행렬을 곱해서 원-핫 벡터와 같은 차원의 벡터로 만든다.

5. 만들어진 벡터를 실제 예측하려고 하는 단어의 원-핫 벡터와 비교해서 학습한다.

책에는 이렇게 나와있었지만, 사실 CBOW를 5줄로 해서 이해하기란 어려울 것이다. 나 또한 이것을 읽고 그저 너무 겉핥기식으로 설명했다고 생각했다.

그래서 나는 CBOW와 관련된 글들을 추가적으로 읽고, 이것을 좀 더 상세히 풀어서 설명해보면 좋겠다는 생각을 했다.

따라서 다음에 나올 내용은 CBOW를 위에 언급된 5가지 순서를 지키되, 상세하게 어떤식으로 작동하게 되는지를 설명해보고자 한다.

이해를 돕기 위해 특정 예시를 들어서 설명을 하고자 하는데, 다음과 같은 예시를 사용한다.

예시 문장: 지금 너무 추워서 꼭 패딩 입어야 해(7글자)

CBOW는 주변 단어를 통해 하나의 단어를 예측하는 모델이라고 위에서 설명하였는데, 책에서는 언급이 되지 않았지만 꼭 고려해야 할 사항은 바로 주변 단어를 몇개로 잡을 것이냐의 문제이다. 즉, 주변에 있는 모든 단어를 사용하는 것이 아닌, 특정 몇 개의 단어를 이용해서 하나의 단어를 예측한다는 것이다. 주변 단어를 몇개로 잡을 것인지를 윈도우(window) 라는 단어로 표현하는데, 예시 문장에 윈도우를 2로 설정하였을 때 어떤 식으로 예측하게 되는지를 설명해보도록 하겠다. 파란색은 입력값으로 들어가는 단어, 빨간색은 예측을 하는 단어이다.

1. 지금 너무 추워서 꼭 패딩 입어야 해

2. 지금 너무 추워서 꼭 패딩 입어야 해

3. 지금 너무 추워서 꼭 패딩 입어야 해

4. 지금 너무 추워서 꼭 패딩 입어야 해

5. 지금 너무 추워서 꼭 패딩 입어야 해

6. 지금 너무 추워서 꼭 패딩 입어야 해

7. 지금 너무 추워서 꼭 패딩 입어야 해

예측 하려고 하는 단어(빨간색)의 양 옆으로 2개의 단어를 사용하여 예측하는 것을 볼 수 있을 것이다.

이런식으로 CBOW는 진행이 된다고 생각하면 된다.

가장 먼저 해볼 것은 CBOW의 전체적인 구조를 설명해볼 것이다. 상세한 내용은 차차 설명할 것이고, 전체적인 조망을 하기 위해 전체적인 구조를 먼저 설명하고자 한다.

먼저 첫번째 순서(1. 각 주변 단어들을 원-핫 벡터로 만들어 입력값으로 사용한다.)를 적용하면, 예시 문장을 각각 원-핫 벡터로 만들어준다. 즉 지금 = [1, 0, 0, 0, 0, 0, 0]으로, 너무 = [0, 1, 0, 0, 0, 0, 0], 꼭 = [0, 0, 0, 1, 0, 0, 0], 패딩 = [0, 0, 0, 0, 1, 0, 0]으로 만들어준다. 그리고 나서 이 입력값에 가중치 행렬을 곱해서 N-차원의 은닉층을 만들어낸다. 현재 예시에서는 4개를 입력값으로 넣었으므로, 4개의 N-차원 은닉층이 생기게 될 것이다. 이 4개의 N-차원 은닉층을 평균을 취해 평균 N-차원 은닉층을 만든 뒤, 여기에 새로운 가중치 행렬을 곱해서 출력층을 만들고, 여기에 Sigmoid를 적용해 모든 값들을 0 ~ 1 사이의 값으로 만든 뒤에 가장 큰 값을 가지는 요소를 정답으로 출력하게 된다.

이제부터 전체적인 구조를 조목조목 나누어 하나하나 세세하게 볼 것이다.

그 다음으로는 두번째 순서(2. 가중치 행렬(weight matrix)을 각 원-핫 벡터에 곱해서 N-차원 벡터를 만든다.)를 적용해 보아야 할탠데, 가중치 행렬은 크기가 어떻게 되고, 어떻게 곱해지는 것인지를 설명해보겠다.

현재 예시에서는 입력값이 1 x 7 크기의 행렬이므로, 가중치 행렬과 곱하려면 7 x N 형태의 벡터가 필요하다.

N 으로 하면 잘 와닿지 않을 것이므로, 이 글에서는 N을 4로 두고, 4차원 은닉층을 만드는 것으로 생각해보자.

그렇다면 가중치 행렬은 7 x 4 형태가 될 것이며, 이는 다음과 같이 곱해질 것이다.

가중치 행렬이 곱해지는 것을 보여주기 위해서, 7 x 4 형태의 matrix를 구성하고 값은 무작위의 정수로 채워넣었다.

실제로 CBOW가 학습되는 과정에서는 이 가중치 행렬은 정답을 가장 잘 맞출 수 있게끔 값이 학습될 것이다.

가중치 행렬을 곱하면 결과는 4차원의 은닉층이 될 것이고, 사이즈는 1 x 4가 되는 것을 볼 수 있다.

다음으로 세번째 순서(3. 만들어진 N-차원 벡터를 모두 더한 후 개수로 나눠 평균 N-차원 벡터를 만든다.)를 실제로 적용해보도록 하겠다.

그림 2와 그림 3에서 만들어낸 4개의 은닉층을 모두 더한 뒤, 이를 입력층의 크기인 4로 나누어 평균 은닉층을 구한 모습이다.

그 다음으로는 네번째 순서(4. N-차원 벡터에 다시 가중치 행렬을 곱해서 원-핫 벡터와 같은 차원의 벡터로 만든다.)를 실제로 적용해보도록 하겠다.

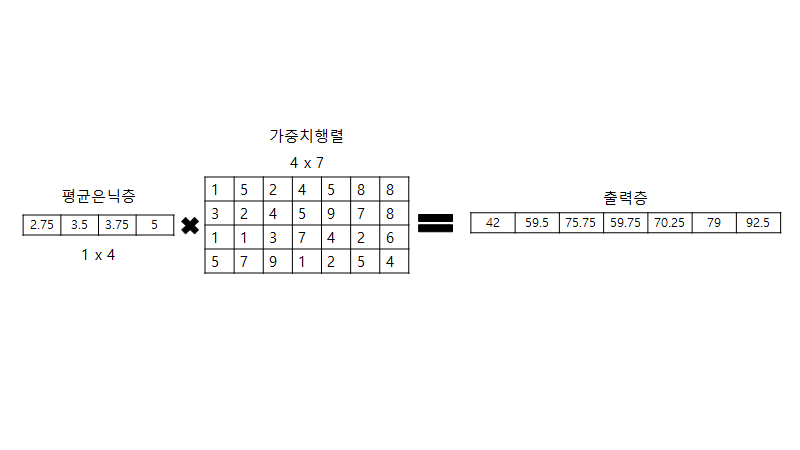
그림 4에서 구한 평균 은닉층에다가 가중치 행렬 4 x 7 사이즈를 곱해서 기존의 입력값인 1 x 7 형태의 출력층을 만들어낸다. 왜 출력층이 다시 1 x 7 형태로 되게끔 만들어야 하나? 라고 한다면 결국 우리가 원하는 것은 우리의 모델이 추워서 = [0, 0, 1, 0, 0, 0, 0]를 정답으로 내야 하기 때문에, 우리가 원래 사용했던 벡터의 크기와 동일한 크기의 벡터가 출력으로 나와야 하는 것이다.

그림 5에서 구한 출력층의 값들은 경우에 따라서 매우 클 수도 있고, 작을 수도 있는데 우리가 원하는 것은 가장 큰 값을 가지는 값을 찾아야 하는 것이기 때문에, 여기에 Sigmoid 함수를 적용시켜 모든 벡터의 값들을 0 ~ 1 의 값으로 바꾼다.

그렇게 했을때 가장 큰 값이 정답이 될 것이다. (그림 5에서는 가장 마지막 벡터가 Sigmoid를 적용했을때 가장 큰 값일 것이므로 정답으로 나오게 될 것이다. 물론 이번 예시에서는 임의의 가중치 행렬을 사용했기 때문에 틀린 정답이 나오게 되었다.)

여기서 사용된 두번째 가중치 행렬 또한 학습 과정에서 적절한 값으로 학습이 되는 것으로 생각하면 된다.

마지막 순서(5. 만들어진 벡터를 실제 예측하려고 하는 단어의 원-핫 벡터와 비교해서 학습한다.)는 손실 함수로 Cross-Entropy 오차를 사용한다.

0 ~ 1 출력층은 Sigmoid가 적용되어 모든 벡터들이 0과 1사이의 값이 되고, 이는 예측값이므로 y hat으로 표기하였다. 또 실제 정답은 추워서 [0, 0, 1, 0, 0, 0, 0] 이므로 이는 y로 표현하였다.

Cross-entropy가 왜 이런 식으로 구성되어 있는지에 대해서는 다른 글을 참고해보심이 좋을듯 하고, 여기서는 CBOW의 학습 과정에서 Loss function으로 Cross-entropy를 이용하여 학습한다는 점만 짚고 넘어가면 될듯 하다!

여기까지가 CBOW에 관련된 세부적인 설명이 되었다.

중간중간에도 썼지만, 결국 CBOW가 학습을 통해서 값을 찾아나가는 것은 바로 두개의 가중치 행렬이다. 즉 가장 정답을 잘 맞출 수 있는 가중치 값들로 점차적으로 학습해나간다는 말이다.

글이 너무 길어진 것 같아서, 여기서 한번 끊어주고 다음 글에서는 Skip-Gram에 대한 설명과 그 이후 내용들을 다뤄보도록 하겠다.

글을 마치기 전에, 이 내용을 읽었다면 다시 한번 정리해볼만한 내용들을 적어보고 이것들에 어느정도 답할 수 있다면 잘 기억하고 있다고 생각할 수 있을듯 하다.

첫번째 - 단어 임베딩 혹은 단어 표현 이라고 하는 분야는 왜 필요한가?

두번째 - 원-핫 인코딩 방식의 단어 표현이 가진 두 가지 문제점은 무엇인가?

세번째 - 분포 가설(Distributed hypothesis)란 무엇인가?

네번째 - 분포 가설을 기반으로 한 방법 두 가지는 각각 무엇인가?

다섯번째 - Word2Vec은 두 가지 모델로 나뉘는데, 각각 모델의 이름과 모델이 작동하는 방법은 무엇인가?

여섯번째 - CBOW의 전반적인 구조를 설명하라.

'딥러닝 & 머신러닝 > 자연어 처리' 카테고리의 다른 글

텐서플로와 머신러닝으로 시작하는 자연어 처리 - Chapter 3. 자연어 처리 개요(3) (0)	2020.02.06
텐서플로와 머신러닝으로 시작하는 자연어 처리 - Chapter 3. 자연어 처리 개요(2) (0)	2019.11.22
텐서플로와 머신러닝으로 시작하는 자연어 처리 - 소개 및 다짐 (0)	2019.11.22

헤헤