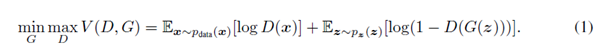헤헤

 

 

오늘은 Generative Adversarial networks에 Convolutional neural network를 섞은 모델인 DCGAN에 대해서 리뷰를 해보겠습니다.

 

original paper : arxiv.org/abs/1511.06434

 

Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks

In recent years, supervised learning with convolutional networks (CNNs) has seen huge adoption in computer vision applications. Comparatively, unsupervised learning with CNNs has received less attention. In this work we hope to help bridge the gap between

arxiv.org

 

사실 GAN에 CNN을 섞은 것 자체에 대한 내용은 알고 있었는데, 논문을 읽으면서 단순히 그냥 CNN을 섞은 것이 끝이 아니라 GAN이 학습한 representation에 대해서 탐구해봤다는 점에서도 의미가 있는 논문이라고 생각했습니다.

 

 

시작해보겠습니다.

 

 

Abstract

 

 

최근에, CNN을 활용한 지도 학습은 computer vision applications에서 많이 채택되고 있다. 하지만, 비교적 CNN을 활용한 비지도 학습은 적은 관심을 받고 있다.

 

본 연구에서 우리는 지도 학습에 대한 CNN의 성공과 비지도 학습 사이의 격차를 해소하는데 도움이 되길 바란다.

 

우리는 아키텍처의 제약을 가지고 있는 deep convolutional generative adversarial networks (DCGANs)라고 불리는 CNN의 일종을 도입하며, 이것이 비지도 학습을 위한 강력한 후보 모델임을 검증했다.

 

다양한 이미지 데이터셋에 학습해서, 우리의 deep convolutional adversarial pair가 generator와 discriminator 모두에서 object 부분부터 장면까지 representation의 계층을 학습한다는 확실한 증거를 보여준다.

 

추가적으로, 새로운 task를 위해 학습된 feature를 사용하였으며, 이를 통해 general image representation으로써의 이들의 적용 가능성을 검증하였다.

 

 

1. Introduction

 

 

많은 양의 unlabeled dataset으로부터 재사용할 수 있는 feature representation을 학습하는 것은 활발하게 연구가 이뤄지고 있는 분야이다.

 

Computer Vision의 맥락에서, 이는 good intermediate representation을 학습하기 위해서 사실상 무제한의 unlabeled image와 video를 활용할 수 있게 해 주며, good intermediate representation은 image classification과 같은 다양한 지도 학습 task에 사용될 수 있다.

 

우리는 GAN을 학습시키는 것을 통해 good image representation을 만드는 방법을 제안하며, 후에 지도 학습 task를 위한 feature extractor로써 generator network와 discriminator network의 일부분을 재사용할 수 있다.

 

GANs은 maximum likelihood techniques에 대한 매력적인 대안을 제공한다.

 

추가적으로 그들의 학습 과정과 heuristic cost function (pixel-wise independent mean-square error와 같은)이 없다는 점에서 representation learning에 매력적이라고 주장할 수 있다.

 

GANs는 학습하는 것이 불안정하다고 알려져 있으며 종종 generator에서 터무니없는 output을 생산해내기도 한다.

 

GNA이 학습하는 것, 그리고 multi-layer GANS의 중간 representation에 대해서 이해하고 시각화하려는 시도에 대해서는 매우 제한적인 연구만 존재한다.

 

본 연구에서는 다음과 같은 contribution이 있다.

 

• 대부분의 환경에서 학습이 안정적이게 만들어주는 Convolutional GANs의 architectural topology에 대한 일련의 제약을 제안하고, 평가한다. (아키텍처를 만들 때 어떤 걸 해도 되는지, 안되는지에 대해서 앞으로 나오게 되는데 이를 의미합니다.)
• GANs에 의해서 학습된 filter를 시각화하고 특정 필터가 특정 object를 그리는 방법을 학습했음을 경험적으로 보여준다.
• 우리는 generator가 생성된 샘플의 많은 의미적 특징을 쉽게 조작할 수 있는 흥미로운 벡터 연산 특성을 가지고 있음을 보여준다.

 

2. Related work

 

 

2.1 Representation learning from unlabeled data

 

 

unsupervised representation learning은 이미지의 맥락에서, 그리고 일반적인 컴퓨터 비전 연구에서 잘 연구된 문제이다.

 

Unsupervised representation learning에 대한 전통적인 접근법은 데이터에 대해서 clustering을 하고(예를 들면, K-means와 같은 방법을 사용해서), classification score를 향상하기 위해 이 cluster를 사용하는 것이다. 

 

이미지의 맥락에서, 강력한 image representation을 학습하기 위해서 image patch들의 계층적 클러스터링을 할 수 있다.

 

또 다른 일반적인 방법은 코드의 구성 요소인 이미지를 compact 코드로 인코딩하는 래더 구조를 분리하여 autoencoder를 학습시키는 것이며, 가능한 정확히 이미지를 복원하기 위해서 코드를 decode 한다. (사실 이걸 읽고 명확하게 이해는 안 되지만, 선행 연구 쪽이라서 그냥 넘어갔습니다..)

 

이러한 방법들은 또한 이미지 픽셀로부터 good feature representation을 학습할 수 있다고 알려져 있다.

 

Deep belief networks는 또한 계층적 표현을 학습하는데 있어서 잘 작동한다고 알려져 왔다.

 

 

 

2.2 Generating natural images

 

 

 

이미지 생성 모델은 잘 연구되어 왔으며 parametric과 non-parametric의 두 가지 범주로 나뉜다.

 

먼저, non-parametric model은 종종 존재하는 이미지 혹은 이미지의 패치를 데이터베이스로부터 matching을 하며

 

texture synthesis, super-resolution, in-painting과 같은 분야에서 사용되어 왔다.

 

 

이미지를 생성하기 위한 parametric model은 MNIST나 texture synthesis를 위해 광범위하게 연구되어 왔다.

 

하지만, 현실 세계의 자연스러운 이미지를 만들어내는 것은 최근까지 큰 성공을 거두지 못했다.

 

이미지를 생성하기 위한 variational sampling approach는 어느 정도의 성공을 거두었으나, 샘플들이 종종 흐릿해지는 현상이 나타난다. (VAE를 생각하시면 됩니다..! VAE에 대한 설명과 코드는 이전에 다루었기 때문에, 궁금하신 분들은 찾아보시면 될 것 같아요!)

 

다른 접근법은 iterative forward diffusion process를 사용하여 이미지를 만들어낸다.

 

Generative Adversarial Networks가 생성한 이미지도 noisy 하고 이해할 수 없는 현상이 나타난다.

 

parametric 접근법에 대한 laplacian pyramid extension은 더 높은 퀄리티의 이미지를 보여주지만, 여전히 여러 모델의 chaining에 의해 유입된 noise에 의해서 물체가 흔들리게 보이는 현상이 나타난다.

 

Recurrent network approach와 deconvolution network approach는 최근에 자연스러운 이미지를 만드는 것에 있어서 어느 정도의 성공을 거두었으나, 그들은 supervised tasks를 위해 generator를 활용하지 않았다. (deconvolution network approach에서 generator를 사용하지 않았기 때문에 해당 연구와의 차별점?으로 적은 게 아닐까 싶네요.)

 

 

 

2.3 Visualizing the internal of CNNs

 

 

신경망을 사용하는 것에 있어서 끊임없는 비평 중 하나는 신경망이 black-box 방법이라는 것이며 인간이 사용할 수 있는 간단한 알고리즘의 형태로 네트워크가 무엇을 하는지에 대해 거의 이해하지 못하고 있다는 것이다.

 

CNN의 맥락에서, Zeiler et. al.은 deconvolution과 filtering the maximal activation을 사용하여 네트워크에서 각 convolution filer의 대략적인 목적을 확인할 수 있었다.

 

마찬가지로, 입력에 gradient descent를 사용하여 필터의 특정한 subset을 활성화하는 이상적인 이미지를 확인할 수 있다.

 

 

 

3. Approach and model architecture

 

 

CNN을 사용해서 이미지를 모델링하기 위해 GANs를 확장하려는 과거의 시도는 성공적이지 못했다.

 

이는 LAPGAN의 저자들이 보다 신뢰성 있게 모델링할 수 있는 저해상도 생성 이미지를 반복적으로 상향 조정하는 alternative approach를 개발하도록 동기 부여했다.

 

또한 우리는 supervised literature에서 흔하게 사용되는 CNN 아키텍처를 사용해 GAN을 스케일링하려는 시도에서 어려움들을 마주했다.

 

하지만, 광범위한 모델 탐구 후에 우리는 많은 데이터셋에 대해서 안정적인 학습을 가져오는 아키텍처의 family를 확인하였으며 이는 더 높은 해상도와 더 깊은 생성 모델이 가능하도록 만들었다. (family를 어떻게 번역해야 할지 애매해서 그냥 뒀습니다. 사실상 다양한 모델 아키텍처를 시도해보면서 가장 적합한 형태의 모델 아키텍처를 찾았다는 의미인 것 같네요.)

 

우리 접근법의 핵심은 CNN 아키텍처에 대한 3개의 최근 검증된 변화를 채택하고 수정하는 것이다.

 

 

첫 번째는 max-pooling과 같은 deterministic spatial pooling functions를 stride convolution으로 대체하는 모든 convolutional net은 네트워크가 이것 자체의 spatial downsampling을 학습하도록 허용한다는 것이다.

 

우리는 이 접근법을 generator에서 사용하였으며, 이는 우리의 spatial upsampling을 학습하도록 만들어줬고 discriminator에서도 사용한다.

 

(max pooling은 deterministic 하게, 즉 결정론적으로 공간적인 풀링을 진행하지만, convolution에 stride를 하도록 만들면 자연스럽게 공간적인 정보를 down sampling 하도록 학습을 할 수 있기 때문에 이렇게 하겠다는 의미입니다. 뒤에서 나오겠지만, DCGAN은 max pooling을 사용하지 않고 stride를 통해서 해상도를 줄이는 제약을 가지고 있습니다.)

 

 

두 번째는 마지막 convolutional features에서 fully connected layer를 제거하는 쪽으로의 트렌드이다. 

 

이것에 대한 가장 강력한 예시는 State of The Art (성능이 가장 좋다는 말) 이미지 분류 모델에서 활용되어 온 global average pooling이다. 

 

우리는 global average pooling이 모델의 안정성을 증가시키지만 수렴 속도를 해친다는 사실을 알게 되었다.

 

가장 높은 convolutional feature를 generator와 discriminator의 input와 output 각각에 직접적으로 연결하는 타협안은 잘 작동했다. (직접적으로 연결한다는 의미가, pooling을 쓰지 않고 convolution 연산 만으로 input부터 output까지 연결한다는 의미인 것 같습니다.)

 

Uniform noise distribution $Z$를 input으로 받는 GAN의 첫 번째 layer는 단순히 행렬 곱이기 때문에 fully connected라고 불릴 수 있지만, 결과는 4차원 tensor로 reshape 되고 convolution stack의 출발지점으로 사용된다. 

 

(해당 내용은 모델 아키텍처에서 이 부분을 이야기하는 것으로 보입니다.)

 

Discriminator에서는, 마지막 conv layer는 flatten 되고 하나의 sigmoid output으로 들어간다. 모델 아키텍처의 한 예시를 시각화한 것이 Fig. 1에 나와있다.

 

 

 

세 번째는 각 unit에 들어가는 input이 평균이 0이고 분산이 1이 되도록 normalize 해주는 것을 통해 학습을 안정적으로 만들어주는 Batch Normalization이다. 

 

이는 안 좋은 초기화 때문에 발생하는 학습 문제를 해결하고 더 깊은 모델에서 gradient 흐름을 도와준다.

 

이는 deep generator가 학습을 시작할 때 모든 샘플들이 GANs에서 발견되는 일반적인 failure mode인 하나의 point로 collapse 되는 것을 방지한다. (GAN의 학습 초기에 같은 모양만 생성하는 현상을 이야기하는 것 같습니다.)

 

하지만, 모든 layer에 직접적으로 batch norm을 적용하는 것은 sample oscillation과 모델 불안정성을 야기한다.

 

이는 generator의 output layer와 discriminator의 input layer에 batchnorm을 적용하지 않는 것을 통해 피할 수 있다.

 

 

 

ReLU activation은 Tanh function을 사용하는 output layer만 빼고 generator의 모든 layer에서 사용된다.

 

우리는 bounded activation을 사용하는 것이 모델로 하여금 더 빠르게 saturate 하도록 학습시키고 학습 분포의 color space를 포괄하도록 학습함을 발견했다. 

 

우리는 Discriminator 내에서 leaky rectified activation이 잘 작동함을 확인하였고, 특히 높은 resolution modeling에서 그러하다. (leaky rectified activation은 보통 LeakyReLU라고 부르는 활성화 함수인데, ReLU는 $x < 0$ 구간에서는 0이고 $x >=0$에서는 $x$의 값을 가지지만, LeakyReLU는 $x < 0$ 구간에서는 $ax$이고, $x >= 0$ 구간에서는 $x$입니다.)

 

이는 maxout activation을 사용한 original GAN paper와는 대조적이다. 

 

 

안정적인 DCGAN을 위한 아키텍처 가이드라인

 

• Pooling layer를 strided convolution (discriminator)와 fractional-strided convolution (generator)로 교체한다.
• Generator와 discriminator 모두에서 Batch Norm을 사용한다.
• 더 깊은 아키텍처를 위해 fully connected hidden layer를 제거한다.
• Generator에서 Tanh를 사용하는 output layer를 제외한 모든 layer에서 ReLU activation을 사용한다.
• Discriminator의 모든 layer에서 LeakyReLU activation을 사용한다.

 

 

 

4. Details of adversarial training

 

 

우리는 DCGANs를 Large-scale Scene Understanding (LSUN), Imagenet-1k, 새롭게 모은 Face dataset의 총 3개의 데이터셋에 학습했다. 각 데이터셋의 사용에 대한 세부사항은 아래에 나와있다.

 

학습 이미지에 대해서는 tanh activation function의 범위인 [-1, 1]에 맞추기 위한 스케일링을 제외하고는 어떤 전처리도 적용되지 않았다. 

 

모든 모델은 mini-batch stochastic gradient descent (SGD)를 이용해서 학습되었으며, 128 사이즈의 mini-batch를 사용했다.

 

모든 weight는 standard deviation 0.02를 가지는 zero-centered normal distribution을 이용하여 초기화되었다.

 

LeakyReLU에서는, leak의 slope는 모든 모델에서 0.2로 고정한다.

 

이전 GAN 연구들은 학습을 가속화하기 위해서 momentum을 사용하였으나, 우리는 튜닝된 hyperparameters를 가지고 Adam optimizer를 사용했다.

 

우리는 0.001의 learning rate가 너무 높다고 판단해 0.0002를 사용했다.

 

추가적으로, momentum term $\beta_1$을 제안된 값 0.9가 training oscillation과 불안정을 야기하여 학습을 안정화시키고자 0.5로 줄였다.

 

 

 

4.1부터 4.3 까지는 개별 데이터셋의 적용 내용이므로, 생략합니다.

 

 

 

5. Empirical validation of DCGANs capabilities

 

5.1 Classifying CIFAR-10 using GANs as a feature extractor

 

 

unsupervised representation learning algorithm의 품질을 평가하는 하나의 방법은 supervised dataset에 이를 feature extractor로 적용해보는 것이며 이 feature의 top에 linear model을 fitting 시켜서 성능을 평가하는 것이다.

 

CIFAR-10 dataset에 대해서, feature learning algorithm으로 K-means를 활용하는 single layer feature extraction pipeline으로부터 매우 강력한 baseline performance가 검증되어 왔다.

 

매우 많은 양의 feature maps (4800)을 사용했을 때, 이 방법은 80.6% accuracy를 달성했다.

 

이 방법을 unsupervised multi-layered로 확장하면 82.0% accuracy를 달성했다.

 

Supervised tasks를 위해 DCGANs에 의해서 학습된 representation의 품질을 평가하기 위해 DCGAN을 Imagenet-1k에 학습하고 discriminator의 모든 layer에서 나온 convolutional feature를 사용하였으며 4x4 spatial grid를 만들기 위해서 각 layer의 representation을 max-pooling 했다.

 

이 feature들을 flatten 하고 이를 concatenate 해서 28672차원의 벡터를 만든 다음 이에 대해서 regularized linear L2-SVM classifier를 학습시킨다.

 

이는 82.8% accuracy를 달성했으며, 모든 K-means 기반 접근법보다 더 좋은 성능을 달성했다.

 

특히 discriminator는 K-means 기반의 기법과 비교했을 때 훨씬 적은 feature map을 가지지만 (가장 높은 layer에서 512개) 4x4 spatial locations의 많은 layer 때문에 더 큰 전체 feature vector size를 갖게 된다.

 

추가적으로, 우리의 DCGAN은 CIFAR-10에 학습이 되지 않았으며, 이 실험은 또한 학습된 feature의 domain robustness를 증명했다. 

 

(Table 1에서는 기존의 K-means와 같은 unsupervised 방법론에 비해서 훨씬 더 좋은 accuracy를 보임을 나타내고 있습니다. 이를 통해, DCGAN이 학습한 unsupervised representation의 품질이 좋음을 알 수 있습니다.)

 

 

5.2는 SVHN 데이터에 실행한 결과라서, 생략하겠습니다.

 

 

6. Investigating and visualizing the internals of the networks

 

 

우리는 학습된 generator와 discriminator를 다양한 방식으로 살펴볼 것이다. 우리는 training set에 대해서 어떠한 종류의 nearest neighbor search를 하지 않았다.

 

pixel이나 feature space에서의 nearest neighbor는 작은 이미지 변환에 의해서 하찮게 속게 된다.

 

우리는 또한 모델을 정량적으로 평가하기 위해서 log-likelihood metrics를 사용하지 않았으며, 이는 안 좋은 metric이기 때문이다.

 

 

6.1. Walking in the latent space

 

 

우리가 한 첫 번째 실험은 latent space의 landscape를 이해하는 것이다. 학습된 manifold에서 걷는 것은 일반적으로 우리에게 memorization의 signs에 대해서 말해줄 수 있고 (만약 sharp transitions이 있는 경우) 공간이 계층적으로 collapsed 된 방법에 대해서도 말해줄 수 있다.

(latent space에서 값을 점차적으로 변화함에 따라서, 이미지가 확 바뀌게 되면 이는 training sample을 학습했다기보다는 그저 기억한다고 볼 수 있습니다. 그 부분을 memorization의 sign이라고 표현한 것으로 보입니다. )

 

만약 latent space에서 걷는 것이 이미지 생성에 대해서 의미론적인 변화를 야기하는 경우(객체가 추가되거나 제거되는 것을 의미) 우리는 모델이 관련되어 있는 표현을 학습했고 흥미로운 표현을 학습했다고 추론할 수 있다. 

 

결과는 Fig. 4에서 확인할 수 있다.

 

 

 

 

6.2 Visualizing the discriminator features

 

 

 

이전 연구는 큰 이미지 데이터셋에 CNN을 supervised training 했을 때 매우 강력한 학습된 feature를 야기한다는 사실을 보였다.

 

추가적으로, scene classification에 학습된 supervised CNN은 object detectors를 학습한다.

 

우리는 large image dataset에 학습된 unsupervised DCGAN도 역시 흥미로운 특징의 계층을 학습할 수 있음을 보인다.

 

Springenberg et al. 에 의해 제안된 guided backpropagation을 사용해서, Fig.5에서 discriminator에 의해서 학습된 feature가 침대나 창문과 같은 bedroom의 특정한 부분에서 활성화된다는 것을 보였다.

 

비교를 위해서, 같은 이미지에서, 우리는 의미론적으로 관련이 있거나 흥미로운 어떤 것에 활성화되지 않은 임의로 초기화된 feature에 대한 baseline을 제공한다.

 

(guided backpropagation을 정확히 해당 논문에서 설명하지 않고 있어서, 저도 정확히는 알 수 없지만 discriminator가 진짜라고 판별하는 데 있어서 가장 크게 기여한 부분을 표현한 이미지가 아닐까 라는 생각이 듭니다.)

 

 

 

6.3 Manipulating the generator representation

 

 

6.3.1 forgetting to draw certain objects

 

 

Discriminator에 의해서 학습된 표현에 더하여, generator가 학습한 표현이 무엇인지에 대한 질문이 있다.

 

샘플의 품질은 generator가 베개, 창문, 램프, 문, 그리고 이것저것 다양한 가구와 같은 주요한 장면 요소에 대한 구체적인 object representation을 학습했음을 시사한다.

 

이러한 표현들이 취하는 형태를 탐구하기 위해, 우리는 generator에서 창문을 완전히 제거하려고 실험을 수행했다.

 

 

150개 sample에 대해서, 52개의 창문 bounding box를 직접 그렸다.

 

두 번째로 높은 convolution layer feature에 대해서, logistic regression은 bounding box 안쪽에 있는 activation은 positive로, 같은 이미지에서 랜덤한 샘플을 뽑아서 negative로 지정하는 기준을 사용해 feature activation이 window에 있는지 없는지를 예측하기 위해 fitting 되었다.

 

이 간단한 모델을 사용하면, 0보다 큰 weight를 가지는 모든 feature map이(총 200개) 모든 spatial location으로부터 떨어져 나간다. 

 

그러고 나서, 임의의 새로운 샘플은 feature map removal을 가지고 만들어지고, 없이 만들어진다.

 

(솔직히 이 내용만 봐서는 정확히 어떻게 만들었는지가 와 닿지는 않은데, 특히 weight가 0보다 큰 경우에 해당 activation을 어떻게 처리하는지? 이 부분이 살짝 모호한 느낌이네요.)

 

 

Window dropout을 가지고 만들어진 이미지와 없이 만들어진 이미지는 Fig. 6에 나와있다.

 

그리고 흥미롭게도, 네트워크는 대개 bedroom에 window를 그리는 것을 까먹고, 이를 다른 object로 대체했다.

 

 

6.3.2 Vector arithmetic on face samples

 

 

단어의 학습된 학습된 representation을 평가하는 맥락에서 (Mikolov etal., 2013) 단순한 산술 연산이 representation space에서 풍부한 linear structure를 나타낸다는 것이 검증되었다.

 

하나의 표준이 되는 예시는 vector("King") - vector("Man") + vector("Woman")이 Queen을 의미하는 vector에 가장 가까운 vector를 야기한다는 사실을 나타낸다.

 

우리는 유사한 구조가 우리의 generator의 $Z$ representation에서 나타나는지 아닌지를 살펴보았다.

 

우리는 시각적 개념에 대한 예시 샘플 세트의 $Z$ 벡터에 대해 유사한 산수를 수행했다.

 

개념 당 오직 하나의 샘플로 실험을 진행하는 것은 불안정했으나, 3개의 예시에 대한 $Z$ vector를 평균 내는 것은 의미론적으로 산수를 따르는 안정적이고 일관된 생성을 보여주었다.

 

Fig. 7에 나타난 object manipulation에 더해서, 우리는 face pose 또한 $Z$ space에서 선형적으로 모델링 될 수 있음을 검증하였다. (Fig. 8)

 

 

 

이러한 검증은 우리 모델에 의해서 학습된 $Z$ representation을 사용하여 흥미로운 application이 개발될 수 있음을 제안한다.

 

Conditional generative model이 scale, rotation, position과 같은 object attribute를 설득력 있게 모델링하는 방법을 학습할 수 있음은 이전에 증명되었다. (Dosovitskiy et al., 2014)

 

이는 우리가 알기로는 완전히 unsupervised models에서 이러한 현상이 발생한다는 것을 증명한 첫 번째 사례이다.

 

위에서 언급된 벡터 산수를 더 탐구하고 개발하는 것은 복잡한 이미지 분포의 conditional generative modeling에 필요한 데이터의 양을 극적으로 줄일 수 있다.

 

 

7. Conclusion and future work

 

 

우리는 generative adversarial networks를 학습시키는 더욱 안정적인 아키텍처 set을 제안하였으며 adversarial networks가 generative modeling과 supervised learning을 위한 good image representation을 학습한다는 것에 대한 증거를 제시했다.

 

여전히 모델 불안정성의 몇 가지 형태가 남아 있으며 우리는 모델이 더 오래 학습할수록 그들이 때때로 filter의 subset을 하나의 oscillating mode로 붕괴된다는 것을 알고 있다.

 

이후 연구는 이런 불안정성의 형태를 다룰 필요가 있다.

 

우리는 이 framework를 video (frame prediction을 위한)나 audio (speech synthesis를 위한 pre-trained feature)와 같은 다른 분야로 확장하는 것이 매우 흥미로울 것이라고 생각한다.

 

학습된 latent space에 대한 특성을 더욱 조사해보는 것은 또한 흥미로울 것이다.

 

 

 

여기까지 DCGAN 논문에 대한 내용들을 쭉 다뤄보았는데요.

 

이전에 GAN을 이용해서 MNIST를 만들어본 적이 있지만, 아무래도 엄청 간단한 모델이고 하다보니 숫자처럼 보이는 샘플들이 나오기는 했으나 그렇게까지 좋은 샘플이 나오지는 못했습니다.

 

아마도 DCGAN을 활용하면 조금 더 진짜 같은 이미지가 나오지 않을까? 하는 기대를 해보면서 다음 글에서는 code review로 찾아오겠습니다.

 

 

 

이번 글에서는 지난 글에서 review한 AAE 논문을 코드로 구현한 내용을 살펴보겠습니다.

 

 

AAE 논문의 paper review : cumulu-s.tistory.com/26

 

3. Adversarial Autoencoders(AAE) - paper review

오늘은 Autoencoder의 구조와 GAN framework를 결합해 탄생한 AAE에 대해서 알아보도록 하겠습니다. paper : arxiv.org/abs/1511.05644 Adversarial Autoencoders In this paper, we propose the "adversarial aut..

cumulu-s.tistory.com

 

AAE 논문에서는, AAE를 활용할 수 있는 다양한 applications을 제시하였는데 일단 저는 가장 기초적인 AAE를 짜봤습니다.

 

 

hyperparameter도 바꿔보면서, 수십번의 시도를 하였음에도 논문에서 나온대로 Encoder가 manifold learning을 하지 못해서 코드가 완벽하다고 하기는 어려울 것 같습니다. (GAN에서 discriminator와 generator가 적절한 수준에서 학습시키기가 어려운 것 때문으로 추측하고 있습니다. 이럴땐 공식 코드가 있고 없고의 차이가 크다고 느껴지네요 ㅠㅠ)

 

 

대략 이런식으로 코드를 짜보면 되겠구나 정도로 참고해주시면 되겠습니다.

 

 

import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision.datasets as dsets
import torchvision.transforms as transforms
from torch.autograd import Variable
from torch.utils.tensorboard import SummaryWriter
import datetime
import os
import torchvision
import itertools
import numpy as np
from math import sin,cos,sqrt

먼저 필요한 package들을 import 해줍니다.

 

 

current_time = datetime.datetime.now() + datetime.timedelta(hours= 9)
current_time = current_time.strftime('%Y-%m-%d-%H:%M')

saved_loc = os.path.join('/content/drive/MyDrive/AAE_Result', current_time)
os.mkdir(saved_loc)

print("저장 위치: ", saved_loc)

writer = SummaryWriter(saved_loc)

 

이 부분은 이전 코드 리뷰에서도 이미 다뤘던 부분이라서, 넘어가도록 하겠습니다.

 

직접 돌리실 때는 경로를 원하시는 위치로 바꿔주시면 됩니다.

 

 

# MNIST Dataset 
dataset = dsets.MNIST(root='/content/drive/MyDrive/MNIST', 
                      train=True, 
                      transform=transforms.ToTensor(),  
                      download=True)

# Data Loader (Input Pipeline)
data_loader = torch.utils.data.DataLoader(dataset=dataset, 
                                          batch_size=200, 
                                          shuffle=True)

testset = dsets.MNIST(root='/content/drive/MyDrive/MNIST', 
                      train=False, 
                      transform=transforms.ToTensor(),  
                      download=True)

testloader = torch.utils.data.DataLoader(dataset=testset,
                                         batch_size = 200,
                                         shuffle = True)

사용할 데이터셋인 MNIST를 불러와줍니다.

 

 

 

def to_var(x):
    if torch.cuda.is_available():
        x = x.cuda()
    return Variable(x) 

이 함수는, x 라는 변수를 GPU 사용이 가능할 때, cuda로 옮겨주고 이를 Variable로 만들어주는 코드입니다.

 

 

#Encoder
class Q_net(nn.Module):  
    def __init__(self,X_dim,N,z_dim):
        super(Q_net, self).__init__()
        self.lin1 = nn.Linear(X_dim, N)
        self.lin2 = nn.Linear(N, N)
        self.lin3gauss = nn.Linear(N, z_dim)

        self.lin1.weight.data.normal_(0, 0.01)
        self.lin2.weight.data.normal_(0, 0.01)
        self.lin3gauss.weight.data.normal_(0, 0.01)
    def forward(self, x):
        x = F.dropout(self.lin1(x), p=0.25, training=self.training)
        x = F.relu(x)
        x = F.dropout(self.lin2(x), p=0.25, training=self.training)
        x = F.relu(x)
        xgauss = self.lin3gauss(x)
        return xgauss

다음으로는 Encoder 부분입니다. X_dim은 이미지의 사이즈가 될 것이고, N은 중간 hidden layer의 node 수 입니다. z_dim는 latent space의 차원이구요.

 

논문의 Appendix A에서 'The weights are initialized with a Gaussian distribution with the standard deviation of 0.01.'라고 적혀 있으므로, weight.data.normal_(0, 0.01)을 이용해서 초기화를 해줍니다.

 

그리고 'The activation of the last lyaer of $q(z|x)$ is linear'라고 적혀 있으므로, 마지막 layer에는 activation function을 따로 만들지 않습니다.

 

# Decoder
class P_net(nn.Module):  
    def __init__(self,X_dim,N,z_dim):
        super(P_net, self).__init__()
        self.lin1 = nn.Linear(z_dim, N)
        self.lin2 = nn.Linear(N, N)
        self.lin3 = nn.Linear(N, X_dim)

        self.lin1.weight.data.normal_(0, 0.01)
        self.lin2.weight.data.normal_(0, 0.01)
        self.lin3.weight.data.normal_(0, 0.01)

    def forward(self, x):
        x = F.dropout(self.lin1(x), p=0.25, training=self.training)
        x = F.relu(x)
        x = F.dropout(self.lin2(x), p=0.25, training=self.training)
        x = F.relu(x)
        x = self.lin3(x)
        return torch.sigmoid(x)

 

다음은 Decoder 입니다. Decoder도 동일하게 weight 초기화를 적용해주고, 이번에는 마지막 layer의 결과가 이미지와 동일하게 0부터 1사이의 값이 나와야하므로 sigmoid를 마지막에 적용해줍니다.

 

 

# Discriminator
class D_net_gauss(nn.Module):  
    def __init__(self,N,z_dim):
        super(D_net_gauss, self).__init__()
        self.lin1 = nn.Linear(z_dim, N)
        self.lin2 = nn.Linear(N, N)
        self.lin3 = nn.Linear(N, 1)

        self.lin1.weight.data.normal_(0, 0.01)
        self.lin2.weight.data.normal_(0, 0.01)
        self.lin3.weight.data.normal_(0, 0.01)
    def forward(self, x):
        x = F.dropout(self.lin1(x), p=0.2, training=self.training)
        x = F.relu(x)
        x = F.dropout(self.lin2(x), p=0.2, training=self.training)
        x = F.relu(x)
        return torch.sigmoid(self.lin3(x))  

 

다음 코드는 Discriminator입니다. latent vector를 입력으로 받아, 해당 latent vector가 진짜인지 가짜인지 판별하는 역할을 하죠. 

 

 

 

EPS = 1e-15
z_red_dims = 2
Q = Q_net(784,1000,z_red_dims).cuda()
P = P_net(784,1000,z_red_dims).cuda()
D_gauss = D_net_gauss(1000,z_red_dims).cuda()

EPS는 매우 작은 숫자로 설정되어 있고, latent dimension은 2로 설정했습니다.

 

그리고 논문의 Appendix A에 'The encoder, decoder and discriminator each have two layers of 1000 hidden units with ReLU activation function'으로 적혀 있으므로, hidden layer의 node는 1000개로 지정하였습니다.

 

 

# Set learning rates
gen_lr = 0.0001
reg_lr = 0.00005

# encode/decode optimizers
optim_P = torch.optim.Adam(P.parameters(), lr=gen_lr)
optim_Q_enc = torch.optim.Adam(Q.parameters(), lr=gen_lr)
# regularizing optimizers
optim_Q_gen = torch.optim.Adam(Q.parameters(), lr=reg_lr) 
optim_D = torch.optim.Adam(D_gauss.parameters(), lr=reg_lr)
    
data_iter = iter(data_loader)
iter_per_epoch = len(data_loader)
total_step = 60000 

Reconstruction error를 최소화하는 상황에서 Encoder와 Decoder는 0.0001의 learning rate를 가지고 학습하도록 설계하였으며, Regularization error를 최소화하는 상황에서 Discriminator와 generator는 0.00005의 learning rate를 가지고 학습하도록 설계하였습니다.

 

data_iter라는 이름으로 data_loader를 iterator로 만들어주고, 전체 training step은 6만번 진행합니다. (batch size가 100개라서, 600번 진행하면 1 epoch이며, 6만번 진행하면 100 epoch이 됩니다.)

 

iter_per_epoch는 600이 나옵니다.

 

 

for step in range(total_step):

    # Reset the data_iter
    if (step+1) % iter_per_epoch == 0:
        data_iter = iter(data_loader)

    # Fetch the images and labels and convert them to variables
    images, labels = next(data_iter)
    images, labels = to_var(images.view(images.size(0), -1)), to_var(labels)

 

다음으로는 반복문 부분을 보겠습니다.

 

앞에서 iterator를 정의했었는데, 만약 600번(1 에폭)이 지나면 새롭게 다시 iterator를 reset 해줍니다.

 

그리고 iterator는 next()라는 명령어를 통해서 한개씩 데이터를 빼낼 수 있기 때문에 next(data_iter)를 적용해줍니다.

 

next를 통해서 빼넨 이미지는 (100, 1, 28, 28)의 형태를 가지고 있는데 앞에서 정의한 Encoder는 (Batch_size, 28*28)의 형태를 input으로 받습니다. 따라서, images.view(images.size(0), -1)를 통해서 (100, 784) 사이즈로 맞춰줍니다.

 

딥러닝에서는 항상 shape가 매우 중요하니까, 코드를 보실 때 이런 부분을 염두에 두시고 보시는게 좋다고 생각합니다.

 

 

    # ======================================== #
    # =====Phase 1 : Reconstruction Loss====== #
    # ======================================== #
    
    P.zero_grad()
    Q.zero_grad()
    D_gauss.zero_grad()

    z_sample = Q(images)   #encode to z
    X_sample = P(z_sample) #decode to X reconstruction
    recon_loss = F.binary_cross_entropy(X_sample+EPS, images+EPS, reduction = 'sum')

    writer.add_scalar("Train/Reconstruction_loss", recon_loss.item() / len(images), step)

    recon_loss.backward()
    optim_P.step()
    optim_Q_enc.step()

다음으로는 Loss를 계산하고, backprop 시켜보겠습니다.

 

먼저, Encoder와 Decoder, Discriminator를 모두 zero_grad() 해줍니다.

 

z_sample은 이미지를 latent vector로 바꾼 것을 저장한 것이고, X_sample은 latent vector를 이용해 이미지를 복원한 결과입니다.

 

그리고 recon_loss는 X_sample과 원래 이미지를 binary_cross_entropy를 이용해서 loss 값을 계산해줍니다.

 

writer.add_scalar는 reconstruction loss 값을 tensorboard에 write하는 코드구요.

 

계산된 recon_loss에 대해서 .backward()를 해주면 loss에 대한 각 변수들의 gradient가 계산됩니다. 

 

그리고 나서 optim.step()을 통해서 optimizer에 지정된 모델의 매개변수들을 계산된 gradient를 가지고 업데이트 해줍니다.

 

 

    # ======================================== #
    # =====Phase 2 : Discriminator Loss======= #
    # ======================================== #

    Q.eval()
    z_real_gauss = Variable(torch.randn(images.size()[0], z_red_dims) * 5.).cuda()
    D_real_gauss = D_gauss(z_real_gauss)

    z_fake_gauss = Q(images)
    D_fake_gauss = D_gauss(z_fake_gauss)

    D_loss = -torch.mean(torch.log(D_real_gauss + EPS) + torch.log(1 - D_fake_gauss + EPS))

    writer.add_scalar("Train/Discriminator_loss", D_loss.item() / len(images), step)

    D_loss.backward()
    optim_D.step()

 

다음 단계는 Discriminator loss를 계산하고, 업데이트 하는 코드입니다.

 

먼저, Q(Encoder)를 추론 모드로 전환해줍니다. (Q.eval()을 하면 해당 모델의 파라미터가 업데이트 되지 않습니다.)

 

z_real_gauss라는 이름으로 평균이 0이고 표준편차가 5인 가우시안 분포에서 임의의 값들을 만들어냅니다.

 

torch.randn(images.size()[0], z_red_dims)를 이용하면 평균이 0이고 표준편차가 1짜리인 (100, 2) shape를 가지는 값들을 만들게 되는데, 여기에 5.를 곱해서 표준편차가 5가 되도록 만든 코드라고 보시면 됩니다.

 

이 가우시안 분포 값을 Discriminator에 넣어서 나온 결과를 D_real_gauss로 저장합니다. 

 

다음으로는 우리가 가지고 있는 training image를 Encoder에 넣어서 나온 결과를 z_fake_gauss로 저장하고, 이를 Discriminator에 넣어서 나온 결과를 D_fake_gauss로 저장합니다. 

 

그리고나서, GAN의 Discriminator loss 계산 방법을 그대로 적용하여 D_loss를 계산해줍니다. 

 

참고로, 여기서 EPS를 각각 더해주는데, 궁금해서 이걸 빼보니까 에러가 나더라고요. 확실하진 않은데 이미지가 모두 0이여 버리면 gradient 연산을 해줄 때 문제가 발생하나봅니다. 그래서 엄청나게 작은 양수를 넣어줘서 그런 연산 이슈를 해결하려고 EPS라는 값을 넣어주는 것 같습니다. 1e-15면 엄청나게 작은 값이라서 실제 연산 결과에는 영향을 미치지 않을 정도죠.

 

이번 코드에서는 Discriminator만 학습을 시켜주면 되기 때문에 D_loss.backward()를 해주고 optim_D.step()을 해줍니다.

 

 

 

    # ======================================== #
    # =======Phase 3 : Generator Loss========= #
    # ======================================== #

    Q.train()

    z_fake_gauss = Q(images)
    D_fake_gauss = D_gauss(z_fake_gauss)
    
    G_loss = - torch.mean(torch.log(D_fake_gauss + EPS))

    G_loss.backward()
    optim_Q_gen.step()

    writer.add_scalar("Train/Generator_loss", G_loss.item() / len(images), step)

마지막으로 Generator loss를 계산해봅니다.

 

이번에는 encoder이자 generator인 Q를 학습해야 하므로, Q.train()으로 학습 모드를 만들어줍니다.

 

그리고 training image를 encoder에 넣어서 latent vector로 만들어주고, 이를 Discriminator에 넣어서 계산해줍니다.

 

GAN에서 얘기한 Generator loss를 동일하게 적용해주면 완성이 됩니다.

 

 

 if (step+1) % 100 == 0:
        print('Step [%d/%d], Recon_Loss: %.4f, D_loss: %.4f, G_loss: %.4f' 
              %(step+1, total_step, recon_loss.item() / len(images), D_loss.item() / len(images), G_loss.item() / len(images)))

학습이 잘 되고 있는지 확인해야 하니까, step 100번마다 reconstruction loss와 discriminator loss, generator loss가 찍히도록 짰습니다.

 

 

 

if (step+1) % 300 == 0:

        # Test the model's ability to reconstruct test set image. 
        
        Q.eval()
        P.eval()

        sample, _ = next(iter(testloader))

        sample = to_var(sample.view(sample.size(0), -1)) # (100, 784)

        z_ = Q(sample) # (100, 120)
        recon_ = P(z_) # (100, 784)

        n = min(sample.size(0), 8)
        comparison = torch.cat([sample.view(100, 1, 28, 28)[:n], recon_.view(100, 1, 28, 28)[:n]])
        grid = torchvision.utils.make_grid(comparison.cpu())
        writer.add_image("Test image - Above: Real data, below: reconstruction data", grid, (step+1)/300 )
        
        # Test the model's ability to decode latent variable to image data
        
        z_test = Variable(torch.randn(16, z_red_dims) * 5.).cuda()
        recon_image = P(z_test).cpu()
        grid = torchvision.utils.make_grid(recon_image.view(16, 1, 28, 28))
        writer.add_image("Latent to Image", grid, (step+1)/300 )

그리고 300번마다 제대로 잘 학습하고 있는지를 파악하기 위해서 다음과 같은 코드를 짰습니다.

 

먼저, Encoder와 Decoder는 inference mode로 바꿔주고, testloader에서 샘플을 받아옵니다.

 

즉, 모델이 아직 본적 없는 이미지들에 대해서 시험을 해보는 것이죠.

 

학습된 Q(Encoder)에 test 이미지를 넣어서 latent vector로 만들어줍니다. 이를 z_로 저장해주고요.

 

그리고 이 z_를 가지고 Decoder에 집어 넣어서 원래 이미지를 복원해줍니다. 이를 recon_으로 저장해줍니다.

 

다음으로는 원래 기존 test image 중에서 8개, 그리고 복원된 이미지 중에서 8개를 가져온 다음 이를 torch.cat을 통해서 concat 해줍니다. sample.view(100, 1, 28, 28)[:n]를 하면 (8, 1, 28, 28)가 될 것이고, recon_.view도 마찬가지로 (8, 1, 28, 28)가 됩니다.

 

여기에 torch.cat을 사용해주면 (16, 1, 28, 28)짜리 이미지가 만들어질 것이고, 이를 torchvision의 make_grid를 통해서 그리드 이미지로 만들어줍니다. 이 때, comparison은 모두 cuda에 올라가 있으므로, cpu()를 통해서 다시 cpu쪽으로 이동시켜줍니다. (GPU를 활용한 cuda 연산을 할 때는 값들이 cuda에 올라가 있는지 cpu에 있는지를 잘 확인해야 합니다.)

 

이를 writer.add_image를 통해서 tensorboard레 써줍니다.

 

그리고 z_test라는 이름으로 평균이 0이고 표준편차가 5짜리로 (16, 2) 차원의 랜덤한 값들을 만들어주고,

 

이를 Decoder에 넣어서 복원해줍니다. recon_image라고 저장해뒀죠.

 

그리고 이를 (16, 1, 28, 28)로 shape를 변경하고, 다시 한번 make_grid를 이용해서 그리드 이미지로 만들어줍니다.

 

이를 tensorboard에 똑같이 저장해주죠.

 

 

해당 코드를 통해서 보고자 하는 것은 다음과 같습니다.

 

1) 모델이 내가 본 적 없는 테스트 이미지를 이미지 => Encoder => Decoder => 복원 과정을 거치면서 제대로 복원 시킬 수 있는 능력을 갖추고 있는가?

 

2) 임의의 $N(0, 5)$를 따르는 값들을 만들어서 Decoder에 투입하였을 때, 적절한 형태의 이미지를 만들어낼 수 있는가? 

 

 

# save the Model
torch.save(Q.state_dict(), os.path.join(saved_loc, 'Q_encoder_weights.pt'))
torch.save(P.state_dict(), os.path.join(saved_loc, 'P_weights.pt'))
torch.save(D_gauss.state_dict(), os.path.join(saved_loc, 'D_weights.pt'))

마지막은 그냥 모델 weight 저장하는 코드니까, 별도의 설명 없이 넘어가겠습니다. 

 

 

여기까지가 코드이고, 다음으로는 결과를 보여드리겠습니다.

 

 

 

Train 과정에서의 Reconstruction error와 Discriminator loss, Generator loss입니다.

 

Reconstruction error는 계속해서 줄어들고 있는 모습을 보이고 있구요.

 

Discriminator loss는 우상향, Generator loss는 우하향 하고 있는 모습을 보이고 있습니다.

 

Generator loss가 $-log(D(G(z)))$ 임을 감안한다면, 이것이 감소한다는 의미는 $log(D(G(z)))$가 증가한다는 의미이고

 

Log 그래프를 생각해보시면, 이것이 증가한다는 의미는 Discriminator가 $G(z)$를 더욱 진짜라고 판단한다 라고 볼 수 있습니다.

 

 

다음으로는, Test를 보겠습니다.

 

아까 위에서 설명드린대로, 이는 (16, 2) 차원의 Gaussian random vector를 가지고 Decoder를 이용해 복원한 결과입니다.

 

완전 초창기 결과라서 성능이 매우 좋지 않음을 확인할 수 있습니다.

 

 

 

다음은 100 epoch, 즉 step 60000일 때(학습 완료)의 결과입니다. 아까보다는 조금 더 진짜 같은 이미지들이 나오고 있기는 하지만, 생각보다는 성능이 썩 좋지 않네요.

 

 

다음으로는 복원 성능을 보겠습니다.

 

 

 

완전 초창기라서 사실상 이미지를 제대로 복원하지 못하고 있음을 확인할 수 있습니다.

 

 

 

 

 

100 에폭 동안 학습하고 난 결과 입니다. 9가 3처럼 나오는 등 살짝 문제가 있기는 하지만, 그래도 훨씬 더 복원 성능이 좋아졌습니다.

 

 

 

다음으로는, latent dimension을 15로 했을 때의 결과를 보여드리겠습니다.

 

 

 

이전보다 Generator 그래프와 Reconstruction 그래프는 훨씬 깔끔해진 것을 확인할 수 있었습니다.

 

 

반면에, Discriminator의 그래프가 영 심상치 않네요.

 

 

다음으로는, Test도 보겠습니다.

 

 

 

역시나 학습 초기라 멀쩡하지 못한 이미지가 나오고 있습니다.

 

 

 

뭔가 글씨의 모습이 썩 좋지 못하게 나왔습니다. 오히려 잠재 공간이 2차원일 때 보다 더욱 안 좋아진 것 같습니다.

 

 

다음으로는 복원 성능도 보겠습니다.

 

 

 

 

latent 차원이 15차원일 때, 복원 성능은 엄청나게 좋아진 것을 확인할 수 있습니다.

 

Decoder 성능이 매우 안 좋게 나왔음에도 15차원의 결과를 여기에 담게 된 이유가 바로 복원 성능 때문인데요.

 

latent dimension이 2일 때는 100 epoch 정도 돌면 대략 reconstruction error가 110 ~ 120 정도가 나옵니다.

 

하지만 latent dimension이 15일 때는 100 epoch정도 돌면 대략 reconstruction error가 65 ~ 70 정도가 나옵니다.

 

이를 통해 latent dimension이 증가할 수록 reconstruction error가 좋아질 수 있다는 사실을 확인할 수 있었습니다.

 

다만, Decoder의 성능이 안 좋아지는 문제가 있어서 약간 아쉬움이 남습니다.

 

 

 

마지막으로, latent vector의 값을 (-10, -10)부터 (10, 10)까지 균등하게 이동시키면서 복원했을 때 숫자가 어떻게 변하는지를 나타내는 그림을 보여드리고 마무리 지으려고 합니다.

 

 

 

해당 그림을 그리는 코드는, 제 Github에 올라가 있으니 확인해보시면 되겠습니다.

 

(모델과는 크게 관련이 없어 따로 해당 포스팅에서는 다루지 않습니다.)

 

 

 

개인적으로는 굉장히 관심이 있었던 모델임에도 불구하고, 생각보다 논문에 나온 것 처럼 깔끔한 성능을 내기가 너무 어려웠다는 점이 아쉬웠습니다.

 

 

모델의 구조를 이해하거나 이런 부분이 어려운건 아니였지만, 막상 구현했을 때 논문에 나온 성능이 나와야 의미가 있는 것이겠죠.

 

 

생성되는 것을 봐서는 모델 구조를 잘못 짰다거나 하진 않은 것 같은데, 쉽지 않네요 ㅠㅠ

 

 

추후에 이 문제를 해결할 수 있는 방법을 알게 된다면 해결해보도록 하겠습니다.

 

 

해당 포스팅에 사용된 코드는 다음 Github 주소에 올라가 있습니다.

 

github.com/PeterKim1/paper_code_review

 

 

 

 

 

 

오늘은 Autoencoder의 구조와 GAN framework를 결합해 탄생한 AAE에 대해서 알아보도록 하겠습니다.

 

 

paper : arxiv.org/abs/1511.05644

 

Adversarial Autoencoders

In this paper, we propose the "adversarial autoencoder" (AAE), which is a probabilistic autoencoder that uses the recently proposed generative adversarial networks (GAN) to perform variational inference by matching the aggregated posterior of the hidden co

arxiv.org

 

 

Abstract

 

 

이번 논문에서는 autoencoder의 hidden code vector의 aggregated posterior를 임의의 prior distribution과 매칭 하여 variational inference를 수행하기 위해 최근에 제안된 generative adversarial networks를 사용하는 확률적 autoencoder인 "adversarial autoencoder" (AAE)을 제안한다.

 

Aggregated posterior를 prior에 매칭시키는 것은 prior space의 특정 부분에서 생성하는 것이 의미 있는 샘플을 가져옴을 보장한다.

 

그 결과로, adversarial autoencoder의 decoder는 도입된 prior를 data distribution으로 mapping 하는 deep generative model을 학습한다.

 

우리는 semi-supervised classification, disentangling style and content of images, unsupervised clustering, dimensionality reduction and data visualization과 같은 응용 분야에서 사용될 수 있음을 보인다.

 

MNIST와 Street View House Numbers, Toronto Face dataset에서 실험을 수행하였으며, adversarial autoencoders가 generative modeling과 semi-supervised classification task에서 경쟁력 있는 결과를 나타냄을 보였다.

 

 

1. Introduction

 

 

Audio나 image, 혹은 video와 같은 풍부한 분포를 포착하기 위해 scalable generative model을 만드는 것은 machine learning의 중요한 도전 중 하나이다.

 

최근까지, Restricted Boltzmann Machines (RBM), Deep Belief Networks (DBNs), 그리고 Deep Boltzmann Machines (DBMs)와 같은 deep generative models들은 주로 MCMC 기반의 알고리즘에 의해서 학습되어 왔다.

 

이러한 접근법에서 MCMC 방법은 학습이 진행될수록 더욱 애매해지는 log-likelihood의 gradient를 계산한다.

 

이는 Markov Chains에서 나온 샘플들이 modes 사이에서 충분히 빠르게 혼합될 수 없기 때문이다.

 

최근에, direct back-propagation을 통해서 학습되고 MCMC 학습에서 마주하게 되는 어려움들을 회피할 수 있는 generative model이 개발되어져 왔다.

 

예를 들어, variational autoencoder (VAE) 혹은 importance weighted autoencoders는 잠재 변수에 대한 posterior distribution을 예측하는 recognition network를 사용하였고, generative adversarial networks (GAN)는 back-propagation을 통해서 네트워크의 output distribution을 직접적으로 형성하기 위해 adversarial training procedure를 사용했고 generative moment matching networks (GMMN)은 데이터 분포를 학습하기 위해 moment matching cost function을 사용하였다.

 

본 논문에서는 autoencoder를 generative model로 전환할 수 있는 adversarial autoencoder (AAE)라고 불리는 일반적인 접근 방식을 제안한다.

 

우리 모델에서, autoencoder는 전통적인 reconstruction error criterion와 autoencoder의 latent representation의 aggregated posterior distribution을 임의의 prior distribution으로 매칭 하는 adversarial training criterion의 dual objectives를 가지고 학습된다.

 

우리는 이 training criterion이 VAE 학습과 강한 연관이 있음을 보였다.

 

학습의 결과로 encoder는 data distribution을 prior distribution으로 변환하도록 학습하며 decoder는 imposed prior를 data distribution으로 mapping하는 deep generative model을 학습한다.

 

(이번 논문에서 가장 핵심되는 내용들이라 밑줄과 볼드체로 표시하였습니다. 해당 내용을 숙지하시고 앞으로 논문 내용을 보시면 좋을 것 같습니다.)

 

Figure 1: adversarial autoencoder의 아키텍처. 위의 행은 이미지 latent code $z$로부터 이미지 $x$를 복원하는 일반적인 autoencoder이다. 아래 행은 한 샘플이 autoencoder의 hidden code로부터 나온 것인지, 혹은 유저에 의해서 정해진 sampled distribution으로부터 나온 것인지를 예측하도록 학습된 두 번째 네트워크를 나타낸다.

 

 

1.1 Generative Adversarial Networks

 

 

Generative Adversarial Networks (GAN) framework는 generative model $G$와 discriminative model $D$의 두 신경망 사이의 min-max adversarial game을 만든다.

 

The discriminator model $D(x)$는 data space에 있는 point $x$가 우리의 generative model로부터 나온 샘플(negative samples)이라기보다는 우리가 모델링하려고 시도하고 있는 data distribution으로부터 나온 샘플(positive samples) 일 확률을 계산하는 신경망이다. 

 

동시에, generator는 prior $p(z)$로부터 나온 샘플 $z$를 data space로 mapping하는 함수 $G(z)$를 사용한다.

 

$G(z)$는 discriminator가 샘플들이 data distribution에서 생성되었다고 믿도록 최대한 속게끔 학습된다.

 

Generator는 $D(x)$의 $x$에 대한 gradient를 활용하여 학습하게 되며, 이를 사용해 generator의 parameter를 수정한다.

 

이 게임의 해결책은 다음과 같이 표현될 수 있다.

 

 

Generator $G$와 discriminator $D$는 두 단계에서 교대로 적용되는 SGD를 사용하여 확인할 수 있다.

 

(a) discriminator는 generator에 의해서 생성된 fake samples로부터 true samples를 구별하도록 학습한다.

 

(b) 생성된 샘플을 가지고 discriminator를 속이기 위해서 generator를 학습한다.

 

(GAN과 관련해서는 cumulu-s.tistory.com/22 에서 이미 다뤘기 때문에, 혹시 GAN에 대한 background 지식이 없으신 분들은 해당 포스트를 참고하셔서 GAN에 대한 내용을 확인하시면 되겠습니다.)

 

 

 

2. Adversarial Autoencoders

 

 

$x$를 input이라 하고 $z$를 deep encoder와 decoder를 가진 autoencoder의 latent code vector (hidden units)이라고 하자.

 

$p(z)$를 codes에 대해서 우리가 도입하길 원하는 prior distribution이라 하고, $q(z|x)$는 encoding distribution, $p(x|z)$는 decoding distribution이라 하자.

 

또한, $p_d(x)$는 data distribution이라 하고 $p(x)$는 model distribution이라 하자.

 

Autoencoder의 encoding function $q(z|x)$는 autoencoder의 hidden code vector에 대해서 aggregated posterior distribution $q(z)$를 다음과 같이 정의한다.

 

 

Adversarial autoencoder는 aggregated posterior $q(z)$를 임의의 prior $p(z)$에 매칭 시킴으로써 regularized 되는 autoencoder이다.

 

그러기 위해서, adversarial network는 Figure 1에서 나타난 것처럼 autoencoder의 hiddne code vector의 위쪽에 부착된다.

 

$q(z)$가 $p(z)$에 매칭되도록 안내하는 것은 adversarial network이다.

 

그동안에, autoencoder는 reconstruction error를 최소화하도록 시도한다.

 

또한, Adversarial network의 generator는 autoencoder의 encoder $q(z|x)$이다.

 

Encoder는 aggregated posterior distribution이 discriminative adversarial network가 hidden code $q(z)$이 true prior distribution $p(z)$로부터 왔다고 생각하도록 속일 수 있다는 것을 보장한다.

 

Adversarial network와 autoencoder 둘 다 reconstruction phase와 regularization phase라는 두 단계에 걸쳐 SGD를 활용해 공동으로 학습되며, mini-batch로 수행된다.

 

Reconstruction phase에서, autoencoder는 encoder와 decoder를 input의 reconsturction error를 최소화하도록 업데이트한다.

 

Regularization phase에서, adversarial network는 첫 번째로 discriminative network를 prior를 사용해서 생성된 true sample을 autoencoder에 의해서 계산된 hidden code로부터 생성된 샘플과 구별하도록 학습한다.

 

그러고 나서 autoencoder의 encoder이기도 한 generator가 discriminative network를 속이도록 업데이트한다.

 

한 번 학습 절차가 마무리되면, autoencoder의 decoder는 imposed prior $p(z)$를 data distribution으로 mapping 하는 generative model을 정의할 수 있다.

 

Adversarial autoencoder의 encoder $q(z|x)$에 대한 여러 가지 가능한 선택이 존재한다.

 

(1) Deterministic: 이 경우 우리는 $q(z|x)$를 $x$의 deterministic function이라고 가정한다. 이 경우에, encoder는 standard autoencoder의 encoder와 유사하고, $q(z)$에서 확률성의 유일한 원천은 data distribution $p_d(x)$이다.

 

(2) Gaussian posterior: 이 경우 우리는 $q(z|x)$를 Gaussian distribution이라고 가정하며, 이 분포의 평균과 분산은 encoder network에 의해서 예측된다: $z_i \sim N(\mu_i(x), \sigma_i(x))$.

 

이 경우에, $q(z)$에서의 확률성은 encoder의 output에서의 데이터 분포와 Gaussian distribution의 무작위성 모두로부터 나온다. 

 

우리는 encoder network를 통한 back-propagation을 위해 VAE의 re-parametrization trick을 사용할 수 있다.

 

(3) Universal approximator posterior: Adversarial autoencoder는 $q(z|x)$를 posterior의 universal approximator로 학습하는 데 사용될 수 있다.

 

Adversarial autoencoder의 encoder network를 input $x$와 고정된 분포(예를 들어, Gaussian)를 가지는 random noise $\eta$를 입력으로 받는 함수 $f(x, \eta)$라고 가정하자.

 

우리는 $\eta$의 다른 샘플에 대해서 $f(x, \eta)$를 평가함으로써 임의의 posterior distribution $q(z|x)$에서 샘플링할 수 있다.

 

다르게 말해서, 우리는 $q(z|x, \eta) = \delta(z - f(x,\eta))$로 가정할 수 있고 posterior $q(z|x)$와 aggregated posterior $q(z)$는 다음과 같이 정의된다.

 

 

이 경우에, $q(z)$에서의 확률성은 encoder의 input에서 데이터 분포와 random noise $\eta$ 모두에게서 나오며, posterior $q(z|x)$는 더 이상 Gaussian으로 제약되지 않고 encoder는 input $x$가 주어졌을 때 임의의 posterior distribution을 학습할 수 있다.

 

Aggregated posterior $q(z)$로부터 샘플링을 하는 효율적인 방법이 있기 때문에, adversarial training procedure는 encoder network $f(x, \eta)$를 통해서 direct back-propagation을 통해 $q(z)$를 $p(z)$에 매칭 할 수 있다.

 

 

다른 종류의 $q(z|x)$를 선택하는 것은 다른 training dynamics를 가지는 다른 종류의 모델을 야기할 것이다.

 

예를 들어, $q(z|x)$의 deterministic case에서, network는 오직 데이터 분포의 확률성을 이용하는 것을 통해 $q(z)$를 $p(z)$로 매칭해야 한다.

 

하지만 데이터의 empirical distribution이 training set에 의해서 고정되고 mapping이 deterministic 하기 때문에, 이는 매우 smooth하지 않은 $q(z)$를 만들게 될 것이다.

 

그러나, Guassian이나 universal approximator case에서 network는 $q(z)$를 smoothing out 함으로써 adversarial regularization stage에서 도움이 될 수 있는 확률성의 추가적인 원천에 접근할 수 있다.

 

그럼에도 불구하고, 광범위한 hyper-parameter search 후에, 우리는 $q(z|x)$의 각 유형에 대한 유사한 test-likelihood를 얻었다.

 

따라서 논문의 나머지에서 우리는 $q(z|x)$의 deterministic version에 대한 결과만 보고한다.

 

 

2.1 Relationship to Variational Autoencoders

 

 

우리의 연구는 spirit(정신?)에서 variational autoencoder와 유사하다.

 

하지만 VAE는 autoencoder의 hidden code vector에 prior distribution을 도입하기 위해 KL divergence penalty를 사용하였으나, 우리는 hidden code vector의 aggregated posterior를 prior distribution과 일치시킴으로써 adversarial training procedure를 사용한다.

 

VAE는 다음의 $x$의 negative log-likelihood에 대한 upper-bound를 최소화하였다.

 

 

Aggregated posterior $q(z)$는 Equation 1에 정의되었으며, $q(z|x)$를 Gaussian 분포라고 가정하고 $p(z)$를 임의의 분포라고 가정한다.

 

Variational bound는 3개의 term을 포함한다. 

 

첫 번째 term은 autoencoder의 reconstruction term으로 볼 수 있으며, 두 번째와 세 번째는 regularization term으로 볼 수 있다.

 

Regularization term이 없다면, 모델은 단순히 input을 복원하는 standard autoencoder이다.

 

하지만, regularization term의 존재로, VAE는 $p(z)$와 호환이 되는 latent representation을 학습한다.

 

Cost function의 두 번째 term은 posterior distribution의 큰 variance를 유도하지만, 세 번째 term은 prior $p(z)$와 aggregated posterior $q(z)$사이의 cross-entropy를 최소화한다.

 

Equation (2)에서 KL divergence나 cross-entropy term은 $q(z)$가 $p(z)$의 mode를 선택하도록 유도한다.

 

Adversarial autoencoder에서, 두 번째 2 개의 term을 $q(z)$가 $p(z)$의 전체 분포에 일치하도록 유도하는 adversarial training procedure로 대체한다.

 

Figure 2: MNIST에서 adversarial autoencoder와 variational autoencoder의 비교. Adversarial autoencoder에 대해서 hold-out image(Test set을 의미한다고 보시면 됩니다.) 들의 hidden code $z$를 (a) 2-D Gaussian에 fitting 시켰을 때와 (b) 2-D Gaussian의 10개의 mixture에 fitting 시켰을 때의 결과이다. 각 색깔은 관련된 label을 나타낸다. Variational autoencoder에도 동일하게 (c) 2-D Gaussian과 (d) 10개의 2-D Gaussian의 혼합에 fitting 시킨 결과이다. (e) 2-D Gaussian adversarial autoencoder에서 각 hidden code dimension $z$를 따라서 Gaussian 백분위수를 균일하게 샘플링해 만들어진 이미지이다.

 

이번 section에서, code distribution에 대해 지정된 prior distribution $p(z)$를 도입하는 adversarial autoencoder의 능력을 VAE와 비교한다. 

 

Figure 2a는 hidden code $z$에 구형의 2-D Gaussian prior distribution이 부과되는 MNIST 숫자 데이터에 훈련된 adversarial autoencoder에서 비롯되는 test data의 coding space $z$를 보여준다.

 

Figure 2a에 나타난 학습된 manifold는 sharp transition을 드러내고 있으며, 이는 coding space가 채워져 있고 구멍이 없음을 나타낸다. 

 

실제로, coding space에서의 sharp transition은 $z$내에서 interpolate 해서 만들어진 이미지들이 data manifold (Figure 2e)에 놓인다는 것을 나타낸다.

 

대조적으로, Figure 2c는 adversarial autoencoder 실험에서 사용된 것과 동일한 architecture를 가지는 VAE의 coding space를 보여준다.

 

이 경우에 VAE가 대략 2-D Gaussian distribution의 모습과 일치함을 볼 수 있다.

 

하지만, coding space의 여러 local 지역에 mapping 된 데이터 포인트가 없는 것은 VAE가 adversarial autoencoder와 같이 data manifold를 포착하지 못함을 나타낸다.

 

Figure 2b와 2d는 도입된 분포가 2-D Gaussian의 10개 mixture일 때 adversarial autoencoder와 VAE의 code space를 보여준다.

 

Adversarial autoencoder는 성공적으로 aggregated posterior를 prior distribution에 일치시켰다. (Figure 2b)

 

대조적으로, VAE는 10개의 Gaussian mixture와 체계적인 차이를 보여주고 있으며, 이는 위에서 설명한 것과 같이 VAE가 distribution의 mode를 매칭 시키는데 집중하기 때문인 것을 나타낸다.

 

VAE와 adversarial autoencoder 사이의 중요한 차이점은, VAE에서는 Monte-Carlo sampling에 의해서 KL Divergence를 통해 back-propagate 하기 위해 prior distribution의 정확한 함수 형태를 알고 있어야 한다.

 

하지만, AAE에서는 $q(z)$를 $p(z)$와 일치하도록 유도하기 위해서 prior distribution으로부터 샘플링하는 것이 가능하기만 하면 된다.

 

Section 2.3에서, adversarial autoencoder가 distribution의 정확한 함수 형태를 모르더라도 Swiss roll 분포와 같은 복잡한 분포를 도입할 수 있음을 보인다.

 

 

2.2 Relationship to GANs and GMMNs

 

이 부분은 생략합니다. 

 

 

 

2.3 Incorporating label information in the Adversarial Regularization

 

 

데이터가 라벨링이 되어 있는 경우에, hidden code의 분포를 더 잘 만들어 내기 위해 adversarial training stage에서 label information을 포함시킬 수 있다.

 

이번 section에서, autoencoder의 latent representation을 더욱 강하게 regularize 하기 위해 부분적인 혹은 완전한 label information을 어떻게 활용할 수 있는지를 설명한다.

 

이 아키텍처를 설명하기 위해서, adversarial autoencoder를 2-D Gaussian의 10개 mixture에 fitting 시킨 Figure 2b로 돌아간다.

 

이제 우리는 Gaussian distribution의 mixture의 각 mode가 MNIST의 label을 나타내도록 강제하는 것을 목표로 한다.

 

 

Figure 3는 이러한 semi-supervised 접근법을 위한 학습 절차를 나타낸다.

 

우리는 distribution의 mode와 label을 연관시키기 위해서 discriminative network의 input에 one-hot vector를 추가한다.

 

One-hot vector는 class label이 주어졌을 때 이에 대응되는 discriminative network의 decision boundary를 선택하는 switch로 작용한다.

 

이 one-hot vector는 unlabeled examples에 대해서 extra class를 가진다.

 

예를 들어, 2-D Gaussian의 10개 mixture를 도입하는 경우(Figure 2b and 4a)에 one-hot vector는 11개의 클래스를 포함한다.

 

첫 번째 10개의 class 각각은 대응되는 각각의 mixture component에 대한 decision boundary를 선택한다.

 

One-hot vector에 있는 여분의 class는 unlabeled training point에 대응된다.

 

Unlabeled point가 모델에 제시되었을 때, extra class는 켜지고, Gaussian distribution의 전체 mixture를 위한 decision boundary를 선택한다.

 

Adversarial training의 positive phase 동안에, one-hot vector를 통해 discriminator에 positive sample이 뽑힌 mixture component의 label을 제공한다.

 

Unlabeled examples를 위해 제공되는 positive samples는 특정 class가 아닌 Gaussian의 전체 mixture에서 나온다.

 

Negative phase 동안에, training point image의 label을 one-hot vector를 통해서 discriminator에 제공한다.

 

Figure 4: hidden code를 더 잘 규제하기 위해 label information을 활용한 경우. Top Row: coding space가 10개의 2-D Gaussian mixture와 일치하기 위해서 학습된 경우: (a) hold-out image의 coding space z (b) 첫 번째 3 mixture component의 manifold: 각 패널은 대응되는 mixture component의 축을 따라 Gaussian percentile을 균등하게 샘플링했을 때 생성되는 이미지들을 포함한다. Bottom Row: 동일하지만 swiss roll distribution일 때. Label은 숫자 순서대로 mapping 됨. (즉, swiss roll의 첫 번째 10%는 숫자 0에 대응되며, 나머지는 동일) (c) hold-out image의 coding space z (d) main swiss roll axis를 따라 걸으면서 생성된 샘플들

 

Figure 4a는 1만 개의 labeled MNIST와 4만 개의 unlabeled MNIST 예제에 대해서 훈련된 10개의 2-D Gaussian의 혼합을 prior로 훈련된 adversarial autoencoder의 latent representation을 나타낸다.

 

이 경우에, prior의 $i$번째 mixture components는 semi-supervised 방식으로 $i$번째 class에 부여된다.

 

Style representation은 각 mixture component 내에서는 일관적으로 표현되며, 이것은 class와 독립이다.

 

예를 들어, Figure 4b의 모든 패널의 왼쪽 상단 영역은 곧게 쓰인 style에 대응되고, 오른쪽 하단 영역은 기울어진 스타일에 대응된다.

 

이 방법은 MNIST data를 "swiss roll" (평균이 swiss roll 축의 길이를 따라서 균등하게 분포되는 조건부 Gaussian distribution)에 mapping 하는 것을 통해서 검증되는 것처럼 parametric form이 없는 임의의 분포에도 확장될 수 있다.

 

Figure 4c는 coding space z를 묘사하고 있으며, Figure 4d는 latent space에서 swiss roll axis를 따라서 걸음으로써 생성되는 이미지들을 강조한다.

 

 

 

3. Likelihood Analysis of Adversarial Autoencoders

 

해당 논문에서 사용하고 있는 metric이 GAN paper에서 사용된 metric과 유사한데, 요즘은 잘 사용하지 않는 것 같아서 해당 부분도 제외합니다.

 

 

4. Supervised Adversarial Autoencoders

 

 

semi-supervised learning은 machine learning에서 오랫동안 지속되어 온 개념적인 문제이다.

 

최근에, 생성 모델들은 원칙적인 방식으로 class label information을 많은 다른 잠재적인 variation의 요소로부터 분리할 수 있기 때문에 semi-supervised learning에 대한 가장 인기 있는 접근법 중 하나가 되었다.

 

 

이번 section에서는, 먼저 fully supervised scenarios에 집중하고, 이미지 style information으로부터 class label information을 분리할 수 있는 adversarial autoencoder의 구조에 대해서 논의해본다.

 

그러고 나서 이 구조를 Section 5에서의 semi-supervised setting으로 확장한다.

 

Label information을 포함시키기 위해서, 우리는 decoder에 label의 one-hot vector encoding을 제공하기 위해 Figure 1의 네트워크 아키텍처를 Figure 6의 형태로 변경한다.

 

Decoder는 label을 확인하는 one-hot vector와 이미지를 reconstruct 하는 hidden code z를 모두 활용할 수 있다.

 

이 아키텍처는 hidden code z에서 label과 독립적인 모든 정보를 네트워크가 유지하도록 강제한다.

 

Figure 7a는 hidden code가 15-D Gaussian이도록 설정된 네트워크를 MNIST 숫자에 학습되었을 때의 결과를 보여준다. 

 

Figure 7a의 각 행은 hidden code $z$가 특정한 값으로 고정되지만 레이블이 변하면서 만들어진 복원된 이미지를 나타낸다.

 

주어진 행에 대해서 복원된 이미지의 style은 일정하다.

 

Figure 7b는 같은 실험을 Street View House Numbers dataset에 적용한 결과를 보여준다. SVHN style manifold를 보여주는 비디오는 다음 주소에서 볼 수 있다. (주소가 있긴 했는데, 눌러보니 안 되네요. 아마 링크가 변한 것 같아요.)

 

 

이번 실험에서, one-hot vector는 이미지에서 central digit과 연관된 라벨을 나타낸다.

 

각 row에서 style information은 가장 왼쪽과 가장 오른쪽 숫자의 라벨과 관련된 정보를 포함하게 되는데, 이는 맨 왼쪽과 맨 오른쪽 숫자는 one-hot encoding으로 label information이 제공되지 않기 때문이다.

 

 

5. Semi-supervised Adversarial Autoencoders

 

 

Section 4를 기반으로 해서, labeled data만을 사용해서 얻을 수 있는 분류 성능을 unlabeled data의 generative description을 활용하여 향상하는 semi-supervised learning을 위한 모델을 개발하기 위해 adversarial autoencoder를 사용한다.

 

구체적으로 말하자면, 데이터가 Categorical distribution에서 만들어진 latent class variable $y$와 Gaussian distribution에서 만들어진 연속형 잠재 변수 $z$에 의해서 생성되었다고 가정한다.

 

 

우리는 Figure 6의 네트워크 구조를 바꿔서 AAE의 inference network가 encoder $q(z, y|x)$를 사용하여 discrete class variable $y$와 연속형 잠재 변수 $z$를 예측하도록 만든다. (Figure 8 참조)

 

Decoder는 one-hot vector로 되어 있는 class label과 연속형 hidden code $z$를 활용하여 이미지를 복원한다.

 

여기에는 autoencoder의 hidden representation을 규제하기 위한 두 개의 별도의 adversarial network가 존재한다.

 

첫 번째 adversarial network는 Categorical distribution을 label representation으로 강제한다.

 

이 adversarial network는 latent class variable $y$가 어떠한 style information도 가지지 않도록 보장하며, $y$의 aggregated posterior distribution이 Categorical distribution과 매칭 된다는 것을 보장한다.

 

두 번째 adversarial network는 Gaussian distribution을 style representation으로 강제하며 이는 latent variable $z$가 연속형 Gaussian variable임을 보장한다.

 

 

Adversarial network 양쪽 모두와 autoencoder는 SGD를 이용해 reconstruction phase, regularization phase, and semi-supervised classification phase로 이루어진 3 phase 동안 공동으로 학습된다.

 

1) Reconstruction phase에서, autoencoder는 encoder $q(z, y|x)$와 decoder를 unlabeled mini-batch에서 input의 reconstruction error를 최소화하도록 업데이트한다.

 

2) Regularization phase에서, 각 adversarial network는 첫 번째로 각자의 discriminative network가 실제 샘플(Categorical and Gaussian prior를 사용해서 만들어진)을 생성된 샘플(autoencoder에 의해서 계산된 hidden codes)로부터 구별하도록 업데이트한다.

 

Adversarial networks는 그다음으로 그들의 discriminative networks를 혼란스럽게 만들도록 generator를 업데이트한다.

 

3) Semi-supervised classification phase에서, autoencoder는 $q(y|x)$가 labeled mini-batch에서 cross-entropy cost를 최소화하도록 학습된다.

 

 

MNIST와 SVHN에 대한 semi-supervised classification 실험의 결과는 Table 2에서 확인할 수 있다.

 

100개와 1000개의 label을 가지는 MNIST dataset에 대해서, AAE의 성능은 VAE에 비해서 상당히 좋았으며, VAT와 CatGAN과 비슷하였고, 하지만 Ladder networks와 ADGM가 더 좋은 성능을 냈다.

 

우리는 또한 supervised AAE를 모든 이용 가능한 label에 학습시켰으며 error rate 0.85%를 얻었다.

 

이와 비교해서, 같은 구조를 가지고 있는 dropout supervised neural network는 전체 MNIST dataset에 대해서 1.25%의 error rate를 나타냈으며, 이는 adversarial training의 regularization effect를 강조한다.

 

1000개의 label을 가지는 SVHN dataset에 대해서는, AAE는 ADGM에 의해 나타난 SOTA classification performance와 거의 일치했다.

 

또한 모든 AAE model은 end-to-end로 학습되었다는 것을 언급할 가치가 있으며, 반면에 semi-supervised VAE model은 한 번에 한 layer씩 학습되어야 한다.

 

 

6. Unsupervised Clustering with Adversarial Autoencoders

 

 

이전 section에서는, 제한된 label information을 가지고 adversarial autoencoder가 강력한 semi-supervised representations을 학습할 수 있음을 보였다.

 

하지만, 어떠한 supervision 없이 unlabeled data으로부터 "강력한" representation을 학습할 수 있는지 없는지에 대한 질문은 아직도 답변되지 않은 채로 남아있다.

 

이번 section에서는, adversarial autoencoder가 순수하게 unsupervised fashion에서 연속적인 latent style variable로부터 discrete class variable을 구분할 수 있는지를 보인다.

 

우리가 사용한 아키텍처는 Figure 8와 유사하지만, 차이가 있다면 semi-supervised classification stage를 제거했다는 점이다.

 

따라서, 더 이상 이 모델을 labeled mini-batch에 학습시키지 않아도 된다.

 

또 다른 차이점은 inference network $q(y|x)$가 데이터가 모이기를 바라는 범주의 수를 차원으로 갖는 one-hot vector를 예측한다는 점이다.

 

 

 

Figure 9은 cluster의 수를 16으로 했을 때 MNIST에 학습된 AAE의 unsupervised clustering의 성능을 나타낸 것이다.

 

각 행은 하나의 cluster에 대응된다.

 

각 행의 첫 번째 이미지는 cluster head를 나타내며, 이는 style variable을 0으로 고정하고 label variable을 16 one-hot vector 중 한 개로 설정했을 때 만들어지는 숫자이다.

 

각 행에서 나머지 이미지들은 $q(y|x)$를 기반으로 대응되는 카테고리로 분류된 랜덤 테스트 이미지들이다.

 

 

우리는 AAE가 class label로 어떤 discrete style을 선택한다는 것을 볼 수 있다.

 

예를 들어서, 기울어진 숫자 1과 6 (cluster 16과 11)은 곧게 선 1과 6 (cluster 15와 10)과 별개의 군집에 놓여 있으며, 혹은 네트워크는 숫자 2를 이를 고리 모양으로 쓰였는지 아닌지에 따라 두 개의 군집(cluster 4, 6)으로 분리했다.

 

 

우리는 AAE의 unsupervised clustering 성능을 평가하기 위해 실험을 수행했으며, 다음과 같은 평가 protocol을 사용했다.

 

학습이 끝난 후에, 각 cluster $i$에 대해서, $q(y_i|x_n)$을 최대화하는 validation example $x_n$을 찾고, $x_n$의 label을 cluster $i$의 모든 포인트에 적용한다. 그러고 나서 각 cluster에 assign 된 class label을 기반으로 test error를 계산한다.

 

Table 3에서 보이는 것처럼, AAE는 16개, 30개의 전체 라벨을 가지는 경우 9.55%와 4.10%의 classification error rate를 나타냈다. 

 

cluster의 수가 증가할수록 classification rate가 증가함을 확인하였다.

 

 

7. Dimensionality Reduction with Adversarial Autoencoders

 

 

고차원 데이터의 시각화는 데이터 생성 과정에 대한 이해를 촉진시키고 데이터에 대한 유용한 정보를 추출하도록 해준다는 점에서 많은 applications에서 매우 중요한 문제이다.

 

가장 흔하게 사용되는 데이터 시각화 방법은 근처의 point가 유사한 object에 대응되도록 저차원의 embedding을 학습하는 것이다.

 

지난 수십 년간, t-SNE와 같은 non-parametric dimensionality reduction techniques들이 계속해서 제안되어 왔다.

 

이러한 방법들의 주요한 문제점은 새로운 데이터 포인트의 embedding을 찾는 데 사용될 수 있는 parametric encoder를 가지고 있지 않다는 점이다.

 

Parametric t-SNE와 같은 다른 방법들은 이 문제를 해결하기 위해 제안되었다.

 

 

Autoencoder는 그러한 embedding을 위해 요구되는 non-linear mapping을 제공하기 때문에 흥미로운 대안이 된다.

 

하지만, non-regularized autoencoder는 manifold를 많은 다른 domain으로 균열시킨다는 사실이 널리 알려져 있으며, 이는 유사한 이미지에 대해서 매우 다른 code를 갖도록 만든다.

 

 

이번 section에서, 우리는 dimensionality reduction과 data visualization 목적을 위한 adversarial autoencoder 아키텍처를 제시한다.

 

이러한 autoencoder에서, adversarial regularization이 유사한 이미지들의 hidden code를 서로 붙게끔 만든다는 것을 보여줄 것이며, 따라서 autoencoder에 의해서 학습된 embedding에서 전형적으로 마주하게 되는 manifold fracturing problem을 방지한다는 것을 보여줄 것이다.

 

 

우리가 $m$ class label을 가지는 데이터셋을 가지고 있고 데이터셋의 차원을 $n$으로 줄이려고 한다고 가정하자.

 

시각화를 목적으로 할 때는 $n$은 보통 2나 3이 된다. 

 

Figure 8의 아키텍처를 final representation을 $n$차원의 style representation과 cluster head의 $n$차원의 distributed representation을 추가하여서 얻게 되는 Figure 10 아키텍처로 변경한다.

 

Cluster head representation은 $m$차원의 one-hot class label vector를 $m \times n$ matrix $W_C$를 곱해서 얻게 되며, $W_C$의 행들은 SGD에 의해서 학습된 $m$ cluster head representation을 나타낸다.

 

우리는 모든 두 cluster head 간의 Euclidean distance에 처벌을 가하기 위해 추가적인 cost function을 도입한다.

 

구체적으로, 만약 Euclidean distance가 threshold $\eta$보다 크다면, cost function은 0이며, 만약 $\eta$보다 작다면, cost function은 선형적으로 distance에 처벌을 가한다.

 

 

Figure 11(a, b)는 $n =2$차원으로 MNIST dataset ($m= 10$)에 대해 1000개와 100개의 label을 가지고 semi-supervised dimensionality reduction을 한 결과를 나타낸다.

 

network가 digit cluster를 깔끔하게 분리한다는 것을 확인할 수 있으며 각각 semi-supervised classification error 4.20%와 6.08%를 달성하였다.

 

2D 제약 때문에 classification error는 고차원의 경우보다 좋지 못하다. 그리고 각 cluster의 style distribution은 Gaussian이 아니다.

 

Figure 11c는 $n=2$차원에서 cluster의 수를 $m=20$으로 뒀을 때 unsupervised dimensionality reduction의 결과를 보여준다.

 

네트워크가 digit cluster와 sub-custer의 오히려 더 깔끔한 분리를 달성할 수 있음을 볼 수 있다.

 

예를 들어서, 네트워크는 숫자가 곧게 서 있는지 혹은 기울어져 있는지에 따라서 녹색 cluster인 두 개의 별개의 cluster로 숫자 1을 배치했다.

 

네트워크는 또한 숫자 6을 검은색 cluster인 3개의 cluster로 숫자가 얼마나 기울어졌는지에 따라 다르게 배치했다. 

 

또한 네트워크는 숫자 2를 빨간 cluster인 2개의 별도의 cluster로 고리 형태로 쓰였는지 아닌지에 따라 배치했다.

 

 

Figure 10에 나타난 AAE 아키텍처는 또한 이미지를 더 높은 차원($n$ > 2)으로 embedding 할 때 사용될 수 있다.

 

예를 들어서, Figure 11d는 $n = 10$차원일 때 100개의 label을 가질 때의 semi-supervised dimensionality reduction의 결과를 보여준다.

 

이 경우에, 우리는 $W_C$ matrix를 $W_C = 10I$로 고정하였으며, 이에 따라 cluster head는 10차원 simplex의 모서리에 위치한다.

 

Style representation은 10D Gaussian distribution에서 표준편차 1을 가지고 학습되었으며, final representation을 만들기 위해 cluster head에 추가되었다.

 

한번 네트워크가 학습되면, 10차원의 학습된 representation을 시각화하기 위해서 cluster head가 2D circle에 균일하게 위치한 points로 mapping 되도록 10D representation을 2D space로 mapping 하는 linear transformation을 사용하였다.

 

우리는 이 figure로부터 고차원의 경우에, style representation이 실제로 Gaussian distribution을 학습한다는 사실을 검증할 수 있었다.

 

전체 100개의 label을 가지는 경우에, 이 모델은 3.90%의 classification error-rate를 나타냈으며, 이는 Figure 8에 나온 concatenated style and label representation을 가지는 AAE 아키텍처에 의해서 달성된 1.90% classification error-rate보다 더 안 좋은 결과이다.

 

 

 

8. Conclusion

 

 

본 논문에서는 확률론적 autoencoders의 이산형 및 연속형 잠재 변수에 대한 variational inference algorithm으로 GAN framework를 사용할 것을 제안하였다.

 

우리의 방법은 adversarial autoencoder (AAE)라고 불리며, 이는 MNIST와 TFD에서 경쟁력 있는 test likelihood를 성취한 generative autoencoder이다.

 

우리는 이 방법이 어떻게 semi-supervised scenarios로 확장될 수 있는지에 대해서 논의하였으며, MNIST와 SVHN dataset에서 경쟁력 있는 semi-supervised classification performance를 나타냄을 보였다.

 

마지막으로, 이미지의 스타일과 내용을 구분하는 것, 비지도 군집화, 차원 축소 그리고 데이터 시각화에서의 adversarial autoencoder의 활용을 설명했다.

 

 

 

여기까지 해서 AAE 논문의 내용을 마무리하였습니다.

 

우리가 일반적으로 생각하는 Basic AAE의 내용만 찾으신다면 챕터의 앞부분만 읽으시면 충분하지만, 논문에서는 AAE를 활용할 수 있는 다양한 방법들을 제시하고 있어서 모든 내용을 다 다루는 것이 좋겠다고 판단, 모든 내용을 담았습니다.

 

이렇게 논문에서는 많은 활용 방법들을 제시하였는데, 논문의 공식 코드가 없다 보니 Github에 공개된 대부분의 코드들은 Basic AAE 정도만 다루고 있다는 점에서 아쉬움이 남습니다.

 

다음 글에서는 Basic AAE의 코드를 직접 작성해보면서 실험을 진행해보겠습니다.

 

 

 

 

해당 논문의 paper review : cumulu-s.tistory.com/24

 

2. Auto-Encoding Variational Bayes (VAE) - paper review

두 번째로 다뤄볼 논문은 VAE라는 이름으로 잘 알려진 Auto-Encoding Variational Bayes라는 논문입니다. 너무 유명한 논문이라 다양한 자료들이 많이 있지만, 가급적이면 다른 분들이 가공해서 만든 자료

cumulu-s.tistory.com

 

이번 글에서는 VAE를 실제로 구현한 코드와, 각 코드가 논문에서 어떤 것과 대응되는지를 자세히 알아보겠습니다.

 

 

paper review에서는 수많은 수식들이 나왔지만, 막상 구현에서는 그렇게까지 복잡하지 않습니다.

 

 

그럼 시작해보겠습니다.

 

import torch
import torchvision
import torchvision.transforms as transforms
import torch.nn as nn
import torch.optim as optim
from tqdm.auto import tqdm
from torch.nn import functional as F
import numpy as np
import matplotlib.pyplot as plt
from torch.utils.tensorboard import SummaryWriter
import datetime
import os

먼저, 필요한 패키지들을 불러옵니다.

 

이번에는 pytorch에서 지원하는 tensorboard라는 기능을 사용해서 loss function을 plotting 해보고, 생성되는 이미지들을 살펴보려고 합니다.

 

USE_CUDA = torch.cuda.is_available()
DEVICE = torch.device("cuda" if USE_CUDA else "cpu")
print("사용하는 Device : ", DEVICE)

current_time = datetime.datetime.now() + datetime.timedelta(hours= 9)
current_time = current_time.strftime('%Y-%m-%d-%H:%M')

saved_loc = os.path.join('/content/drive/MyDrive/VAE_Result', current_time)
os.mkdir(saved_loc)

print("저장 위치: ", saved_loc)

writer = SummaryWriter(saved_loc)
EPOCHS = 50
BATCH_SIZE = 200

저번 GAN 코드에서와 달리, 저장 위치를 지정해주는 코드를 추가했습니다.

 

tensorboard를 사용하면, 코드가 돌아가면서 loss나 이미지가 찍히는데 이를 돌릴때마다 결과를 나눠서 가지고 있어야 하기 때문에 폴더를 별도로 만드는 방법을 사용했습니다.

 

datetime.datetime.now()를 치면 현재 시간이 나오는데, Google Colab의 경우는 한국 시간보다 9시간 느리기 때문에 datetime.timedelta(hours = 9)를 통해서 9시간을 더해 실제 한국 시간과 시차를 맞춰줍니다.

 

그리고 .strftime을 사용하면 원하는 형태로 출력이 되도록 만들 수 있습니다.

 

/content/drive/MyDrive/VAE_Result <= 이거는 제가 사용하는 경로이므로, 원하시는 경로로 바꿔서 지정해주시면 됩니다.

 

os.mkdir는 원하는 경로에 폴더를 생성하는 코드입니다. 이렇게 해야 돌릴 때마다 폴더가 새로 만들어지고, 만들어진 폴더에 tensorboard를 만드는데 필요한 데이터들이 저장되게 됩니다.

 

writer = SummaryWriter 를 이용해서 tensorboard를 써주는 객체를 만들어줍니다.

 

# Transformer code
transformer = transforms.Compose([
            transforms.ToTensor()
])


# Loading trainset, testset and trainloader, testloader
trainset = torchvision.datasets.MNIST(root = '/content/drive/MyDrive/MNIST', train = True,
                                        download = True, transform = transformer)

trainloader = torch.utils.data.DataLoader(trainset, batch_size = BATCH_SIZE, shuffle = True, num_workers = 2)


testset = torchvision.datasets.MNIST(root = '/content/drive/MyDrive/MNIST', train = False,
                                        download = True, transform = transformer)

testloader = torch.utils.data.DataLoader(testset, batch_size = BATCH_SIZE, shuffle = True, num_workers = 2)

transformer에는 numpy array를 pytorch tensor로 만들어주는 역할을 하는 transforms.ToTensor()만 투입해줍니다.

 

 

# sample check
sample, label = next(iter(trainloader))

# show grid image
def imshow_grid(img):
    img = torchvision.utils.make_grid(img)
    print(type(img))
    print(img.shape)
    plt.imshow(img.permute(1, 2, 0))
    ax = plt.gca()
    ax.axes.xaxis.set_visible(False)
    ax.axes.yaxis.set_visible(False)
    plt.show()


imshow_grid(sample[0:8])

 

해당 코드는 샘플로 8개의 이미지만 grid 형식으로 만들어서 plotting 하는 코드입니다.

 

 

# VAE model
class VAE(nn.Module):
    def __init__(self, image_size, hidden_size_1, hidden_size_2, latent_size):
        super(VAE, self).__init__()

        self.fc1 = nn.Linear(image_size, hidden_size_1)
        self.fc2 = nn.Linear(hidden_size_1, hidden_size_2)
        self.fc31 = nn.Linear(hidden_size_2, latent_size)
        self.fc32 = nn.Linear(hidden_size_2, latent_size)

        self.fc4 = nn.Linear(latent_size, hidden_size_2)
        self.fc5 = nn.Linear(hidden_size_2, hidden_size_1)
        self.fc6 = nn.Linear(hidden_size_1, image_size)

    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        h2 = F.relu(self.fc2(h1))
        return self.fc31(h2), self.fc32(h2)

    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mu + std * eps

    def decode(self, z):
        h3 = F.relu(self.fc4(z))
        h4 = F.relu(self.fc5(h3))
        return torch.sigmoid(self.fc6(h4))

    def forward(self, x):
        mu, logvar = self.encode(x.view(-1, 784))
        z = self.reparameterize(mu, logvar)
        return self.decode(z), mu, logvar

 

다음으로는, 가장 핵심이 되는 VAE model에 해당하는 class에 대해서 알아보겠습니다.

 

먼저 논문에서 $p_\phi(z|x)$인 Encoder(혹은 Recognition model)부터 보겠습니다.

 

Encoder는 이미지를 받아서, $\mu$와 $\sigma$를 출력해야 합니다.

 

따라서 이 작업이 self.fc1과 self.fc2, self.fc31 / self.fc32를 통해서 이루어집니다.

 

self.fc1는 이미지를 받아서 hidden space_1만큼으로 출력해내고, self.fc2는 hidden space_1만큼의 데이터를 받아서 hidden space_2만큼의 데이터를 뽑아냅니다. self.fc31와 self.fc32는 hidden space_2만큼의 데이터를 받아서 latent space 차원만큼의 $\mu$와 $\sigma$를 출력해냅니다.

 

이 작업은 encode라는 이름의 함수로 만들어 해당 작업이 이루어지게 코드가 짜져있습니다.

 

다음으로는, $\mu$와 $\sigma$가 주어졌을 때, latent variable $z$를 만들어야 합니다.

 

이 작업은 reparameterization이라는 이름으로 논문에서 소개되었고, 코드상에서는 reparameterize라는 함수로 구현되었습니다.

 

근데 잘 보면, 이 함수는 mu와 logvar를 받는다는 것을 확인할 수 있습니다.

 

갑자기 logvar는 무엇을 의미하는 것일까요?

 

이는 표준편차 값이 음수가 되지 않도록 만들기 위해서, encoder에서 나온 self.fc32의 결괏값을 $log\sigma^2$로 생각합니다. 

 

그래서 변수 이름이 logvar(log 분산)인 것이죠.

 

정리해보면, 이렇게 정리할 수 있습니다.

 

$\sigma = e^{log\sigma} = e^{2log\sigma/2} = e^{log\sigma^2/2} = e^{logvar/2}$가 됩니다.

 

이렇게 만들면, $\sigma$의 값이 $e^{logvar/2}$로 구현되기 때문에, 무조건 양수 값이 되게 됩니다. 

 

다시 reparameterize 함수로 돌아가면, 입력으로 받은 mu와 logvar를 가지고,

 

std는 torch.exp(0.5 * logvar)로 만들어주고, eps는 torch.randn_like(std)로 만들어줍니다.

 

torch.randn_like는 입력과 동일한 모양으로 평균이 0이고 분산이 1인 정규분포에서 숫자를 뽑아 tensor를 만들어줍니다.

 

이를 논문에서 나온 것처럼, mu + std * eps로 구현합니다.

 

이것의 결과를 z라는 이름으로 latent vector로 만들어주고, 이것을 decoding 한 결과와 mu, logvar를 출력으로 내보냅니다.

 

self.decode(z)를 해서 나오는 결과는, torch.sigmoid(self.fc6(h4))이므로 이미지의 사이즈와 동일한 차원을 가지면서 sigmoid를 통과해 0부터 1 사이의 값입니다. 

 

이는 우리가 input으로 투입시킨 이미지를 VAE를 통해서 복원한 이미지라고 볼 수 있습니다.

 

VAE_model = VAE(28*28, 512, 256, 2).to(DEVICE)
optimizer = optim.Adam(VAE_model.parameters(), lr = 1e-3)

다음은 VAE 모델을 VAE_model이라는 이름의 객체로 만들어주고, Adam optimizer를 만들어줍니다.

 

hidden space_1의 수는 512로 잡았고, hidden space_2의 수는 256, latent space의 차원은 2차원으로 지정하였습니다.

 

 

def loss_function(recon_x, x, mu, logvar):
    BCE = F.binary_cross_entropy(recon_x, x.view(-1, 784), reduction = 'sum')
    KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
    return BCE, KLD

다음 코드는 loss function을 계산하는 코드입니다.

 

먼저 논문에서 나온 loss 값(variational lower bound)을 살펴봅시다.

 

 

첫 번째 term은 KL-Divergence라는 얘기를 했었고, 두 번째 term은 reconstruction error입니다.

 

먼저, 논문의 Appendix B를 통해서 어떻게 이것이 도출되었는지 보겠습니다.

 

prior가 $p_\theta(z) = N(0, I)$를 만족시키고, posterior approximation이 $q_\phi(z|x^{(i)})$가 Gaussian이면 이렇게 풀 수 있다고 합니다.

 

맨 마지막을 보시면, - KL term을 한 결과가 바로 1/2로 시작하는 식임을 확인할 수 있습니다.

 

KL Divergence는 항상 양수이므로, - KL term은 항상 음수가 될 것입니다.

 

loss를 계산하고자 하는 것이므로, 실제 코드에서는 여기에 - 를 곱해주는 식으로 계산한 것으로 보입니다.

 

따라서 코드에서는 - 0.5 * torch.sum(1 + logvar - mu.pow(2) -logvar.exp())로 계산됩니다.

 

 

 

 

두 번째 reconstruction error항은 어떻게 구성되는지 Appendix C를 보면 알 수 있습니다.

 

우리 모델의 경우, decoder를 통해서 나오는 값이 sigmoid activation function을 통과해서 나오기 때문에 Bernoulli distribution을 따른다고 생각할 수 있습니다.

 

논문의 Appendix C에서는, $p_\theta(x|z)$가 multivariate Bernoulli 분포일 때, 다음과 같이 계산하라고 나와있습니다.

 

따라서, 이를 F.binary_cross_entropy()를 이용해서 계산하였습니다.

 

원래 코드에서는 BCE와 KLD를 더하도록 되어 있는데, 저는 BCE와 KLD의 학습 / 테스트 그래프를 그리기 위해서 두 값이 합쳐져서 나오는 게 아니라 별도로 output으로 나오도록 코드를 짰습니다.

 

 

def train(epoch, model, train_loader, optimizer):
    model.train()
    train_loss = 0
    for batch_idx, (data, _) in enumerate(train_loader):
        data = data.to(DEVICE)
        optimizer.zero_grad()

        recon_batch, mu, logvar = model(data)

        BCE, KLD = loss_function(recon_batch, data, mu, logvar)

        loss = BCE + KLD

        writer.add_scalar("Train/Reconstruction Error", BCE.item(), batch_idx + epoch * (len(train_loader.dataset)/BATCH_SIZE) )
        writer.add_scalar("Train/KL-Divergence", KLD.item(), batch_idx + epoch * (len(train_loader.dataset)/BATCH_SIZE) )
        writer.add_scalar("Train/Total Loss" , loss.item(), batch_idx + epoch * (len(train_loader.dataset)/BATCH_SIZE) )

        loss.backward()

        train_loss += loss.item()

        optimizer.step()

        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\t Loss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader),
                loss.item() / len(data)))
            
    print("======> Epoch: {} Average loss: {:.4f}".format(
        epoch, train_loss / len(train_loader.dataset)
    ))        

다음으로는 학습 코드입니다.

 

VAE에서는 label이 필요 없으므로, train_loader에서 나오는 label을 _로 표기해서 별도로 저장하지 않습니다.

 

data를 model에 넣으면, 아까 위에서 봤듯이 reconstruction 된 이미지와 mu, logvar가 나오게 됩니다.

 

그리고 이 값들을 이용해서 loss_function에 투입하여 loss 값을 계산합니다.

 

최종적인 loss 값은 BCE + KLD가 될 것이며, 이를 backpropagation 시켜줍니다.

 

중간에 writer.add_scalar라는 함수가 보이는데, 이는 tensorboard에 값을 저장하기 위해 추가된 코드입니다.

 

첫 번째인 "Train/Reconstruction Error"는 어떤 이름을 가지는 곳에 저장할 것인지를 정하는 것이고

 

두 번째인 BCE.item()은 tensorboard에 저장하려고 하는 값 그 자체를 나타냅니다.

 

그리고 세 번째 인자는 그래프를 그려줄 때 x축에 해당하는 값을 나타냅니다. 

 

batch_idx가 배치의 index이므로, 여기에 epoch이 지날 때마다 추가적으로 더 더해줘서

 

실제로 몇 번째의 batch인지를 x축의 값으로 넣도록 하였습니다.

 

MNIST의 경우, train data가 6만 장이므로, batch size = 200 기준으로는 1 epoch 당 300번이 그래프에 찍히게 됩니다.

 

해당 코드에서는 학습을 50 epochs 만큼 진행하므로, train 데이터에서는 x축의 값이 0부터 15000까지 찍힐 것입니다.

 

 

def test(epoch, model, test_loader):
    model.eval()
    test_loss = 0
    with torch.no_grad():
        for batch_idx, (data, _) in enumerate(test_loader):
            data = data.to(DEVICE)
            
            recon_batch, mu, logvar = model(data)
            BCE, KLD = loss_function(recon_batch, data, mu, logvar)

            loss = BCE + KLD

            writer.add_scalar("Test/Reconstruction Error", BCE.item(), batch_idx + epoch * (len(test_loader.dataset)/BATCH_SIZE) )
            writer.add_scalar("Test/KL-Divergence", KLD.item(), batch_idx + epoch * (len(test_loader.dataset)/BATCH_SIZE) )
            writer.add_scalar("Test/Total Loss" , loss.item(), batch_idx + epoch * (len(test_loader.dataset)/BATCH_SIZE) )
            test_loss += loss.item()

            if batch_idx == 0:
                n = min(data.size(0), 8)
                comparison = torch.cat([data[:n], recon_batch.view(BATCH_SIZE, 1, 28, 28)[:n]]) # (16, 1, 28, 28)
                grid = torchvision.utils.make_grid(comparison.cpu()) # (3, 62, 242)
                writer.add_image("Test image - Above: Real data, below: reconstruction data", grid, epoch)

다음으로는 test 코드입니다.

 

train과 다른 지점은 if batch_idx == 0:에 해당하는 부분일 것 같습니다.

 

torch.cat을 통해서 test_loader에서 나오는 데이터 8개와, 이를 VAE 모델을 통해서 뽑아낸 reconstruction 결과 8개를 합쳐줍니다. 이는 (16, 1, 28, 28)로 나오게 됩니다.

 

그리고 이를 표현하기 위해서 make_grid 함수를 이용해서 grid 이미지를 만들어주고, 이것을 writer.add_image를 통해 tensorboard에 그려줍니다.

 

def latent_to_image(epoch, model):
    with torch.no_grad():
        sample = torch.randn(64, 2).to(DEVICE)
        recon_image = model.decode(sample).cpu()
        grid = torchvision.utils.make_grid(recon_image.view(64, 1, 28, 28))
        writer.add_image("Latent To Image", grid, epoch)

 

latent_to_image는 latent variable을 이미지로 만들어주는 함수입니다.

 

여기에서는 gradient를 계산하지 않으므로 torch.no_grad()를 먼저 선언해줍니다.

 

torch.randn(64, 2)으로 64개의 2차원짜리 랜덤 값들을 만들어냅니다.

 

그리고 이 값을 model.decode를 통해서 reconstruction 이미지를 만들어줍니다.

 

reconstruction 된 이미지를 grid 이미지로 만들어주고, 이를 또다시 writer.add_image를 사용해서 tensorboard에 그려줍니다.

 

해당 함수를 통해서 평균 0, 분산 1인 Gaussian distribution을 가지는 데이터가 주어졌을 때, 어떻게 이미지로 복원하는지를 확인할 수 있습니다.

 

논문에서 Decoder라고 부르던 $p_\theta(x|z)$ 부분이 잘 기능하는지를 확인해보는 것이라고 보시면 되겠습니다.

 

for epoch in tqdm(range(0, EPOCHS)):
    train(epoch, VAE_model, trainloader, optimizer)
    test(epoch, VAE_model, testloader)
    print("\n")
    latent_to_image(epoch, VAE_model)

writer.close()

얼마나 남았는지 확인해주기 위해서 tqdm을 달아주고, range(0, EPOCHS)를 지정해서 총 50 epochs 동안 학습이 진행되도록 해줍니다.

 

train (VAE 모델 학습) => test (VAE 모델이 잘 복원하는지를 확인) => latent_to_image (잠재 변수가 주어졌을 때 image generation을 잘하는지 확인)을 해주고, epoch을 다 돌면 writer.close()를 통해 tensorboard에 써주는 writer를 닫아줍니다.

 

 

%load_ext tensorboard

%tensorboard --logdir='/content/drive/MyDrive/VAE_Result/2021-03-15-15:39'

해당 코드는 Google colab에서 사용할 때 적용하는 코드입니다.

 

그리고 해당 경로는 제가 돌린 결과를 저장한 폴더의 위치라고 보시면 되겠습니다.

 

다음으로는 해당 코드를 돌렸을 때 얻게 되는 결과들에 대해서 살펴보겠습니다.

 

먼저 Train입니다.

 

Total Loss = KL-Divergence + Reconstruction Error로 계산되며, Reconstruction Error는 감소하고 있고 KL-Divergence는 계속해서 증가하는 모습을 보이고 있습니다.

 

Total Loss 관점에서는 계속해서 떨어지고 있네요.

 

Reconstruction Error가 감소하는 것을 보면, 기존 이미지를 잘 구현해나가고 있구나 라고 생각해볼 수 있습니다.

 

하지만, KL-Divergence가 계속해서 증가하는 모습을 보이고 있는데, 이는 $q_\phi(z|x^{(i)})$가 $p_\theta(z)$와 가까워지지 못하고 있다는 사실을 알 수 있습니다. 

 

논문에서 KL-Divergence term이 결국 $\phi$를 regularization 하는 역할이라고 했었는데, Encoder의 parameter들이 적절하게 학습되지 못하고 있는 것 같습니다.

 

 

Test에서도 크게 다르지 않은 모습을 보이고 있습니다.

 

여전히 KL-Divergence는 증가하고 있고, Reconstruction Error는 감소하여 Total Loss는 감소하고 있는 모습을 보입니다.

 

 

다음으로는 이미지들을 살펴보겠습니다.

 

 

위에 3가지 사진은, Test image가 주어졌을 때 실제 Test image 8개와(위쪽) 이를 model의 input으로 투입했을 때 얻게 되는 reconstruction image 8개를 보여줍니다.

 

 

첫 번째는 0 epoch일 때, 두 번째는 23 epoch일 때, 세 번째는 49 epoch일 때입니다. (사진에서 보이는 오렌지색 동그라미를 움직이면 해당하는 epoch의 이미지를 볼 수 있습니다. interactive 한 화면이라서 처음 중간 끝 정도의 3가지만 보여드립니다.) 

 

 

생각보다는 엄청 깔끔하게 생성하는 것 같지는 않습니다.

 

 

다음으로는 latent variable이 제공되었을 때, 어떻게 이미지를 generation 하는지를 살펴보겠습니다.

 

 

맨 처음 단계에서는 알 수 없는 이미지들이 대부분이지만, 갈수록 원래 데이터에서 보일법한 이미지들이 뚜렷하게 보입니다.

 

엄청 깔끔하진 않지만, 대부분 조금 blur하나 그래도 이게 어떤 숫자인지 인지할 수 있을 정도의 퀄리티는 나오고 있네요.

 

 

위에서 실행했던 코드들을 보고 싶으시다면 아래 주소의 제 깃헙으로 와주시면 됩니다.

 

 

github.com/PeterKim1/paper_code_review

 

 

 

여기까지 Auto-Encoding Variational Bayes(VAE)의 code review를 마치겠습니다.

 

 

감사합니다.

 

 

 

 

 

 

 

 

 

 

 

두 번째로 다뤄볼 논문은 VAE라는 이름으로 잘 알려진 Auto-Encoding Variational Bayes라는 논문입니다.

 

 

너무 유명한 논문이라 다양한 자료들이 많이 있지만, 가급적이면 다른 분들이 가공해서 만든 자료들의 열람은 피하고 논문에 있는 내용만을 토대로 최대한 이해해보는 쪽으로 시도하였습니다.

 

 

시작해보겠습니다.

 

 

Abstract

 

 

큰 데이터셋과 계산이 불가능한 posterior 분포를 가지는 연속형 잠재 변수를 가지고 있을 때, 어떻게 directed probabilistic model을 효율적으로 학습하고 추론할 수 있을까?

 

우리는 큰 데이터셋에도 확장할 수 있고 가벼운 미분가능성 조건이 있다면 계산이 불가능한 경우에도 작동하는 stochastic variational inference and learning 알고리즘을 제안한다.

 

우리의 기여는 두 가지이다.

 

첫 번째, variational lower bound의 reparameterization이 표준적인 stochastic gradient 방법론들을 사용하여 직접적으로 최적화될 수 있는 lower bound estimator를 만들어낸다는 것을 보였다.

 

두 번째, 각 datapoint가 연속형 잠재 변수를 가지는 i.i.d. 데이터셋에 대해서, 제안된 lower bound estimator를 사용해 approximate inference model(또는 recognition model이라고 불림)을 계산이 불가능한 posterior에 fitting 시킴으로써 posterior inference가 특히 효율적으로 만들어질 수 있다는 점을 보인다. 실험 결과에 이론적 이점이 반영되었다.

 

 

 

1. Introduction

 

 

연속적인 잠재 변수 및/또는 매개 변수가 계산하기 어려운 사후 분포를 갖는 directed probabilistic model을 가지고 어떻게 하면 효율적인 approximate inference와 learning을 수행할 수 있을까?

 

Variational Bayesian (VB) 접근법은 계산 불가능한 posterior로의 근사의 최적화를 포함한다.

 

불행하게도, 일반적인 mean-field 접근법은 근사적인 posterior에 대한 기댓값의 분석적 해를 요구하며, 일반적인 경우에 이 또한 계산 불가능하다.

 

우리는 variational lower bound의 reparameterization이 어떻게 lower bound의 미분 가능한 unbiased estimator를 만들어내는지를 보인다.

 

이 SGVB (Stochastic Gradient Variational Bayes) estimator는 연속형 잠재 변수나 파라미터를 가지는 어떤 모델에서도 효율적인 approximate posterior inference를 위해 사용될 수 있으며, 표준 gradient ascent 기법을 사용해서 직접적으로 최적화한다. (approximate posterior inference란, posterior를 직접적으로 계산할 수 없기 때문에 근사적인 방법으로 구하는 것을 의미합니다. 딥러닝에서의 inference와는 차이가 있습니다.)

 

각 datapoint가 연속형 잠재 변수를 가지는 i.i.d. 데이터셋의 경우에, 우리는 Auto-Encoding VB (AEVB) 알고리즘을 제안한다.

 

AEVB 알고리즘에서, 우리는 단순한 ancestral sampling을 사용하여 매우 효율적인 approximate posterior inference를 수행하게 해주는 recognition model을 최적화하기 위해 SGVB estimator를 사용함으로써 추론과 학습을 특히 효율적으로 만들 수 있으며, 이는 각 datapoint에 MCMC와 같은 expensive 한 반복적 추론 방법 없이도 모델의 파라미터들을 효율적으로 학습할 수 있도록 해준다. (여기서 expensive 하다는 의미는 연산 관점에서 연산량이 많다는 의미입니다.)

 

학습된 approximate posterior inference model은 recognition, denoising, representation, visualization와 같은 목적을 위해 사용될 수 있다.

 

Recognition model에 neural network가 사용되었을 때, 우리는 variational auto-encoder에 도달한다.

 

 

 

2. Method

 

 

 

이번 section에서의 전략은 연속형 잠재 변수를 가지고 있는 다양한 directed graphical model을 위한 lower bound estimator (a stochastic objective function)을 도출하는 데 사용될 수 있다.

 

우리는 각 datapoint가 잠재 변수를 가지는 i.i.d 데이터셋이 존재하는 일반적인 경우로만 제한할 것이며, 파라미터들에 대해서는 maximum likelihood (ML)이나 maximum posteriori (MAP) 추론을 진행하고 잠재 변수에 대해서는 variational inference를 수행한다.

 

예를 들어서 이 시나리오를 우리가 variational inference를 global parameters에 수행하는 경우로 확장하는 것은 간단하며, 이는 appendix에 들어있고 이 케이스에 해당하는 실험은 future work로 남긴다.

 

우리의 방법은 streaming data와 같은 online- non-stationary setting에도 적용할 수 있으나, 단순함을 위해 고정된 데이터셋을 가정한다.

 

 

Figure 1: 우리가 고려하는 directed graphical model의 유형을 나타낸다. 실선은 generative model $p_\theta(z)p_\theta(x|z)$이며, 점선은 계산 불가능한 posterior $p_\theta(z|x)$로의 variational approximation $q_\phi(z|x)$를 나타낸다. variational parameters $\phi$는 generative model parameters $\theta$와 함께 학습된다.

 

 

2.1 Problem scenario

 

 

 

연속형 변수 혹은 이산형 변수 $x$의 $N$개의 i.i.d. sample로 구성된 데이터셋 $X = \{x^{(i)}\}^N_{i=1}$을 고려하자.

 

관측되지 않은 연속형 랜덤 변수 $z$를 포함하는 어떤 random process에 의해서 데이터가 생성되었다고 가정하자.

 

Process는 2개의 step으로 구성된다.

 

(1) $z^{(i)}$는 어떤 사전 분포 $p_{\theta^*}(z)$로부터 생성되었다.

 

(2) $x^{(i)}$는 어떤 조건부 분포 $p_{\theta^*}(x|z)$로부터 생성되었다.

 

우리는 prior $p_{\theta^*}(z)$와 likelihood $p_{\theta^*}(x|z)$가 parametric families of distribution $p_\theta(z)$와 $p_\theta(x|z)$로부터 왔다고 가정하며, 그들의 PDF는 $\theta$와 $z$에 대해서 거의 모든 곳에서 미분 가능하다고 가정한다.

 

불행하게도, 우리의 관점에서 이 과정의 많은 것들이 숨겨져 있다: 즉, true parameters $\theta^*$와 잠재 변수들의 값 $z^{(i)}$은 우리에게 알려져 있지 않다.

 

매우 중요하게, 우리는 주변 확률이나 사후 확률에 대해서 일반적인 단순화한 가정을 만들지 않는다.

 

대조적으로, 우리는 이러한 경우에서도 효율적으로 작동하는 일반적인 알고리즘에 관심이 있다.

 

1. Intractability: marginal likelihood의 적분 $p_\theta(x) = \int p_\theta(z)p_\theta(x|z)dz$이 계산 불가능한 경우(따라서 우리는 marginal likelihood를 평가하거나 미분할 수 없다)를 말하며, true posterior density $p_\theta(z|x) = p_\theta(x|z)p_\theta(z)/p_\theta(x)$도 계산 불가능하며(따라서 EM algorithm을 사용할 수 없음), 어떤 합리적인 mean-field VB algorithm을 위해 요구되는 적분도 계산 불가능한 경우를 말한다.

 

이러한 계산 불가능성은 꽤 흔하고 nonlinear hidden layer를 포함하는 신경망과 같은 적당히 복잡한 likelihood function $p_\theta(x|z)$의 경우에서 나타난다. (즉, posterior를 적분과 같은 계산을 통해서 구할 수 없는 경우에도 알고리즘이 작동해야 한다는 말입니다. marginal likelihood의 적분식을 보면, $z$에 대해서 적분을 시행하게 되는데 우리는 $z$에 대해서 알지 못하기 때문에 이를 실제 적분을 시행할 수 없습니다.)

 

2. A large dataset: 우리는 너무 많은 데이터를 가지고 있어서 batch optimization은 너무 연산량이 많다. 우리는 small minibatch나 심지어 하나의 datapoints만 사용해서 parameter update를 하고 싶다.

 

Monte Carlo EM과 같은 Sampling 기반의 솔루션은 일반적으로 매우 느린데, 이는 datapoint마다 전형적으로 연산량이 많은 샘플링 loop를 포함하기 때문이다.

 

 

우리는 위의 시나리오에서 3개의 관련된 문제들에 관심이 있으며, 이에 대한 해결책을 제안한다.

 

 

1. Parameters $\theta$에 대한 Efficient approximate ML or MAP 추정. 예를 들어서, natural process를 분석하는 경우와 같이 매개 변수 자체에 관심이 있을 수 있다. 그들은 또한 우리가 숨겨진 random process를 모방하도록 해주며 real data를 닮은 인공 데이터를 생성하게 해 준다.

 

2. Parameter $\theta$의 선택을 위한 관측된 값 $x$가 주어졌을 때 잠재 변수 $z$에 대한 효율적인 approximate posterior inference. 이는 coding이나 data representation task에 유용하다.

 

3. 변수 $x$의 효율적인 approximate marginal inference. 이는 우리가 $x$에 대한 prior가 요구되는 모든 종류의 inference task를 수행할 수 있도록 한다. computer vision에서의 일반적인 응용 사례는 image denoising, inpainting, super-resolution을 포함한다.

 

 

위의 문제들을 해결하기 위해, recognition model $q_\phi(z|x)$를 도입한다. 이는 계산 불가능한 true posterior $p_\theta(z|x)$에 대한 추정이다. 

 

Mean-field variational inference에서의 approximate posterior와는 대조적으로, 이는 반드시 factorial일 필요는 없으며 parameters $\phi$는 closed-form expectation으로부터 계산되지 않음을 유의한다.

 

그 대신에, 우리는 생성 모델 파라미터 $\theta$와 recognition model 파라미터 $\phi$를 동시에 학습하는 방법을 도입한다.

 

 

Coding theory 관점에서, 관측되지 않은 변수 $z$는 latent representation혹은 code라는 해석을 가지고 있다.

 

이번 논문에서, 우리는 그러므로 recognition model $q_\phi(z|x)$를 확률적 encoder로 지칭하며, 이는 datapoint $x$가 주어졌을 때 이 모델이 datapoint $x$가 생성될 수 있는 지점인 code $z$의 가능한 값들에 대한 분포(예를 들어, Gaussian 분포)를 만들어 내기 때문이다.

 

유사한 방식으로, 우리는 $p_\theta(x|z)$를 확률적 decoder로 지칭할 것이며, code $z$가 주어졌을 때 이는 가능한 $x$의 값들에 대한 분포를 만들어낸다.

 

 

 

 

 

2.2 The Variational Bound

 

 

 

Marginal likelihood는 각각의 datapoint들의 marginal likelihood의 합으로 구성된다.

 

즉, $logp_\theta(x^{(1)}, ..., x^{(N)})$ = $\sum^N_{i=1}logp_\theta(x^{(i)})$이며, 이는 다음과 같이 다시 쓰일 수 있다.

 

 

우변의 첫 번째 항은 true posterior와의 approximate 간의 KL divergence이다. (KL divergence란, GAN paper에서도 봤지만 두 분포의 차이를 계산하는 방법입니다. 위의 식에서 true posterior가 $p_\theta(z|x^{(i)})$를 의미하고, approximate가 $q_\phi(z|x^{(i)})$를 의미해요. approximate는 위에서 Recognition model, 혹은 확률적 Encoder라는 이름으로도 설명되었습니다. )

 

KL-divergence가 비음(non-negative) 이므로, 우변의 두 번째 항 $L(\theta, \phi; x^{(i)})$는 datapoint $i$의 대한 marginal likelihood에 대한 (variational) lower bound이다. 이는 다음과 같이 쓰일 수 있다.

 

 

이는 다음과 같이 쓰일 수 있다.

 

우리는 variational parameters $\phi$와 generative parameters $\theta$ 둘 다에 대해서 lower bound $L(\theta, \phi;x^{(i)})$를 미분하고 최적화하고 싶다. 

 

하지만, lower bound의 $\phi$에 대한 gradient는 다소 문제가 있다.

 

이런 종류의 문제에 대한 일반적인 Monte Carlo gradient estimator는

이며, $z^{(l)} \sim q_\phi(z|x^{(i)})$이다. 

 

이러한 gradient estimator는 매우 높은 variance를 보이고, 우리의 목적에는 실용적이지 않다.

 

 

 

2.3 The SGVB estimator and AEVB algorithm

 

 

 

이번 section에서 우리는 the lower bound와 파라미터에 대한 lower bound의 미분 값에 대한 실용적 estimator를 소개한다.

 

approximate posterior를 $q_\phi(z|x)$의 형태로 가정하지만, 이 기술은 $q_\phi(z)$의 경우에도 적용될 수 있다.

 

즉, $x$에 대한 조건부가 아닐 때도 가능하다는 의미이다.

 

주어진 parameters에 대한 posterior를 추론하는 fully variational Bayesian method는 appendix에 쓰여있다.

 

 

Section 2.4에서 서술된 어떤 가벼운 조건 하에서 주어진 approximate posterior $q_\phi(z|x)$에 대해 우리는 random variable $\tilde{z} \sim q_\phi(z|x)$를 (보조) noise variable $\epsilon$의 미분 가능한 transformation $g_\phi(\epsilon, x)$를 사용하여 reparameterize 할 수 있다.

 

 

적절한 distribution $p(\epsilon)$과 function $g_\phi(\epsilon, x)$를 선택하는 것에 대한 일반적인 전략은 section 2.4에서 확인할 수 있다.

 

우리는 이제 $q_\phi(z|x)$에 대한 어떠한 함수 $f(z)$의 기댓값에 대한 Monte Carlo estimate를 구성할 수 있다. (기댓값을 직접 구하기 어렵기 때문에, Monte Carlo 기법을 활용해서 추정하는 것이라고 보면 될 것 같습니다.)

 

 

우리는 이 기술을 variational lower bound (식 (2))에 적용하여 이를 통해 generic Stochastic Gradient Variational Bayes (SGVB) estimator $\tilde{L^A}(\theta, \phi; x^{(i)}) \simeq L(\theta, \phi; x^{(i)})$를 만들 수 있다.

(논문에 쓰여있는 그대로, Monte Carlo estimate를 식 (2)에 적용하면 식 (6)을 도출할 수 있습니다.)

 

 

종종, 식 (3)의 KL-divergence $D_{KL}(q_\phi(z|x^{(i)}) \parallel p_\theta(z))$는 분석적으로 통합될 수 있으며(appendix B를 참조), expected reconstruction error $E_{q_\phi(z|x^{(i)})}[logp_\theta(x^{(i)} | z)]$는 샘플링에 의한 추정이 요구된다.

 

KL-divergence는 $\phi$를 규제하는 것으로 해석될 수 있으며, approximate posterior가 prior $p_\theta(z)$에 가까워지도록 유도한다.

 

이는 두 번째 버전의 SGVB estimator $\tilde{L^B}(\theta, \phi; x^{(i)}) \simeq L(\theta, \phi; x^{(i)})$를 만들어내며, 이는 식 (3)에 대응되고, generic estimator(식 (6) 번)에 비해서 일반적으로 더 낮은 variance를 가진다.

 

 

$N$ data point를 가지는 dataset $X$로부터 여러 개의 datapoints가 주어질 때, 미니 배치를 기반으로 전체 데이터셋의 marginal likelihood lower bound의 estimator를 만들 수 있다.

 

 

Minibatch $X^M = \left\{x^{(i)}\right\}^M_{i=1}$은 $N$ data point를 가지는 전체 데이터셋 $X$로부터 $M$개의 datapoints가 랜덤 하게 뽑힌 것이다.

 

우리 실험에서, datapoint 당 샘플의 수인 $L$은 1로 지정할 수 있으며, 그동안 minibatch size $M$은 충분히 커야 한다. 예를 들어, $M$ = 100 정도는 되어야 한다.

 

미분 값 $\triangledown_{\theta, \phi}\tilde{L}(\theta; X^M)$는 얻어질 수 있고, 결과로 나오는 gradient는 SGD나 Adagrad와 같은 stochastic optimization emthod와 결합되어 사용될 수 있다.

 

Stochastic gradient를 계산하기 위한 기초적인 접근법이 algorithm 1에 나와있다.

 

 

Auto-encoders와의 연결은 식 (7)에 나타난 objective function을 봤을 때 명확해진다. 

 

prior로부터 approximate posterior와의 KL divergence인 첫 번째 항은 regularizer의 역할을 하게 되며, 두 번째 항은 expected negative reconstruction error이다.

 

함수 $g_\phi(.)$은 datapoint $x^{(i)}$와 random noise vector $\epsilon^{(l)}$를 해당 datapoint에 대한 approximate posterior로부터 나온 샘플로 맵핑을 한다.

 

즉, $z^{(i, l)} = g_\phi(\epsilon^{(l)}, x^{(i)})$이고 $z^{(i, l)} \sim q_\phi(z|x^{(i)})$이다. 

 

그 결과로, sample $z^{(i, l)}$는 함수 $logp_\theta(x^{(i)} | z^{(i, l)})$의 input이 되며, 이는 $z^{(i, l)}$가 주어졌을 때, generative model 하에서 datapoint $x^{(i, l)}$의 확률 밀도(혹은 질량)와 같다. 이 항은 auto-encoder에서 negative reconstruction error이다.

 

 

 

2.4 The reparameterization trick

 

 

 

우리의 문제를 해결하기 위해, $q_\phi(z|x)$로부터 샘플을 생성해내기 위한 대안적인 방법을 적용했다.

 

본질적인 parameterization trick은 꽤 단순하다.

 

$z$가 연속적인 랜덤 변수라고 하고, $z \sim q_\phi(z|x)$는 어떤 조건부 분포라고 하자.

 

그러고 나서 랜덤 변수 $z$를 deterministic 변수 $z = g_\phi(\epsilon, x)$로 표현하는 것이 가능하며, $\epsilon$은 독립적인 주변 분포 $p(\epsilon)$에서 나온 보조 변수이며, $g_\phi(.)$은 $\phi$에 의해서 parameterized 된 vector-valued 함수이다.

 

이러한 reparameterization은 $q_\phi(z|x)$에 대한 기댓값을 재작성하는 데 사용될 수 있기 때문에 우리의 경우에 유용하며, 이러한 기댓값의 Monte Carlo estimate는 $\phi$와 관련하여 미분 가능하게 될 수 있다.

 

증명은 다음과 같다.

 

Deterministic mapping $z = g_\phi(\epsilon, x)$가 주어졌을 때, $q_\phi(z|x)\prod_idz_i$ $=$ $p(\epsilon)\prod_{i} d\epsilon_i$ 라는 사실을 알고 있다.

 

그러므로, $\int q_\phi(z|x)f(z)dz = \int p(\epsilon)f(z)d\epsilon = \int p(\epsilon)f(g_\phi(x, \epsilon^{(i)}))d\epsilon$ 이다. 

 

section 2.3에서 우리는 이 trick을 variational lower bound의 미분 가능한 estimator를 얻기 위해 적용했다.

 

예를 들어서, univariate Gaussian case를 생각해보면, $z \sim p(z|x) = N(\mu, \sigma^2)$이다.

 

이 경우에서는, 유효한 reparameterization은 $z = \mu + \sigma\epsilon$이며, $\epsilon$은 $\epsilon \sim N(0, 1)$을 만족하는 보조 노이즈 변수이다.

 

그러므로

를 만족한다.

 

 

어떤 $q_\phi(z|x)$에 대해서, 우리는 미분 가능한 transformation $g_\phi(.)$과 보조 변수 $\epsilon \sim p(\epsilon)$을 선택할 수 있을까? 3가지 기초적인 접근법은 다음과 같다.

 

1. 계산 가능한 inverse CDF. 이 경우에는, $\epsilon \sim u(0, I)$라 하고, $g_\phi(\epsilon, x)$를 $q_\phi(z|x)$의 inverse CDF라고 하자. 예시: Exponential, Cauchy, Logistic, Rayleigh, Pareto, Weibull, Reciprocal, Gompertz, Gumbel and Erlang 분포가 될 수 있다.

 

2. Gaussian 예시와 유사하게, 어떠한 "location-salce" 계통의 분포를 보조 변수 $\epsilon$의  standard distribution(location =0, scale = 1)으로 선택할 수 있으며, $g(.)$ = location + scale $\cdot \epsilon$로 놓는다. 예시: Laplace, Elliptical, Student's t, Logistic, Uniform, Triangular and Gaussian distribution.

 

3. 랜덤 변수를 보조 변수들의 다른 transformation으로 표현할 수 있다. 예시: Log-Normal(normal하게 분포된 변수의 exponentiation), Gamma(exponentially 하게 분포된 변수들에 대한 합), Dirichlet(Gamma variates의 가중 합), Beta, Chi-Squared, and F 분포.

 

모든 세 접근법이 실패했을 때, inverse CDF에 대한 좋은 근사가 존재하면 PDF에 비교될 정도의 시간 복잡도가 요구된다.

 

 

 

3. Example: Variational Auto-Encoder

 

 

 

이번 section에서 확률적 encoder $q_\phi(z|x)$(generative model $p_\theta(x, z)$의 posterior에 대한 근사)로 신경망을 사용했을 때의 예시를 보여주며, parameter $\phi$와 $\theta$가 AEVB algorithm을 가지고 동시에 최적화되는 예시를 보여준다.

 

잠재 변수에 대한 prior를 centered isotropic multivariate Gaussian $p_\theta(z) = N(z; 0, I)$라고 하자.  이런 경우에 prior는 parameter가 없다는 것을 알아두자. 

 

우리는 $p_\theta(x|z)$를 실수 데이터의 경우에 multivariate Gaussian으로, binary data의 경우 Bernoulli로 놓으며 이 분포의 파라미터들은 MLP(하나의 hidden layer를 가지는 fully-connected 신경망)를 가지고 $z$로부터 계산될 수 있다.

 

True posterior $p_\theta(z|x)$는 이 경우에 계산이 불가능하다는 것을 알아두자.

 

반면에, $q_\phi(z|x)$의 형태에는 많은 자유가 있으며, 우리는 true (but intractable) posterior가 approximately diagonal covariance를 가지는 approximate Gaussian을 맡는다고 가정한다. 

 

이 경우에, 우리는 variational approximate posterior를 diagonal covariance structure를 가지는 multivariate Guassian으로 정할 수 있다.

 

 

Approximate posterior의 평균과 표준편차인 $\mu^{(i)}$와 $\sigma^{(i)}$는 datapoint $x^{(i)}$와 variational parameter $\phi$을 가지는 비선형 함수인 encoding MLP의 output이다. (appendix C 참조)

 

Section 2.4에서 설명했던 대로, 우리는 $\epsilon^{(l)} \sim N(0, I)$일 때 $z^{(i, l)} = g_\phi(x^{(i)}, \sigma^{(i)}) = \mu^{(i)} + \sigma^{(i)} \circledcirc \epsilon^{(l)}$을 사용하여 $z^{(i, l)} \sim q_\phi(z|x^{(i)})$로부터 샘플링을 진행한다.

 

$\circledcirc$는 element-wise product를 나타낸다.

 

이 모델에서 $p_\theta(z)$ (the prior)와 $q_\phi(z|x)$는 둘 다 Gaussian이다; 이 경우에, 우리는 식 (7)의 estimator를 사용할 수 있으며 추정 없이 KL divergence가 계산되고 미분될 수 있다.

 

모델에 대한 그 결과로의 estimator와 datapoint $x^{(i)}$는 다음과 같다.

 

appendix C와 위에서 설명한 대로, decoding term $logp_\theta(x^{(i)} | z^{(i, l)})$는 Bernoulli나 Gaussian MLP이며, 우리가 모델링하려는 데이터의 유형에 의존한다.

 

 

4. Related work와 5. Experiment는 생략하였습니다.

 

 

 

6. Conclusion

 

 

우리는 연속형 잠재 변수를 효율적으로 approximate inference 하기 위한 새로운 variational lower bound의 estimator인 Stochastic Gradient VB (SGVB)를 소개했다. 제안된 estimator는 단도직입적으로 미분될 수 있고 standard stochastic gradient method를 사용해 최적화될 수 있다. 

 

각 datapoint가 연속형 잠재 변수를 가지는 i.i.d dataset의 경우에, 우리는 효율적인 추론과 학습이 가능한 효율적인 알고리즘인 Auto-Encoding VB (AEVB)를 소개했으며, SGVB estimator를 사용하여 approximate inference model을 학습한다.

 

 

7. Future work

 

 

SGVB estimator와 AEVB algorithm이 연속형 잠재 변수를 가지는 어떤 추론 문제나 어떤 학습 문제에도 적용될 수 있기 때문에 많은 미래 연구 방향이 존재한다.

 

(i) AEVB와 공동으로 학습한 인코더와 디코더에 사용되는 neural network (예: convolutional networks)을 가진 계층적 생성 architecture를 학습하는 것

 

(ii) dynamic Bayesian networks와 같은 시계열 모델

 

(iii) SGVB의 global parameters로의 응용

 

(iv) 잠재 변수를 이용한 supervised models, 이는 복잡한 노이즈 분포를 학습하는데 유용하다.

 

 

 

수식들도 너무 많고, 이해하기가 쉽지 않은 논문이라서 정리하는데 꽤 오랜 시간이 걸렸습니다.

 

 

기존에는 논문을 좀 세세하게 보는 것을 목표로 하려고 했는데, VAE를 읽다 보니 이게 진짜 효율적인가 하는 의문이 드네요 ㅠㅠ

 

 

다음 글에서는 VAE가 코드로 구현되었을 때 어떻게 구현되는지에 대해서 다루도록 하겠습니다.

 

 

논문이 이렇게 수식적으로 어려운데 비해서, 사실 코드로 구현하는 것 자체는 간단하다고 생각합니다.

 

 

대부분의 수식들이 전개하거나 정리하는 과정에서 도출되는 것들이라.....

 

 

 

 

Generative Adversarial Nets(GAN) 논문 리뷰: cumulu-s.tistory.com/22

 

1. Generative Adversarial Nets(GAN) - paper review

안녕하세요. 새롭게 (paper + code) review라는 항목을 만들었고, 여기에 하나하나 글을 채워나갈 예정입니다. 블로그 글에는 논문의 내용을 조금 더 디테일하게 정리하면서 나름대로 저의 생각을 얹

cumulu-s.tistory.com

 

이전 글에서는, Generative Adversarial Nets(GAN) 논문에 대해서 상세하게 정리해보았습니다.

 

 

이번 글에서는, 직접 코드를 하나하나 짜 보면서 논문에 나온 내용들이 어떻게 구현될 수 있는지를 확인해보겠습니다.

 

 

저는 Deep learning library 중 pytorch를 메인으로 사용하고 있어서, pytorch로 작성하였음을 알립니다.

 

 

그럼 시작해보겠습니다.

 

 

# Import packages
import torch
import torchvision
import torchvision.transforms as transforms
import torch.nn as nn
import torch.optim as optim
from tqdm.auto import tqdm
import numpy as np
import matplotlib.pyplot as plt

먼저 필요한 패키지들을 불러옵니다. torch와 torchvision, numpy 등을 불러옵니다.

 

 

tqdm의 경우, for문이 얼만큼 돌았는지 나타내 주는 패키지로 여러 번의 반복문을 돌아야 하는 코드에서 유용하게 사용되는 패키지입니다.

 

 

USE_CUDA = torch.cuda.is_available()
DEVICE = torch.device("cuda" if USE_CUDA else "cpu")
print("사용하는 Device : ", DEVICE)

EPOCHS = 400
BATCH_SIZE = 200

torch.cuda.is_avilable()은 cuda를 사용할 수 있는지를 True / False로 알려줍니다. 즉 GPU를 사용할 수 있는지 확인하는 코드입니다.

 

DEVICE는 gpu가 가능하면 cuda로, 아니면 cpu로 뜨게 만들어줍니다.

 

그리고 학습을 진행할 에폭과 batch size를 지정해줍니다. 

 

batch size의 경우 Dataloader에서 나오는 데이터의 수를 결정하므로 여기서 먼저 지정해줍니다.

 

# code for MNIST dataset loading error at Google Colab.
from six.moves import urllib    
opener = urllib.request.build_opener()
opener.addheaders = [('User-agent', 'Mozilla/5.0')]
urllib.request.install_opener(opener)

해당 코드는, 혹시나 Google Colab에서 해당 코드를 돌리시는 분들을 위해 작성된 코드입니다.

 

Google Colab을 사용하지 않으신다면 넘어가셔도 좋습니다.

 

현재 torchvision에서 MNIST dataset을 불러올 때, 데이터셋 링크로부터 불러오는 코드가 거절당하는 경우가 있어 이를 세팅해주는 코드입니다.

 

# Transformer code
transformer = transforms.Compose([
            transforms.ToTensor(),
            transforms.Normalize((0.5,), (0.5,))
])


# Loading trainset, testset and trainloader, testloader
trainset = torchvision.datasets.MNIST(root = '/content/drive/MyDrive/MNIST', train = True,
                                        download = True, transform = transformer)

trainloader = torch.utils.data.DataLoader(trainset, batch_size = BATCH_SIZE, shuffle = True, num_workers = 2)


testset = torchvision.datasets.MNIST(root = '/content/drive/MyDrive/MNIST', train = False,
                                        download = True, transform = transformer)

testloader = torch.utils.data.DataLoader(testset, batch_size = BATCH_SIZE, shuffle = True, num_workers = 2)

transformer는 데이터셋을 받아서 변형해주는 도구입니다.

 

classification과 같은 task를 할 때는 여기에 Augmentation을 넣어주기도 합니다. 

 

transforms.ToTensor()는 numpy array를 torch tensor로 바꿔주는 역할을 합니다. 

 

보통 데이터셋들은 numpy array로 되어 있고, 이를 pytorch에서 사용하려면 torch tensor의 형태로 변환해줘야 합니다.

 

transforms.Normalize는 정규화를 해주는 코드입니다.

 

정규화를 진행하지 않으면 MNIST 데이터셋이 0부터 1의 값을 가지도록 조정이 되어있습니다.

 

따라서, 이에 평균 0.5, 표준편차 0.5로 정규화를 진행해줍니다.

 

정규화는 $\frac{x-\mu}{\sigma}$의 형태로 진행됩니다.

 

따라서 0의 값은 -1이 되고, 1의 값은 1이 됩니다. 이 과정을 통해 MNIST 데이터셋이 -1부터 1의 값을 가지도록 바꿔줍니다.

 

torchvision.datasets.MNIST를 통해서 MNIST 데이터셋을 받을 수 있고, root는 데이터셋을 받을 경로입니다. 

 

해당 경로는 제가 사용하고 있는 경로이므로, 직접 사용하실 때는 이 부분을 원하시는 경로로 변경해주셔야 합니다.

 

다음으로는 torch.utils.data.DataLoader를 정의해줍니다. DataLoader는 데이터 전체를 보관하고 있는 일종의 container 같은 것으로, 이를 통해 데이터셋 전체를 메모리에 올리지 않아도 되게 만들어줍니다.

 

즉, batch size만큼만 DataLoader에서 데이터를 내보내주는 방식을 사용하는 것이죠.

 

# sample check
sample, label = next(iter(trainloader))

# show grid image
def imshow_grid(img):
    img = torchvision.utils.make_grid(img.cpu().detach())
    img = (img + 1) / 2
    npimg = img.numpy()
    plt.imshow(np.transpose(npimg, (1, 2, 0)))
    ax = plt.gca()
    ax.axes.xaxis.set_visible(False)
    ax.axes.yaxis.set_visible(False)
    plt.show()


imshow_grid(sample[0:8])

 

해당 코드는, DataLoader로부터 데이터가 잘 나오고 있는지를 확인하는 코드입니다.

 

iter()를 통해서 trainloader를 iterator로 만들어주고, next()를 이용해 한 번 데이터를 뽑도록 만들어줍니다.

 

현재 mnist trainloader는 이미지 데이터와 label을 동시에 뱉어내기 때문에, sample , label의 형태로 두 개의 변수를 지정해줘야 합니다.

 

imshow_grid 함수는 이미지를 받아서 이를 grid 형태로 보여주는 함수입니다.

 

torchvision.utils.make_grid()를 이용하면 grid 형태의 이미지를 만들 수 있습니다.

 

여기서 (img + 1) / 2를 적용해주는 이유는, 우리가 0 ~ 1로 되어 있는 데이터를 -1 ~ 1로 만들어줬기 때문입니다.

 

따라서 여기에 다시 1을 더해주고, 2로 나눠주어 원래의 0 ~ 1 형태로 원상복구 해주기 위함입니다.

 

그리고 현재는 데이터셋이 torch tensor로 되어 있으므로, 이를 numpy()를 이용하여 다시 numpy array로 만들어줘야 합니다.

 

그리고 np.transpose를 사용해주는 이유는, mnist 데이터셋은 (channel, width, height) 형태의 shape를 가지고 있기 때문입니다.

 

따라서, 실제로 이를 plt.imshow()를 통해서 시각화하려면 차원의 순서를 바꿔줘야 합니다. 그래서 사용하는 것이고요.

 

이 코드를 통해 아래에 보이는 그림은 8개의 샘플만 뽑아서 시각화를 진행한 결과입니다.

 

# Discriminator class
class Dis_model(nn.Module):
    def __init__(self, image_size, hidden_space):
        super(Dis_model, self).__init__()
        self.features = nn.Sequential(
            nn.Linear(image_size, hidden_space),
            nn.ReLU(),
            nn.Linear(hidden_space, hidden_space),
            nn.ReLU(),
            nn.Linear(hidden_space, 1),
            nn.Sigmoid())
    
    def forward(self, input_x):
        x = self.features(input_x)
        return x

다음으로는 Discriminator class를 만들어주었습니다.

 

보통은 모델을 class형태로 만들어주기 때문에, 비록 GAN 모델 구현은 그리 복잡하진 않아서 이렇게 하지 않고 더 간단하게도 짤 수 있겠지만 그냥 습관적으로 class로 만들어보았습니다.

 

image size를 지정해주면, 이를 입력으로 받아서 hidden space 만큼의 fully connected layer를 만들어주고, 다시 hidden space - hidden space 만큼의 fully connected layer를 만들어준 다음, 마지막으로는 output이 1로 나오도록 해줍니다.

 

이때, activation function은 Sigmoid function을 사용하여 마지막 layer의 결괏값이 0부터 1 사이로 나오게 해 줍니다.

 

이를 통해서, Discriminator model은 image_size라고 하는 크기의 데이터를 받아서 해당 데이터가 만들어진 데이터인지(위조지폐인지) 혹은 실제 데이터셋에 존재하는 데이터인지(실제 지폐인지)를 판단할 수 있게 됩니다.

 

# Generator class
class Gen_model(nn.Module):
    def __init__(self, latent_space, hidden_space, image_size):
        super(Gen_model, self).__init__()
        self.features = nn.Sequential(
            nn.Linear(latent_space, hidden_space),
            nn.ReLU(),
            nn.Linear(hidden_space, hidden_space),
            nn.ReLU(),
            nn.Linear(hidden_space, image_size),
            nn.Tanh())
        
    def forward(self, input_x):
        x = self.features(input_x)
        return x

이번에는 Generator model입니다.

 

Generator model은 latent_space라는 크기의 latent variable을 입력으로 받아서 hidden_space 크기로 output을 내고, 이를 다시 hidden_space 크기로 output을 내며, 마지막으로는 image_size 만큼의 결괏값을 내보내게 됩니다.

 

이를 통해서, Generator model은 latent_space라고 하는 크기의 noise input을 받아서 image_size라고 하는 크기의 데이터를 output으로 내게 됩니다.

 

im_size = 784
hidden_size = 256
latent_size = 100

Dis_net = Dis_model(image_size = im_size, hidden_space = hidden_size).to(DEVICE)
Gen_net = Gen_model(image_size = im_size, hidden_space = hidden_size, latent_space = latent_size).to(DEVICE)

d_optimizer = optim.Adam(Dis_net.parameters(), lr = 0.0002)
g_optimizer = optim.Adam(Gen_net.parameters(), lr = 0.0002)

이미지의 사이즈는 28 * 28 이므로 784로 지정하였고, hidden layer의 차원은 256, Generator에 들어가는 latent variable의 차원은 100차원으로 지정해주었습니다.

 

이미지의 사이즈는 데이터셋에 맞춰서 설정해주시면 되고 hidden layer의 차원이나 latent variable의 차원은 유동적으로 변경하셔도 됩니다.

 

하지만 이게 너무 작거나 하게 되면 Generator나 Discriminator가 충분한 capacity를 가질 수 없을 수도 있으니 과도하게 작게 하는 것은 여러모로 안 좋게 되지 않을까 하는 생각이 듭니다.

 

Discriminator 모델은 Dis_net이라는 이름으로 설정해주고, Generator 모델은 Gen_net이라는 이름으로 설정해주었습니다.

 

만약에 GPU를 사용하시는 분이라면, 반드시 .to(DEVICE)를 지정해주셔서 이를 GPU에서 연산하도록 설정해주셔야 합니다.

 

GPU로 하는 것과 CPU로 하는 것은 딥러닝에서의 연산 시간 차이가 심합니다. 

 

그리고 Discriminator 모델과 Generator 모델을 최적화해줄 optimization algorithm으로는 Adam을 선택했습니다.

 

모델이 두 개이므로, 두 개를 따로 만들어주셔야 합니다. 

 

학습률(learning rate)도 유동적으로 선택하시면 되는데, 저는 그냥 0.0002 정도로 잡았습니다.

 

# Start training
def train(generator, discriminator, train_loader, optimizer_d, optimizer_g):

    # Train version
    generator.train()
    discriminator.train()

    for data, target in train_loader:

        data, target = data.to(DEVICE), target.to(DEVICE)

        # ==========================================#
        # ==========Optimize discriminator==========#
        # ==========================================#

        # initialize discriminator optimizer
        optimizer_d.zero_grad()

        # Make noise samples for discriminator update
        noise_samples_d = torch.randn(BATCH_SIZE, latent_size).to(DEVICE)

        # real loss
        discri_value = discriminator(data.view(-1, 28*28))
        loss_real = -1 * torch.log(discri_value) # gradient ascent

        # fake loss
        gene_value = discriminator(generator(noise_samples_d))
        loss_fake = -1 * torch.log(1.0 - gene_value) # gradient ascent

        # Final loss
        loss_d = (loss_real + loss_fake).mean()

        loss_d.backward()
        optimizer_d.step()


        # ========================================= #
        # ==========Optimize generator============= #
        # ========================================= #

        # initialize generator optimizer
        optimizer_g.zero_grad()

        # Make noise samples for generator update
        noise_samples_g = torch.randn(BATCH_SIZE, latent_size).to(DEVICE)

        # calculate loss
        fake_value = discriminator(generator(noise_samples_g))
        loss_generator = -1 * torch.log(fake_value).mean() # provide much stronger gradients early in learning.
        
        loss_generator.backward()
        optimizer_g.step()

해당 함수는 모델의 학습을 수행합니다.

 

먼저, 모델을 학습하려면 반드시 generator.train()와 같이 이 모델은 학습을 할 것이다 라는 시그널을 보내줘야 합니다.

 

반대로 학습을 하지 않고 추론만 진행하려고 한다면, .eval()를 적용해주시면 됩니다.

 

학습은 train_loader에서 데이터를 받아서 진행하므로, data와 target을 train_loader에서 전달받습니다.

 

이때, data와 target도 모델과 동일하게 .to(DEVICE)를 통해서 GPU 연산을 적용하도록 만들어줘야 합니다.

 

 

혹시나 궁금하시다면, 해당 부분에 .to(DEVICE)를 빼시면 오류가 날 겁니다. (예전에 이런 적이 있었는데, 오류명까지는 기억이 안 나고 오류 내용에 cuda 설정 어쩌고저쩌고 하면서 설명이 잘 나옵니다.)

 

먼저 optimizer_d.zero_grad()로 gradient를 초기화해주고

 

torch.randn을 이용해서 정해진 사이즈의 noise variable을 만들어줍니다. 우리는 정규분포 기준으로 만들어줍니다.

 

 

우리가 BATCH_SIZE 기준으로 데이터를 받고 연산을 진행하기 때문에, noise variable도 크기는 BATCH_SIZE에 맞춰줍니다.

 

다음으로는, 논문에 이 파트를 구현해주는 코드입니다.

 

먼저, 위 식의 첫 번째 항을 만들어줍니다.

 

discri_value는 데이터를 먼저 (200, 784) 형태로 만들어줍니다. 이는 .view()를 이용하시면 됩니다.

 

 

(200, 784)로 만들어준 실제 MNIST 데이터를 discriminator의 input으로 넣어줍니다. 

 

이렇게 하면 discriminator가 해당 데이터를 기반으로 이게 위조지폐인지 실제 지폐인지에 대한 판단을 하겠죠?

 

그 값이 바로 discri_value입니다. 

 

여기에 log 값을 취해준 게 loss_real이 되고, 실제 논문에서는 gradient ascending을 하라고 했기 때문에 여기에 -1을 곱해줘서 구현을 진행했습니다.

 

다음으로는, 두 번째 항을 만들어줍니다.

 

gene_value는 아까 만들어낸 noise sample을 generator에 넣어서 새롭게 데이터를 만들어냅니다. 

 

이를 discriminator에 넣어서 해당 데이터가 위조지폐인지 실제 지폐인지 판단한 결과 값이 gene_value입니다.

 

여기에 log 값을 취해주고, gradient ascending을 위해 -1을 곱해서 이를 loss_fake라고 지정하였습니다.

 

마지막으로, loss_real과 loss_fake를 합해주고, 이를 평균 내는 것이 논문의 내용이였으므로 .mean()을 해줍니다.

 

 

loss_d.backward()는 backpropagation을 진행하는 코드이고, optimizer_d.step()은 optimizer를 한 단계 진행해줍니다.

 

다음으로는 Generator 학습을 진행해줘야 합니다.

 

논문상으로는 해당 파트입니다.

 

 

원래는 위의 식을 사용해야 하나, 논문에서는 초기의 학습을 위해서 다음과 같이 변경하도록 하고 있습니다.

 

 

즉 $log(1-D(G(z^{(i)})))$를 최소화하는 것이 아니라, $logD(G(z))$를 최대화하는 쪽으로 학습하라는 것입니다.

 

 

동일하게, generator의 optimizer gradient를 0으로 갱신해주고

 

다시 한번 noise sample을 만들어줍니다. 이 부분은 위 식에서 $z^{(i)}$로 표현됩니다.

 

 

이를 이용해서 generator의 input으로 투입하고, 이를 다시 discriminator에 넣어서 해당 데이터가 위조지폐인지 실제 지폐인지 discriminator가 판단합니다.

 

그리고 이 값에 log을 취한 뒤에 평균을 취해주고, 최대화를 해야 하므로 여기에 -1을 곱해서 진행합니다.

 

 

마지막으로 loss_generator를 backpropagation 해주고, optimizer_g도 한 단계 진행하도록 해줍니다.

 

 

 

다음으로는 실제 학습을 진행해주는 코드를 다뤄보겠습니다.

 

for epoch in tqdm(range(EPOCHS)):
    train(Gen_net, Dis_net, trainloader, d_optimizer, g_optimizer)

    if (epoch+1)%20 == 0:
        print('epoch %i / 400' % (epoch+1))
        
        noise_sam = torch.randn(16, latent_size).to(DEVICE)
        imshow_grid(Gen_net(noise_sam).view(-1, 1, 28, 28))
        print("\n")

 

위에서 언급한 train이라는 코드가 바로 학습을 진행하는 코드이고, 여기에 Gen_net과 Dis_net, trainloader, d_optimizer, g_optimizer를 인수로 넣어서 학습을 진행해줍니다. 

 

그리고 학습이 잘 되는지를 확인해보기 위해서, 20 에폭마다 16개의 noise variable을 만들어 이를 Generator network에 통과시켜서 나오게 되는 데이터를 시각화해줍니다.

 

 

400 에폭을 학습해감에 따라서, 만들어내는 숫자들이 깔끔해지는 것을 보실 수 있습니다.

 

특히, 가장 초기 20 에폭쯤에서는 완전히 random noise 느낌의 이미지를 만들어내지만 점점 갈수록 모양을 잡아나가는 것을 볼 수 있습니다.

 

물론 아직도 원본 데이터만큼 엄청나게 좋은 데이터를 만든다고 보기는 어렵지만, 굉장히 간단한 모델과 간단한 코드를 가지고도 어느 정도의 생성 성능을 보여줄 수 있음을 확인할 수 있었습니다.

 

해당 모델은 2014년 모델로, 그 이후에 다양한 생성 모델 방법론들이 나오면서 지금은 매우 고화질의 이미지들도 만들어내긴 하지만 이렇게 단순한 코드로도 어느정도 생성을 할 수 있다는 것이 놀랍다고 생각했습니다.

 

마지막으로, 학습이 완료된 모델을 가지고 test를 진행하는 코드를 다뤄보겠습니다.

 

# For test after training
vis_loader = torch.utils.data.DataLoader(testset, 16, True)
img_vis, label_vis = next(iter(vis_loader))
imshow_grid(img_vis)

아까 만들어준 testset을 가지고 DataLoader를 만들어주고, 16개만 뽑아내 줍니다. 

 

이를 통해 맨 처음에 정의한 imshow_grid 함수를 통해 16개만 샘플로 그리드 그림을 그려줍니다.

 

# Make samples by using trained generator model.
sample_noise = torch.randn(16, latent_size).to(DEVICE)
imshow_grid(Gen_net(sample_noise).view(-1, 1, 28, 28))

 

 

16개의 sample noise를 만들어주고, 이를 400 에폭 학습이 끝난 Generator network에 투입시켜서 이미지를 생성하고 이를 (-1, 1, 28, 28) 형태로 데이터를 다시 만들어 이를 plotting 해줍니다.

 

 

물론 그림의 성능이 그렇게 썩 좋지는 않지만 그래도 나름대로 완전한 랜덤 값에서 이미지를 만들어내고 있음을 확인할 수 있었습니다.

 

 

 

여기까지 GAN 코드를 직접 짜고 돌려보면서, 정말로 이미지 생성이 잘 되는지 확인해보았습니다.

 

위에서 설명한 코드는 제 Github 주소에 있으니, 직접 돌려보고 싶은 분들은 이를 확인해주시면 되겠습니다.

 

github.com/PeterKim1/paper_code_review

 

다음에는 또 다른 논문으로 찾아오겠습니다.

 

 

Reference

 

intelligence.korea.ac.kr/members/wschoi/seminar/tutorial/mnist/pytorch/gan/GAN-%ED%8A%9C%ED%86%A0%EB%A6%AC%EC%96%BC/

 

안녕하세요.

 

 

새롭게 (paper + code) review라는 항목을 만들었고, 여기에 하나하나 글을 채워나갈 예정입니다.

 

 

블로그 글에는 논문의 내용을 조금 더 디테일하게 정리하면서 나름대로 저의 생각을 얹어서 정리할 예정이고

 

 

그와 동시에 code의 세부적인 사항들도 함께 review하면서 논문 정리 글 + 해당 논문 코드 review로 해서

 

 

논문 내용과 코드를 하나의 set로 작성하는 식의 포멧을 이용해 논문을 정리해볼 예정입니다.

 

 

그래서 게시판의 이름을 (paper + code) review 라고 짓게 되었습니다.

 

 

물론 최신 논문들을 다루는 것도 좋지만, 개인적인 생각으로는 최근 모델은 대부분 과거의 모델을 기반으로 이를 더 좋게 향상한 것이므로

 

 

오히려 뿌리, 근본에 해당하는 모델들에 대해서 디테일하게 정리를 하는 것이 중요하지 않나 라는 생각을 했습니다.

 

 

물론 너무나도 유명한 모델들은 저 또한 이 모델이 어떤 컨셉이고 어떻게 쓰이는지 등의 개략적인 내용은 알고 있지만

 

 

단순히 모델만 아는 것 외에 논문을 자세히 들여다보고 코드를 세세히 보는 것을 통해 얻을 수 있는 

 

 

또 다른 insight가 존재한다고 생각합니다. 그래서 개인적으로는 논문을 조금 디테일하게 다루는 걸 좋아하는 편이고요.

 

 

이번 글에서는 너무나도 잘 알려진 모델인 Generative Adversarial Nets(GAN)을 정리해봅니다.

 

 

아무래도 2014년에 나온 논문이고 하다 보니, 그 이전에 사용되던 모델들이 나오고 해서 모든 것을 100% 소화하기가

 

 

사실은 조금 어려운 논문이라는 생각이 들었습니다. 하지만 조금이라도 더 완벽하게 이해하려고 노력을 해봤습니다.

 

 

논문 주소: arxiv.org/abs/1406.2661

 

 

Abstract

 

 

이번 논문에서는 데이터 분포를 포착하는(capture) 생성 모델(generative model)인 $G$와 샘플이 $G$에서 나왔다기보다는 학습 데이터로부터 나왔을 가능성을 추정하는 식별 모델(discriminative model) $D$의 두 모델을 동시에 학습하는 adversarial process를 통해 생성 모델을 추정하는 새로운 framework를 제안한다.

 

$G$에 대한 학습 절차는 $D$의 확률이 실수를 만들어낼 확률을 최대화하는 것을 통해 이루어진다.

 

이러한 framework는 minimax two-player game에 대응된다. 임의의 함수 $G$와 $D$의 공간에서 유일한 해는 존재하며 이때 $G$는 학습 데이터 분포를 회복하고(recover) $D$는 모든 곳에서 $1/2$이다.

 

$G$와 $D$가 multilayer perceptron으로 정의될 때, 전체 시스템은 backpropagation을 가지고 학습될 수 있다.

 

학습할 때나 샘플을 만드는 동안에는 Markov chains이나 unrolled approximate inference network를 필요로 하지 않는다.

 

실험에서는 생성된 샘플에 대한 정량적, 정성적 평가를 통해 framework의 잠재력을 검증하였다. 

 

 

 

1. Introduction

 

 

딥러닝의 가능성은 자연스러운 이미지, speech를 포함하고 있는 오디오 파동, 자연어 말뭉치에서의 symbol과 같은 인공지능 어플리케이션에서 마주할 수 있는 다양한 데이터들에 대해서 확률 분포를 나타낼 수 있는 풍부하고 계층적인 모델을 발견하는 것이다.

 

지금까지, 딥러닝에서의 가장 현저한 성공은 discriminative model과 관련되어 있어 왔으며, 보통 고차원의, 풍부한 센서 input을 class label로 mapping 하는 모델들이다. (흔히 얘기하는 분류 모델을 생각하시면 편합니다.)

 

이러한 현저한 성공은 주로 backpropagation과 dropout 알고리즘에 기반해왔으며, 특히 잘 작동하는(well-behaved) gradient를 가지는 piecewise linear units을 사용했다. (piecewise linear unit은 구간이 나눠져 있는 선형 함수, 대표적으로 RELU와 같은 함수를 의미합니다.)

 

Deep generative models은 적은 영향력을 가지고 있었는데, 이는 최대 우도 추정(maximum likelihood estimation)과 이와 관련된 전략에서 발생하는 다루기 곤란한 확률적 computation을 근사하는 것이 어려웠기 때문이며 piecewise linear units의 이점을 generative context에서 활용하기가 어려웠기 때문이다.

 

우리는 이러한 어려움들을 회피하는 새로운 생성 모델 추정 절차를 제안한다.

 

 

제안된 adversarial nets framework에서, generative model은 적(adversary)에 대해서 pitting 된다.

 

discriminative model은 샘플이 모델 분포에서 왔는지, 혹은 데이터 분포에서 왔는지를 결정하도록 학습한다.

 

generative model은 위조지폐를 만드려고 노력하고 이를 들키지 않고 사용하는 위조범과 비슷하다고 생각되어질 수 있으며

 

discriminative model은 위조 지폐를 발견하려고 노력하는 경찰과 비슷하다.

 

이 게임에서의 경쟁은 위조범과 경찰 모두 가짜가 진짜 지폐와 구별될 수 없을 때까지 각자의 방법을 향상한다.

 

 

이 framework는 많은 종류의 모델과 최적화 알고리즘을 위한 구체적인 학습 알고리즘을 만들어낼 수 있다.

 

이번 논문에서, 우리는 generative model에 random noise를 통과시켰을 때 multilayer perceptron을 통해 샘플들을 생성해내는 특별한 케이스에 대해서 탐구하며, discriminative model 또한 multilayer perceptron이다.

 

우리는 이러한 특별 케이스를 adversarial nets라고 부른다.

 

이런 경우에, 우리는 양쪽 모델을 매우 성공적인 backpropagation과 dropout algorithm만을 사용하여 학습할 수 있으며, generative model로부터 forward propagation만 사용하여 샘플을 만들 수 있다. (forward propagation이란 한국어로는 순전파라고 부르는데, input에 어떤 것을 투입하여 layer들을 거쳐 output을 뽑아내는 것을 의미한다고 이해하시면 됩니다.)

 

approximate inference나 Markov chain이 필요하지 않다. 

 

 

 

2. Related work

 

 

잠재 변수를 이용한 directed graphical model에 대한 대안은 restricted Boltzmann machines(RBMs)나 deep Boltzmann machines (DBMs) 및 수많은 변형들과 같은 잠재 변수를 이용한 undirected graphical model이다. 

 

이러한 모델들 내에서의 상호작용은 unnormalized potential function의 곱으로 제시되며, 랜덤 변수들의 가능한 상태에 대한 전역 합이나 전역 적분에 의해서 정규화된다. (확실하진 않지만, Bayes' theorem에서 분모가 normalize 하는 역할을 해주는 것과 유사한 의미인 것 같습니다...)

 

이 양(partition function)과 이에 대한 gradient는 가장 trivial instance 외에는 모두 intractable이며, 그들은 Markov chain Monte Carlo (MCMC) method에 의해서 추정될 수 있다. Mixing은 MCMC에 의존하는 학습 알고리즘에 중요한 문제를 제기한다. 

 

 

Deep belief networks (DBNs)는 하나의 undirected layer와 여러 개의 directed layers를 포함하고 있는 하이브리드 모델이다. Fast approximate layer-wise 학습 기준이 존재하긴 하지만, DBN는 undirected model과 directed model 모두와 연관된 연산적 어려움을 초래한다. 

 

Score matching이나 noise-contrastive estimation (NCE)와 같이 log-likelihood의 한계치를 정하지 않거나 근사하지 않는 대안적 기준 또한 제안되어 왔다. 두 가지 모두 정규화 상수까지 학습된 확률 밀도를 분석적으로 지정해야 한다. 

 

DBNs나 DBMs처럼 여러 층의 잠재 변수를 가지고 있는 다양한 흥미로운 generative models에서, 계산 가능한 unnormalized 확률 밀도를 끌어내는 것은 불가능하다. 

 

Denoising auto-encoders나 contractive autoencoder와 같은 어떤 모델들은 RBMs에 적용된 score matching과 매우 유사한 학습 규칙을 가지고 있다.

 

NCE에서는, 이번 연구처럼 discriminative 학습 기준은 generative model을 fitting 하기 위해서 사용된다.

 

하지만, 별도의 discriminative model을 fitting 시키기보다는, generative model 자체가 고정된 노이즈 분포로부터 나온 샘플을 구별하는 데 사용된다.

 

NCE는 고정된 노이즈 분포를 사용하기 때문에, 모델이 관측 변수의 작은 부분 집합에 대해 근사적으로 올바른 분포를 학습한 후에는 학습 속도가 크게 느려진다.

 

 

마지막으로, 몇몇 기법들은 확률 분포를 명시적으로 정의하는 것을 포함하는 게 아니라 오히려 희망하는 분포로부터 샘플을 뽑기 위해 generative machine을 학습시킨다. 

 

이 접근법은 이러한 machine들이 backpropagation에 의해서 학습되도록 설계될 수 있다는 이점을 가지고 있다.

 

이러한 분야에서의 저명한 최근 연구는 generative stochastic network (GSN) framework를 포함하며, 이는 generalized denoising auto-encoder를 확장하는 것이다.

 

둘 다 parameterized Markov chain을 정의하는 것으로 볼 수 있으며, 이는 즉 generative Markov chain의 한 단계를 수행하는 machine의 파라미터들을 학습한다.

 

GSNs와 비교했을 때, adversarial nets framework는 샘플링을 위해 Markov chain을 필요로 하지 않는다.

 

Adversarial nets가 생성하는 동안에 feedback loop를 필요로 하지 않기 때문에, 이들은 더더욱 piecewise linear units을 더 잘 활용할 수 있으며 이는 backpropagation의 성능을 향상하지만 feedback loop 안에서 사용되었을 때는 unbounded activation의 문제점을 가지게 된다.

 

Back-propagation을 이용해서 generative machine을 학습시키는 더 최근의 예시들은 auto-encoding variational Bayes와 stochastic backpropagation의 최근 연구들을 포함한다.

 

(개인적인 생각으로는, 워낙 예전 모델들에 대한 설명이라서 모든 걸 다 이해하기는 어려운 것 같습니다. )

 

 

 

3. Adversarial nets

 

 

Adversarial modeling framework는 모델들이 둘 다 multilayer perceptron이면 적용하기에 더욱 직관적이다.

 

Generator의 분포 $p_g$를 데이터 $x$에 대해서 학습하기 위해서, input noise variables $p_z(z)$에 prior를 정의하고 data space로의 mapping을 $G(z; \theta_g)$로 표현하며 $G$는 parameter $\theta_g$를 가지는 multilayer perceptron으로 표현되는 미분 가능한 함수이다.

 

그다음으로 single scalar를 결과로 내는 두 번째 multilayer perceptron $D(x; \theta_d)$를 정의한다.

 

$D(x)$는 $x$가 $p_g$보다 data로부터 나왔을 가능성을 나타낸다.

 

우리는 $D$를 training examples와 $G$로부터 나온 샘플 모두에게 올바른 label을 할당할 확률을 최대화하기 위해 훈련한다.

 

동시에 $G$가 $log(1-D(G(z)))$를 최소화하도록 학습한다.

 

다시 말해서, $D$와 $G$는 다음의 two-player minimax game을 가치 함수 $V(G, D)$를 가지고 진행하게 된다.

 

 

다음 논문의 내용을 전개하기 전에, 먼저 GAN의 가치 함수 $V(D, G)$에 대해서 정리를 하고 넘어가겠습니다.

 

결국 이 가치 함수가 $D$와 $G$ 관점에서 지향하는 방향성이 무엇인지를 파악하는 것이 해당 논문의 가장 핵심이라고 생각합니다.

 

먼저 $G$ 관점에서 살펴보겠습니다.

 

$G$ 관점에서는 해당 가치 함수를 minimize 하는 것이 목표이며, Equation 1에서 존재하는 두 항 중에서 실제로 $G$와 관련이 있는 항은 두 번째 항이므로, 두 번째 항을 통해서 $G$가 지향하는 목표가 무엇인지 확인해보겠습니다.

 

 

먼저, $E$의 아래 첨자로 들어가는 $z$는 noise입니다. $E$를 표시했으므로, noise 분포인 $p_z(z)$에서 나온 noise $z$에 대해서 해당 값의 기댓값을 계산하겠다는 의미입니다.

 

다음으로, log 안쪽의 식을 보겠습니다.

 

$log(1-D(G(z)))$라고 적혀 있는데, $D(G(z))$를 $x$로 치환한다고 하면 결국 이 식은 $log(1-x)$가 되는 것이죠?

 

즉 $log(1-x)$를 최소화하는 것이 목표라는 것입니다. $log(1-x)$라고 했을 때 바로 그래프가 떠오르시는 분도 계시겠지만, 기억이 안 날 수 있으니 그래프를 들고 와 보겠습니다.

 

 

해당 그래프에서 함숫값이 가장 작아지려면 어떻게 되어야 할까요?

 

$x$가 1에 가까워지면 함숫값이 매우 작아지게 됩니다. 즉, $D(G(z))$가 1이 되어야 합니다.

 

$D(x)$는 앞에서도 언급했지만, $D(x)$는 $x$가 $p_g$보다 data로부터 나왔을 가능성을 나타냅니다.

 

즉, $D(G(z))$는 noise $z$를 입력으로 받아서 $G$를 통해 나오게 된 결과를 입력으로 받았을 때, 이것이 $p_g$보다 data로부터 나왔을 가능성을 나타냅니다.

 

$D(G(z))$가 1이 된다는 것은, $D$가 해당 데이터를 data로부터 나왔다고 판단할 수 있을 정도로 $G$가 정말 감쪽같은 결과를 만드는 것을 의미합니다. 

 

맨 처음의 예시에서 $G$는 위조지폐범이였고, $D$는 위조지폐를 발견하려고 노력하는 경찰이라고 비유했었는데 $D(G(z))$가 1이 된다는 것은 경찰이 완전히 속을 정도로 위조 지폐범이 완벽한 위조 지폐를 만들었음을 의미합니다.

 

 

다음으로는 $D$ 관점에서 보겠습니다.

 

$D$는 가치 함수 $V(D, G)$의 두 항에 모두 포함되어 있으므로, 두 항을 모두 살펴보겠습니다.

 

$D$는 가치 함수 $V(D, G)$를 최대화하는 것을 목표로 하고 있으며, 두 항의 합이 최대가 되려면 결국 각 항들이 최댓값을 가져야 합니다.

 

방금 봤었던 두 번째 항을 먼저 살펴보겠습니다.

 

 

$log(1-D(G(z)))$에서 $D(G(z))$를 $x$로 치환한다면, 아까와 동일하게 결국 $log(1-x)$를 다루는 문제가 됩니다.

 

따라서, $D$ 입장에서는 해당 식을 최대로 하고 싶어 합니다.

 

그렇다면 어떻게 해야 $log(1-x)$가 최댓값을 갖게 될까요? 당연히 $x$의 값을 최대한으로 낮춰주면 됩니다. (위의 그래프 참고)

 

하지만, $x$는 $D(G(z))$로, 어떤 input값이 어떤 분포로부터 나왔는지를 판단한 값으로, 해당 값은 0부터 1 사이의 값을 갖게 됩니다. 따라서, $log(1-x)$의 그래프에서 정의역이 [0, 1]인 상황을 생각해야 된다는 것이죠.

 

이렇게 된다면, $x$가 0이 되었을 때, $log(1-x)$가 최댓값을 갖게 되며 이는 $D(G(z))$가 0이 되는 것을 의미합니다.

 

$D(G(z))$가 0이 된다는 것은, noise $z$를 입력으로 받아서 $G$가 만들어낸 결과를 $D$ 입장에서 판단했을 때 이것이 $p_g$에서 나왔다고 정확하게 판단함을 의미합니다.

 

앞의 비유를 가지고 생각해보자면, 위조지폐범이 만들어낸 위조지폐를 보고 경찰이 이것은 100%로 위조지폐다!라고 완벽하게 판단하는 경우를 의미합니다. 

 

다음으로는, 가치 함수의 첫 번째 항을 살펴보겠습니다.

 

 

$E$의 아래 첨자로 들어간 $x$는 우리가 가지고 있는 실제 데이터를 의미합니다.

 

다음으로, 최대로 만들고 싶은 식이 바로 $logD(x)$인데요, 이번에는 $logx$ 그래프를 보겠습니다.

 

 

아까 얘기했지만, $D(x)$ 값은 [0, 1]에서 값을 갖게 됩니다. 따라서, $logx$ 그래프에서 정의역이 [0, 1]인 경우를 의미하는 것이죠.

 

이는 $x$가 1일 때 최댓값을 가지게 되며, 이는 $D(x)$가 1이 됨을 의미합니다.

 

앞의 비유를 이용해서 설명해보자면, 실제 지폐를 보고 경찰이 정확하게 이 지폐가 실제 지폐임을 알아맞히는 것을 의미하는 것이죠.

 

 

지금까지 설명한 내용을 정리하자면, 가치 함수를 통해서 알 수 있는 사실은

 

$G$의 목표는 위조지폐를 감별하는 경찰이 못 맞출 정도로 매우 정교한 위조 지폐를 만들어내는 것을 목표로 한다.

 

즉, $D(G(z))$가 1이 되도록 학습하는 것이 $G$의 목표가 된다.

 

$D$의 목표는 위조지폐는 위조지폐라고 감별하고, 실제 지폐는 실제 지폐라고 정확히 분류하는 것을 목표로 한다.

 

즉, $D(x)$는 1이 되도록, $D(G(z))$는 0이 되도록 학습하는 것이 $D$의 목표가 된다.

 

 

 

다음 section에서는 adversarial nets에 대한 이론적인 분석을 제시하며, 기본적으로 non-parametric limit에서 $G$와 $D$가 충분한 capacity를 제공받기 때문에 학습 기준이 adversarial nets가 data generating distribution을 복구하도록 허용함을 보여준다.

 

해당 접근법에 대한 덜 공식적이지만 더욱 교육학적인 설명인 Figure 1을 참고하자.

 

실제로, 우리는 이 게임을 반복적이고 수학적인 접근법을 사용하여 실행해야 한다. 

 

$D$를 학습 내부 loop에서 완성에 가까이 최적화하는 것이 computationally prohibitive 하며, 유한한 데이터셋에서는 과적합을 야기하게 된다.

 

그 대신에, 우리는 $D$를 최적화하는 $k$단계와 $G$를 최적화하는 1단계를 번갈아 진행한다.

 

이는 $D$가 이것의 최적해 근처에 있도록 유지되는 결과를 만들며, 그동안 $G$는 충분히 느리게 변화한다.

 

이러한 전략은 학습의 내부 loop의 일부분으로써 Markov chain에서 burning 하는 것을 회피하기 위해 SML/PCD 학습이 one learning step에서부터 다음 learning step까지 Markov chain으로부터의 샘플을 유지하는 방법과 유사하다. (아무리 봐도 여기서 burning의 의미를 알 수가 없네요...)

 

해당 절차는 Algorithm 1에 나와있다.

 

 

실제로, Equation 1은 아마 $G$가 잘 학습하기 위해 충분한 gradient를 제공하지 못한다.

 

학습 초기에, $G$가 잘 못할 때, 생성된 샘플들이 training data와 분명하게 다르기 때문에 $D$는 높은 confidence로 샘플들을 거절할 수 있다.

 

이러한 경우에, $log(1-D(G(z)))$는 saturate 된다. 

 

$log(1-D(G(z)))$를 최소화하기 위해 $G$를 학습하는 것 대신에, $logD(G(z))$를 최대화하도록 $G$를 학습할 수 있다. 

 

이러한 목적 함수는 $G$와 $D$의 dynamics의 동일한 고정된 지점의 결과를 낳지만, 학습 초기에 더욱 강력한 gradient를 제공한다.

 

 

 

위 단락에서 설명한 내용은 다음과 같은 그림으로 이해해볼 수 있습니다.

 

 

학습 초기에는, $G$가 누가 봐도 위조지폐처럼 생긴 샘플들을 만들기 때문에 $D(G(z))$가 매우 작은 값이 나오게 됩니다.

 

따라서, 기존 가치 함수처럼 $log(1-D(G(z)))$를 최소화하도록 한다고 가정하면 오른쪽에 있는 그림처럼 Gradient의 값이 매우 작은 값을 갖게 됩니다. (접선의 기울기가 gradient라고 생각해주시면 이 값이 매우 작음을 알 수 있습니다. 해당 그래프에서의 $x$는 $D(G(z))$이며, 이 값이 0.1라고 생각하고 접선을 오른쪽과 왼쪽 그래프에 만들었습니다.)

 

하지만 이를 $log(D(G(z)))$를 최대화하는 것으로 만들게 되면, 왼쪽 그림에서 보이듯이 $D(G(z))$가 작은 값을 가질 때도 Gradient의 값이 매우 큰 값을 가지는 것을 알 수 있습니다.

 

이러한 방법을 통해 $G$가 학습 초기 단계에서 좋지 못한 샘플을 만들 때도 원활하게 학습이 이루어질 수 있도록 할 수 있습니다.

 

 

 

위의 Figure 1은 Generative adversarial nets가 학습되는 과정을 나타내고 있습니다.

 

Generative adversarial nets는 데이터 생성 분포(검은색 점선) $p_x$에서 나온 샘플을 generative distribution $p_g(G)$ (녹색 실선)에서 나온 샘플로부터 구별하기 위해 discriminative distribution($D$, 파란색 선)을 동시에 업데이트시키면서 학습하게 된다.

 

아래쪽 수평선은 $z$가 샘플링된 domain이며, 이 경우에서는 uniform이다.

 

위쪽 수평선은 $x$ domain의 일부이다. 

 

위쪽을 향한 화살표들은 어떻게 mapping $x = G(z)$가 non-uniform distribution $p_g$를 변형된 샘플에 도입하는지를 나타낸다.

 

$G$는 $p_g$의 높은 밀도의 영역에서 수축하고 $p_g$의 낮은 밀도의 영역에서 확장된다.

 

(a) adversarial pair가 수렴에 가까워졌다고 생각하자. 이때, $p_g$는 $p_{data}$과 유사하며 $D$는 부분적으로 정확한 분류기이다. ($G$가 아직 실제 데이터 분포와 많이 다르고, discriminative distribution도 아직은 많이 부정확한 상태)

 

(b) algorithm의 inner loop에서 $D$는 데이터로부터의 샘플을 구별하도록 학습되며, $D^*(x) = \frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$에 수렴한다.  ($D$는 정확하게 분류할 수 있는 최적의 분류기가 된 상태)

 

(c) $G$가 업데이트된 후, $D$의 gradient는 $G(z)$가 데이터로 분류될 가능성이 더욱 높은 지역으로 흘러가도록 안내한다. ($G$가 점점 실제 데이터 분포에 가까워지고 있는 상태)

 

(d) 여러 단계의 학습 후에, $G$와 $D$가 충분한 용량을 가진다면, 이들은 더욱 향상될 수 없는 지점에 도달하게 되는데 이는 $p_g = p_{data}$이기 때문이다. Discriminator는 두 분포 사이를 구분할 수 없게 되며 즉, $D(x) = \frac {1}{2}$가 된다. ($G$가 실제 지폐와 거의 똑같은 위조지폐를 만들게 되어 경찰이 위조지폐와 실제 지폐를 구분할 수 없는 상태가 되어버림.)

 

 

 

4. Theoretical Results

 

 

 

Generator $G$는 $z$가 $p_z$에서 얻어졌을 때 샘플 $G(z)$의 분포로써 확률 분포 $p_g$를 암시적으로 정의한다.

 

그러므로, 충분한 capacity와 학습 시간이 주어졌을 때 Algorithm 1이 $p_{data}$의 좋은 estimator로 수렴하기를 원한다.

 

이번 section의 결과는 non-parametric setting으로 이루어졌으며, 이는 확률 밀도 함수의 공간에서 수렴을 학습하는 과정을 통해 무한한 capacity를 가지는 모델을 표현한다는 의미이다.

 

section 4.1에서는 해당 minimax game이 global optimum을 $p_g = p_{data}$에서 가짐을 보일 것이다.

 

다음으로 section 4.2에서는 Algorithm 1이 Equation 1을 최적화하여 원하는 결과를 얻음을 보일 것이다.

 

 

Algorithm 1은 adversarial nets의 minibatch stochastic gradient descent training을 나타내고 있다. Discriminator에 적용되는 step의 수인 $k$는 hyperparameter이다. 실제 실험에서는 실험에서 가장 저렴한 option인 $k$ = 1로 설정하였다. (연산량 관점에서 가장 부담이 없다는 의미라고 보시면 됩니다.)

 

해당 알고리즘은 크게 두 부분으로 나눠져 있는데, 가볍게 짚고 넘어가 보겠습니다.

 

 

첫 번째 단계는 noise prior $p_g(z)$에서 $m$개의 샘플을, 데이터 생성 분포 $p_{data}(x)$에서 $m$개의 샘플을 추출하여 이전에 논의해본 가치 함수를 discriminator 관점에서 최대화하는 방향으로 업데이트합니다.

 

일반적으로 딥러닝 library들은 Gradient Descent를 지원하기 때문에, 실제 코드에서 구현할 때는 해당 가치 함수에 음수를 취하여 Gradient Descent를 적용하면 결론적으로는 Gradient Ascent를 구현할 수 있을 것입니다.

 

앞에서 언급했지만, discriminator의 목표는 실제 지폐를 실제 지폐로 정확히 분류하고, 위조지폐를 위조지폐로 정확히 분류하는 것을 목표로 합니다.

 

여기서는 $k$ step 동안 진행하도록 for문으로 구성되어 있는데, 실제 실험에서는 $k = 1$로 진행했다고 합니다.

 

 

두 번째 단계는 noise prior $p_g(z)$에서 $m$개의 noise sample을 샘플링해서 이를 통해 generator를 업데이트하는 과정입니다.

 

Generator는 해당 식을 최소화 하는 것을 목표로 하기 때문에, gradient descent를 그대로 진행해주면 됩니다.

 

앞에서 언급했지만, Generator는 경찰이 구별하기 어려울 정도로 정교한 위조지폐를 만드는 것을 목표로 합니다.

 

 

 

4.1 Global Optimality of $p_g = p_{data}$

 

 

 

주어진 generator $G$에 대해서 최적의 discriminator $D$를 먼저 고려해보자.

 

Proposition 1. $G$가 고정되어 있을 때, 최적의 discriminator $D$는 다음과 같다.

 

 

Proof. 어떤 generator $G$가 주어졌을 때 Discriminator $D$에 대한 학습 기준은 $V(G, D)$를 최대화하는 것이다.

 

 

(앞에서 언급되었던 $V(G, D)$와 모양이 살짝 다른데, 이는 Expectation 형태로 되어 있던 식을 integral 형태로 변환한 것입니다. 따라서, 식의 모양만 달라진 것이라고 보시면 되겠습니다.)

 

(첫 번째 줄의 두 번째 항이 두 번째 줄로 넘어가는 이유는, 어떤 generator $G$가 주어졌다고 가정하기 때문에 $z$를 $x$로 변환했다고 생각하시면 되겠습니다.)

 

(0, 0)이 아닌 $(a, b) \in R^2$에 대해서, 함수 $y -> alog(y) + blog(1-y)$는 [0, 1]에서 $\frac{a}{a+b}$에서 최댓값을 갖게 된다. Discriminator는 $Supp(p_{data}) \cup Supp(p_g)$의 외부에서 정의될 필요가 없다.

 

(여기서 Supp은 한국어로 지지 집합이라는 개념인데, 함수값이 0이 되지 않는 점들의 집합정도로 이해하면 되는 것 같습니다. (a, b)가 (0, 0)이 아니라고 했기 때문에, 지지집합 외부에서 따로 정의할 필요가 없다고 말하는 것 같습니다.

함수 $y -> alog(y) + blog(1-y)$가 갑자기 나온 이유는, 위의 (3) 식에서 $p_{data}(x)log(D(x)) + p_g(x)log(1-D(x))$를 이와 같은 형태로 만들 수 있기 때문입니다. 즉, $a = p_{data}(x), y = D(x), b = p_g(x)$로 치환하면 형태가 딱 맞습니다.

$alog(y) + blog(1-y)$를 $y$에 대해서 미분해보시면, $\frac{a}{a+b}$에서 최댓값을 가짐을 확인할 수 있습니다.)

 

 

$D$에 대한 학습 목적 함수는 $Y$가 나타내는 것이 $x$가 $p_{data}$로부터 왔는지($y=1$) 아니면 $p_g$에서 왔는지($y=0$)일 때, 조건부 확률 $P(Y = y | x)$을 추정하는          log-likelihood를 최대화하는 것으로 해석될 수 있다.

 

Equation 1에서의 minimax game은 다음과 같이 다시 쓰일 수 있다.

 

 

Theorem 1. 가상의 학습 기준 $C(G)$의 전역 최솟값은 $p_g = p_{data}$일 때 얻어질 수 있다. 해당 지점에서, $C(G)$는 $-log4$의 값을 가진다.

 

Proof. $p_g = p_{data}$일 때, $D^*_G(x) = \frac{1}{2}$이다. (Equation 2.를 고려해보자.) 이러한 이유로, $D^*_G(x) = \frac{1}{2}$에서 Eq.4를 확인해봤을 때, $C(G) = log(1/2) + log(1/2) = -log4$임을 알 수 있다. 이 값이 $C(G)$의 가능한 가장 좋은 값임을 확인하기 위해서, $p_g = p_{data}$에 도달했을 때 다음을 확인할 수 있다.

 

 

그리고 $C(G) = V(D^*_G, G)$에서 해당 식을 뺐을 때, 다음을 얻게 된다.

 

 

 

중간 과정이 다 빠진 상태로 바로 (5) 식이 나오게 되는데, 이 과정을 조금 더 상세하게 적어드리겠습니다.

 

 

처음 줄은 (4)의 가장 마지막 줄의 식부터 시작합니다. $E$ 형식으로 적힌 식을 먼저 integral 형태로 변환해줍니다.

 

다음으로는, 식에 log4를 빼주고, 원래 식과 동일해야 하므로 다시 log4을 더해줍니다.

 

$log4$ = $2log2$ 이므로 이와 같이 표시해줬으며, 그다음 줄에서는 $log2$를 각 integral 식에 분배해줘서 integral 식에 log 2가 하나씩 들어갔습니다. log에서의 합은 안에서의 곱이 되므로, 2 * $p_{data}(x)$와 2 * $p_g(x)$가 된 것이라고 보시면 되겠습니다.

 

그다음으로는 KL이라는 식이 나오게 되는데, 이는 Kullback-Leibler divergence라는 것으로 두 분포의 차이를 나타낼 때 사용됩니다. $KL(p \parallel q)$ = $\int_x plog \frac{p}{q} dx$가 성립합니다. 따라서 (5) 식 상세 과정의 마지막 두 번째 줄에서 KL로 표시가 된 것이라고 보시면 됩니다. KL divergence까지 다루면 글이 너무 길어질 것 같아, KL divergence에 대한 상세한 내용은 생략하겠습니다.

 

이 식을 다시 한번 정리해서 Jensen-Shannon divergence로 바꿀 수 있습니다.

 

 

JSD는 Jensen-Shannon divergence인데, 이는 다음을 만족합니다.

 

 

따라서, $2 * JSD(p_{data} \parallel p_g)$로 표현될 수 있는 것입니다.

 

 

두 분포 사이의 JSD는 항상 non-negative이며 두 분포가 동일할 때만 0이므로, $C^* = -log4$가 $C(G)$의 전역 최솟값임을 알 수 있다. 이때 유일해는 $p_g = p_{data}$이다. 즉, 생성 모델이 데이터 생성 과정을 완벽하게 복제하는 상황이다.

 

 

 

4.2 Convergence of Algorithm 1

 

 

 

Proposition 2. $G$와 $D$가 충분한 capacity를 가진다면, 그리고 Algorithm 1의 각 단계에서, discriminator는 $G$가 주어졌을 때 discriminator의 최적 값에 도달하도록 허용되며, 해당 기준을 향상하기 위해 $p_g$는 업데이트된다.

 

 

그러고 나서 $p_g$는 $p_{data}$에 수렴한다.

 

 

Proof. $V(G, D) = U(p_g, D)$가 위의 기준에서 이루어지는 $p_g$의 함수라고 하자. $U(p_g, D)$는 $p_g$에서 convex이다. Convex function의 상한에 대한 하위 미분은 최댓값이 얻어지는 지점에서의 함수의 미분 값을 포함한다.

 

다르게 얘기해서, 만약 $f(x) = sup_{a \in A} f_\alpha(x)$이고 $f_\alpha (x)$가 모든 $\alpha$에 대해서 $x$에서 convex라면, $\beta = argsup_{a \in A} f_\alpha (x)$일 때 $\partial f_\beta(x) \in \partial f$이다. 

 

이는 최적의 $D$에서 이와 대응되는 $G$가 주어졌을 때 $p_g$에 대해 gradient descent update를 계산하는 것과 동일하다.

 

$sup_D U(p_g, D)$는 Theorem 1에서 증명된 것처럼 유일한 전역 최적 값을 가질 때 $p_g$에서 convex이며, 그러므로 $p_g$의 충분히 작은 업데이트만을 가지고도 $p_g$는 $p_x$에 수렴할 수 있다.

 

(위의 내용이 워낙 수학적인 내용이 많아, 100% 이해를 할 수는 없었지만 대략 우리가 생각하는 가치 함수인 $V(G, D)$가 $p_g$의 함수이며 convex 함수이기 때문에 gradient descent update를 계산하는 것과 동일한 과정을 통해서 결국 몇 번의 업데이트를 통해 $p_g$가 최적 값인 $p_x$에 수렴할 수 있다는 그런 내용으로 보입니다.)

 

실제로, adversarial nets은 함수 $G(z;\theta_g)$를 통해서 $p_g$ 분포의 제한된 부분만 표현할 수 있으며, 따라서 $p_g$ 자체를 최적화하기보다는 $\theta_g$를 최적화한다.

 

$G$를 정의하기 위해서 multilayer perceptron을 사용하는 것은 parameter 공간에서 여러 개의 중요한 문제들을 만든다.

 

하지만, 실전에서 multilayer perceptron가 훌륭한 성능을 가지고 있기 때문에 그들의 이론적 보증이 부족함에도 불구하고 이를 사용하는 것이 합리적이다.

 

 

 

5. Experiments

 

 

 

MNIST, Toronto Face Database (TFD), CIFAR-10을 포함하는 여러 개의 데이터셋에 adversarial nets을 학습시켰다.

 

Generator nets는 RELU와 sigmoid activation을 사용하였으며, discriminator net은 maxout activation을 사용하였다.

 

Dropout은 discriminator net을 학습할 때 적용되었다.

 

비록 우리의 이론적인 framework가 dropout의 사용과 generator의 중간 layer에서의 다른 노이즈를 허용하지만, generator network의 맨 아래 layer의 input으로만 노이즈를 사용했다.

 

 

Gaussian Parzen window를 $G$에 의해 생성된 샘플에 fitting 하고, 이 분포 하에서 log-likelihood를 보고하는 것을 통해 $p_g$하에서의 test set data의 확률을 추정하였다. 

 

Gaussian의 $\sigma$ parameter는 validation set에 cross validation을 통해 얻었다.

 

이 절차는 Breuleux et al.에 의해 도입되었으며, 정확한 가능도를 계산할 수 없는 여러 가지 생성 모델에 대해서 사용되었다.

 

결과는 Table 1에 나타나 있다.

 

가능도를 추정하는 이 방식은 어쨌든 높은 분산을 가지고 있으며, 고차원 공간에서 잘 작동하지 않으나 현재 우리 지식에서는 최선의 방법이다.

 

샘플링은 할 수 있지만 가능도를 직접적으로 추정할 수 없는 생성 모델에서의 진보는 어떻게 이러한 모델들을 평가할 수 있는지에 대한 추후 연구에 동기부여를 제공한다.

 

(아마 이 시기에는 생성 모델들이 많지 않아서 어떤 기준으로 평가해야 되는지 몰라 이러한 방식으로 평가한 것 같습니다.)

 

 

Figure 2와 3에서는 학습이 끝난 후의 generator net에서 나온 샘플을 보여준다. 

 

우리가 기존 방법들에 의해서 만들어진 샘플보다 여기 나온 샘플들이 더 좋다고 단언할 수는 없지만, 여기 나온 샘플들이 다른 연구에서 나타나는 더 좋은 생성 모델과 적어도 경쟁할 수 있으며 adversarial framework의 잠재력을 강조할 수 있을 것이라고 생각한다.

 

 

 

 

6. Advantages and disadvantages 

 

 

 

우리가 제안하는 새로운 framework는 기존의 modeling framework와 비교했을 때 유리한 점과 불리한 점이 존재한다.

 

불리한 점들은 주로 $p_g(x)$에 대한 명시적인 representation이 없다는 것이며, 학습하는 동안에 $D$가 반드시 $G$와 동시에 움직여야 한다는 점이다. (특히, $G$는 $D$가 업데이트되는 것 없이 너무 많이 학습되어서는 안 되며, 이는 $G$가 너무 많은 $z$값들을 같은 값의 $x$로 붕괴(collapse)되는 "Helvetica scenario"를 피하고 모델이 충분한 다양성을 가지도록 하기 위함이다.)  => 일반적으로 'Mode collapse'라고 하는 현상을 이렇게 부르는 것 같습니다. 즉 Generator가 다양한 모습을 만들어내지 못하는 상황을 의미하는 것 같습니다.

 

이는 Boltzmann machine의 negative chain이 학습 단계 동안에 반드시 최신으로 유지되어야 하는 것과 같다.

 

유리한 점은 Markov chains이 결코 필요하지 않다는 점이며, gradient를 얻기 위해 오직 backpropagation만 사용되고 학습 동안에 inference가 필요하지 않으며 매우 다양한 함수들이 모델에 포함될 수 있다.

 

Table 2는 다른 생성 모델 접근법들과 generative adversarial nets와의 비교를 요약한다.

 

 

앞에서 서술한 유리한 점은 주로 연산적인 부분이다. Adversarial model들은 또한 데이터 예시를 통해 직접적으로 generator network를 업데이트해주지 않아도 된다는 점에서 어떠한 통계적 이점을 얻을 수 있으며, 또한 gradient가 discriminator를 통해서 흐른다는 이점이 있다.

 

이는 input의 요소들이 직접 generator의 parameter들로 복사되지 않는다는 것을 의미한다.

 

Adversarial networks의 또 다른 이점은 이들이 매우 날카롭고 심지어 퇴보적인 분포를 나타낼 수 있지만, Markov chains를 기반으로 하는 방법들은 체인이 모드 간에 혼합이 될 수 있도록 분포가 다소 blurry 해야 함을 필요로 한다.

 

 

 

7. Conclusions and future work

 

 

해당 framework는 많은 단순한 확장이 가능하다.

 

 

1. 조건부 생성 모델(conditional generative model) $p(x | c)$를 $G$와 $D$에 $c$를 input으로 추가함으로써 얻을 수 있다.

 

2. $x$가 주어졌을 때 $z$를 예측하는 보조적인 네트워크를 학습하는 것을 통해 Learned approximate inference가 수행될 수 있다.

 

이는 wake-sleep algorithm으로 학습된 inference net과 유사하지만, generator net가 학습을 끝낸 후 고정된 generator net에 대해서 inference net을 학습시킬 수 있다는 이점이 있다.

 

3. 파라미터들을 공유하는 조건부 모델들의 family를 학습시키는 것을 통해 $S$가 $x$의 인덱스의 부분집합일 때 해당 모델은 모든 조건부 확률

을 근사적으로 모델링할 수 있다. (아무리 찾아봐도 저 표기를 직접 타이핑할 수 없어서 그림으로 대체합니다.)

 

본질적으로, deterministic MP-DBM의 stochastic exntension을 실행하기 위해서 adversarial nets을 사용할 수 있다.

 

4. Semi-supervised learning: discriminator나 inference net의 features는 제한된 labeled data만 이용 가능할 때 classifier의 성능을 향상할 수 있다.

 

5. Efficiency improvements: $G$와 $D$를 조정하기 위한 더 나은 방법을 분할하거나, 훈련 중에 샘플 $z$에 대한 더 나은 분포를 결정한다면 학습이 크게 가속화될 수 있다. (Generator와 Discriminator를 학습하는 방법을 개발하거나, 혹은 $z$에 대한 prior 분포를 다르게 결정하면 학습에 도움이 될 수 있다는 말인 것 같습니다.)

 

이번 논문은 adversarial modeling framework의 실행 가능성을 검증하였으며, 이러한 연구 방향이 유용하다는 것을 검증할 수 있다고 주장한다.

 

 

 

드디어 논문의 내용을 모두 다뤄보았습니다.

 

일부 내용들은 심도 있게 다루지 않았음에도 생각보다 작성하는데 들어가는 시간이 꽤 오래 걸리네요.

 

다음 글에서는 해당 논문을 코드로 어떻게 구현할 수 있는지를 살펴보겠습니다.